
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
Метод золотого сечения
Как известно, золотым сечением отрезка называется деление отрезка на две неравные части так, чтобы отношение длины всего отрезка к длине большей части равнялось отношению длины большей части к длине меньшей части отрезка. Легко показать, что золотое сечение отрезка производится двумя точками y и z, симметричными относительно середины отрезка, т.е. золотое сечение должно обладать следующими свойствами: 1) Если количество пробных точек принимается равным двум, то их следует размещать на одинаковых расстояниях от середины интервала.
2) Пробные точки должны размещаться в интервале по симметричной схеме таким образом, чтобы отношение длины исключаемого подынтервала к величине интервала поиска оставалось постоянным.
3) На каждой итерации процедуры поиска должно вычисляться только одно значение функции в получаемой точке.
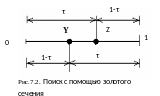
Руководствуясь
этими требованиями (1-3), рассмотрим
симметричное расположение двух пробных
точек на исходном интервале единичной
длины, которое показано на рисунке 7.2.
(Выбор единичного интервала обусловлен
соображениями удобства). Пробные точки
отстоят от граничных точек интервала
на расстоянии
![]() .
При таком симметричном расположении
точек длина остающегося после исключения
интервала всегда равна
независимо от того, какое из значений
функции в пробных точках оказывается
лучшим. Предположим, что исключается
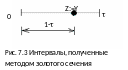
правый подынтервал. На рисунке 7.3
показано, что оставшийся подынтервал
длины
содержит одну пробную точку, расположенную
на расстоянии
.
При таком симметричном расположении
точек длина остающегося после исключения
интервала всегда равна
независимо от того, какое из значений
функции в пробных точках оказывается
лучшим. Предположим, что исключается
правый подынтервал. На рисунке 7.3
показано, что оставшийся подынтервал
длины
содержит одну пробную точку, расположенную
на расстоянии
![]() от
левой граничной точки. Для того чтобы
симметрия поискового образца сохранялась,
расстояние
должно
составлять
-ю
часть длины интервала (которая равна
).
При таком выборе
следующая пробная точка размещается
на расстоянии, равной
-й
части длины интервала, от правой граничной
точки интервала (рис. 7.4).
от
левой граничной точки. Для того чтобы
симметрия поискового образца сохранялась,
расстояние
должно
составлять
-ю
часть длины интервала (которая равна
).
При таком выборе
следующая пробная точка размещается
на расстоянии, равной
-й
части длины интервала, от правой граничной
точки интервала (рис. 7.4).
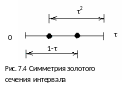
Величину выбираем из условия - отношение длины исключаемого подынтервала к величине интервала поиска оставалось постоянным.
![]() (7.2)
(7.2)
Отсюда
следует, что при выборе
в соответствии с условием
![]() симметрия
поискового образца, показанного на
рисунке 7.2, сохраняется при переходе к
уменьшенному интервалу, который изображен
на рисунке 7.4. Решая это квадратное
уравнение, получаем
симметрия
поискового образца, показанного на
рисунке 7.2, сохраняется при переходе к
уменьшенному интервалу, который изображен
на рисунке 7.4. Решая это квадратное
уравнение, получаем
![]() (7.3)
(7.3)
откуда
положительное решение
![]() .
Схема поиска, при которой пробные точки
делят интервал в этом отношении, известна
под названием поиска
с помощью метода золотого сечения.
Заметим, что после первых двух вычислений
значений функции каждое последующее
вычисление позволяет исключить
подынтервал, величина которого составляет
-ю
долю от длины интервала поиска.
Следовательно, если исходный интервал
имеет единичную длину, то величина
интервала, полученного в результате N
вычислений значений функции, равна
.
Схема поиска, при которой пробные точки
делят интервал в этом отношении, известна
под названием поиска
с помощью метода золотого сечения.
Заметим, что после первых двух вычислений
значений функции каждое последующее
вычисление позволяет исключить
подынтервал, величина которого составляет
-ю
долю от длины интервала поиска.
Следовательно, если исходный интервал
имеет единичную длину, то величина
интервала, полученного в результате N
вычислений значений функции, равна
![]() .
Можно показать, что поиск с помощью
метода золотого сечения является
асимптотически наиболее эффективным
способом реализации минимаксной
стратегии поиска.
.
Можно показать, что поиск с помощью
метода золотого сечения является
асимптотически наиболее эффективным
способом реализации минимаксной
стратегии поиска.
В общем случае отрезка [a,b]
![]()
![]()
Нетрудно
также проверить, что точка y
производит золотое сечение отрезка
![]() ,
а точка z
производит золотое сечение отрезка
,
а точка z
производит золотое сечение отрезка
![]() .
На этом свойстве, позволяющем на каждой
итерации вычислить значение функции
лишь в одной пробной точке, и основан
алгоритм золотого сечения.
.
На этом свойстве, позволяющем на каждой
итерации вычислить значение функции
лишь в одной пробной точке, и основан
алгоритм золотого сечения.
Алгоритм метода золотого сечения.
Рассмотрим задачу
Исходные данные – отрезок, содержащий точку максимума, - параметр окончания счета.
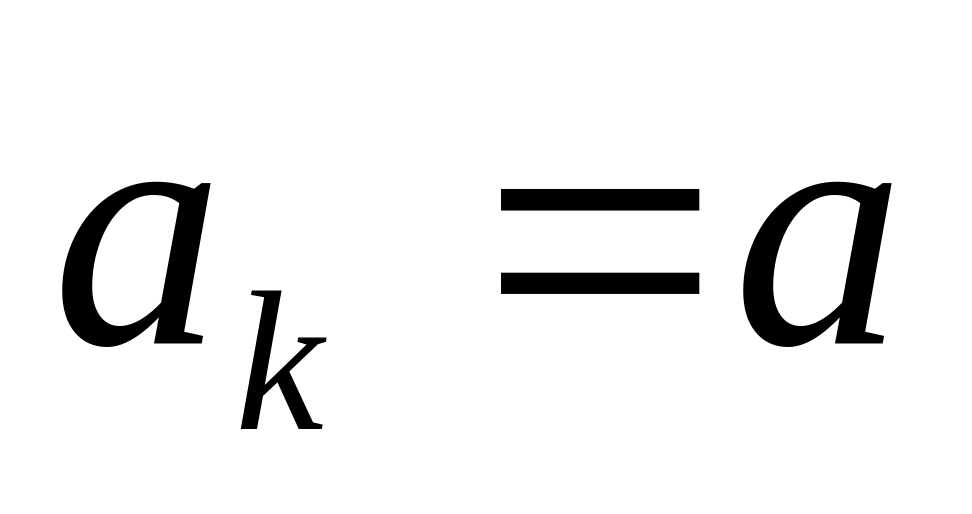 ,
,
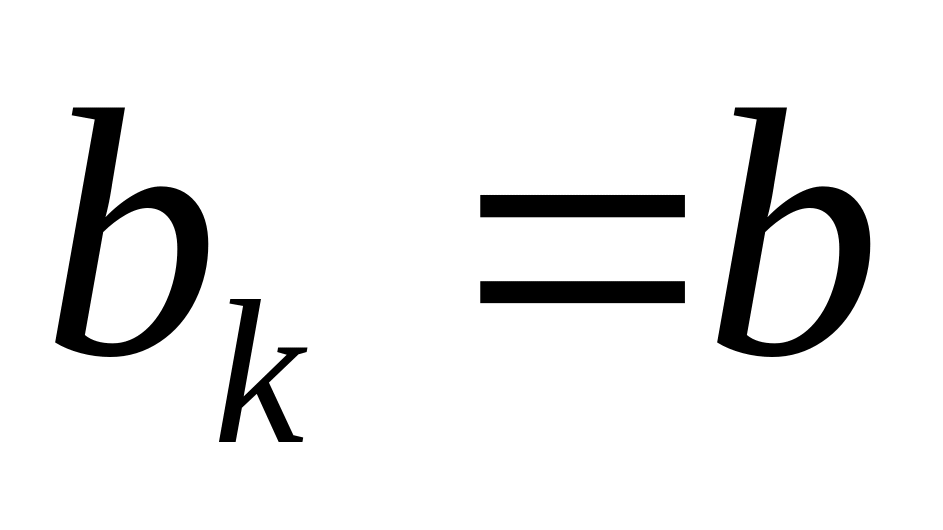 ,
,
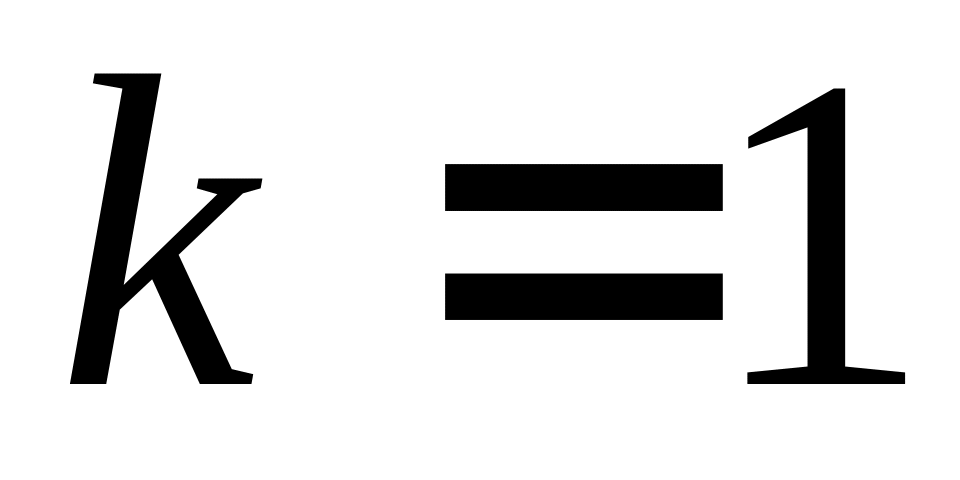 .
.
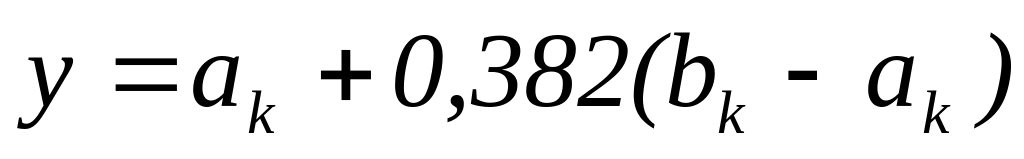 ;
;
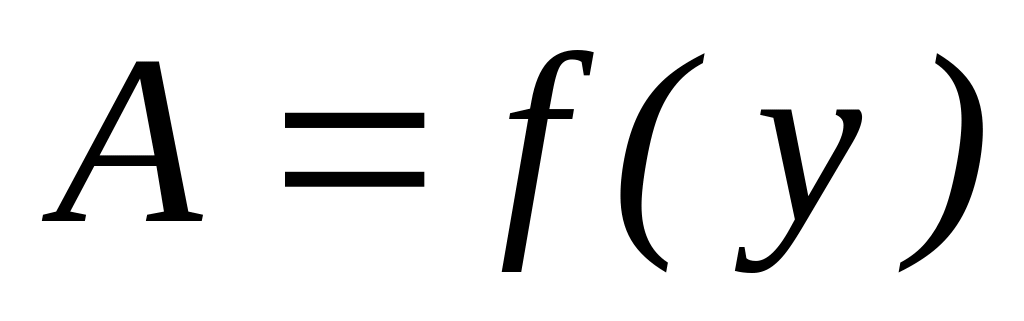 ;
;
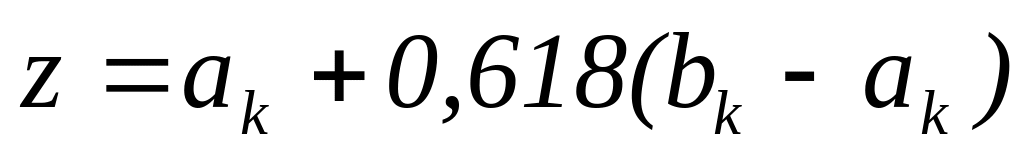 ;
;
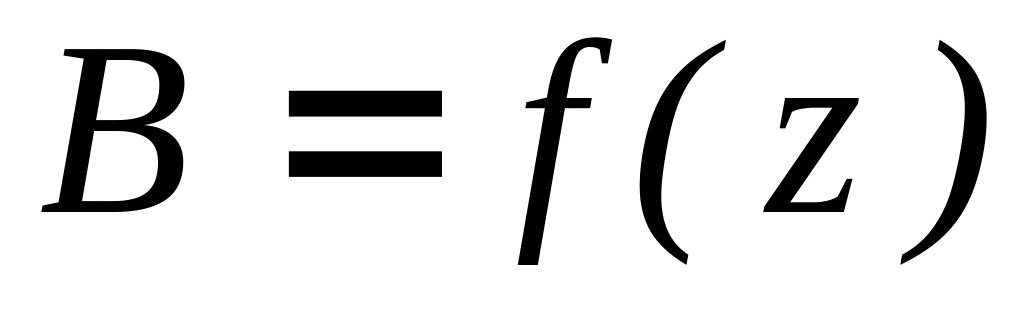 .
.Если , то перейти к шагу 4.
, ;
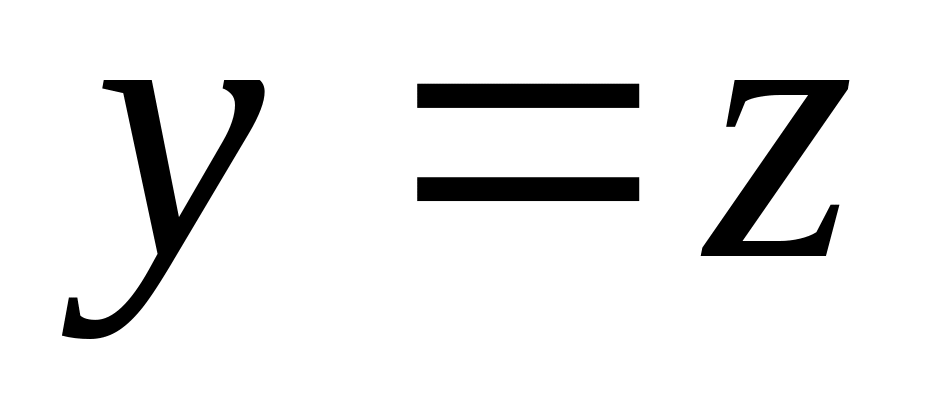 ;
;
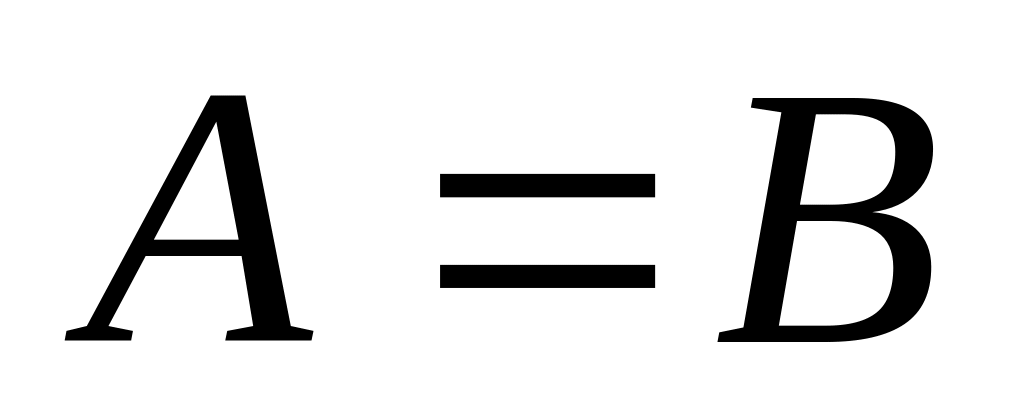 .
.
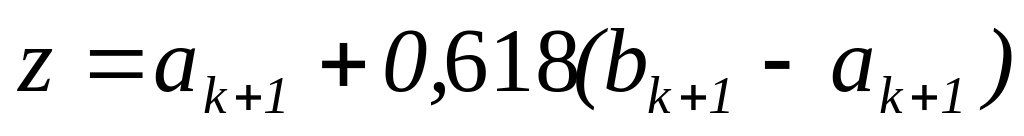 ;
,
перейти к шагу 5.
;
,
перейти к шагу 5., ;
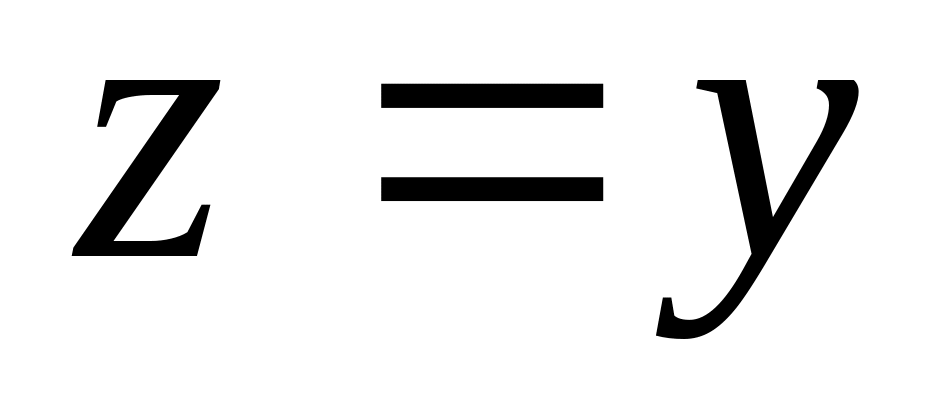 ;
;
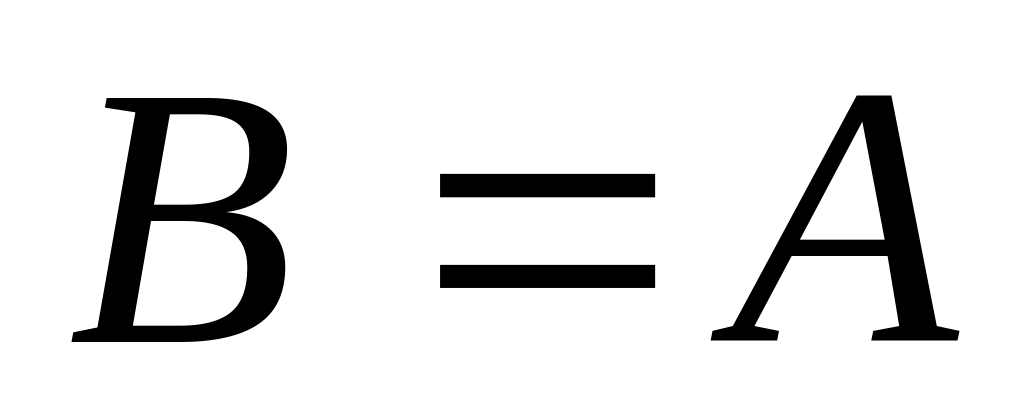 ;
;
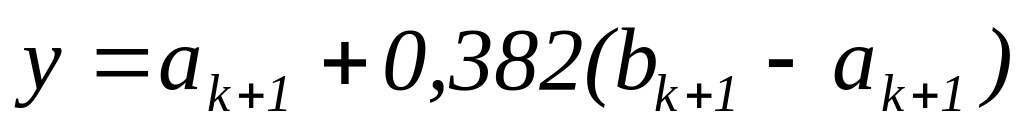 ;
;
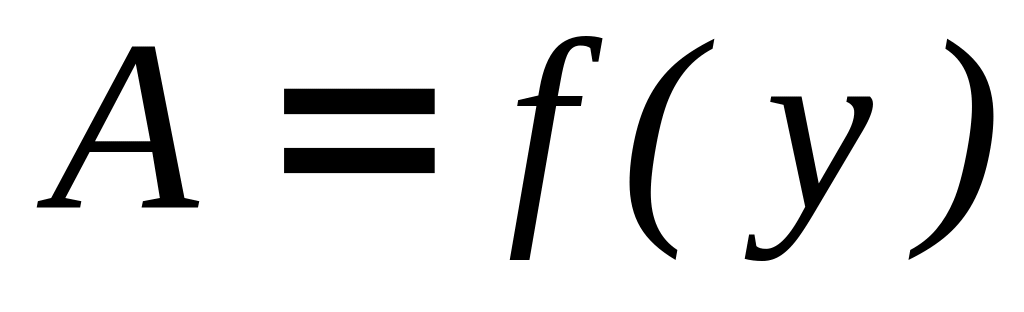 .
.Если
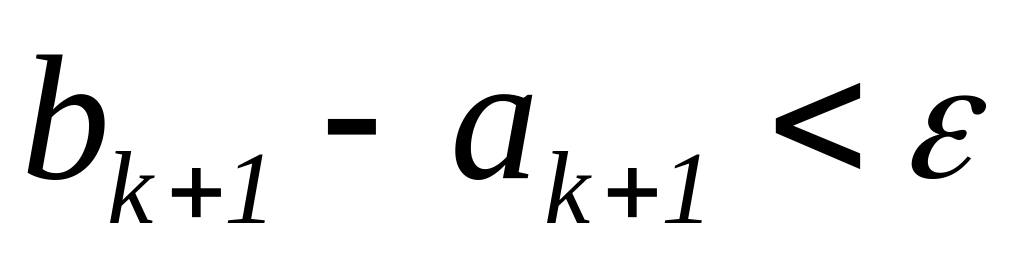 ,
то
,
то
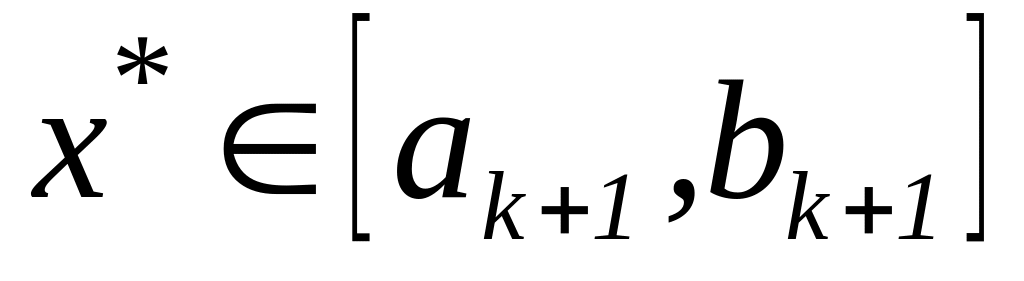 ,
конец.
,
конец., перейти к шагу 2.
Пример
7.3.
Найти точку максимума функции
![]() на отрезке
;
на отрезке
;
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ;
;
![]() .
.
Итерация 1
Так
как
,
то
![]() ,
;
,
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Итерация 2
Так
как
,
то
![]() ,
;
,
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Итерация 3.
Так
как
,
то
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Итерация 4
Так
как
,
то
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
следовательно,
,
следовательно,
![]() .
.
Как
было отмечено выше, на каждой итерации
метода золотого сечения производится
лишь одно вычисление значения функции.
При этом длина полученного в результате
одной итерации отрезка составляет
![]() ,
где
,
где
![]() -
длина исходного интервала.
-
длина исходного интервала.
Если сравнить методы дихотомического поиска и золотого сечения, используя в качестве критерия эффективности относительное уменьшение исходного интервала F, то

т.е. метод золотого сечения оказывается более эффективным [4].
