- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
Первый вариант
Начальный
этап. Задать начальную точку
,
– параметр окончания счета,
![]() – первоначальная величина шага,
– первоначальная величина шага,
![]() – коэффициент уменьшения шага, положить
– коэффициент уменьшения шага, положить
![]() ,
,
![]() .
.
Основной этап.
Вычислить
 .
.Если
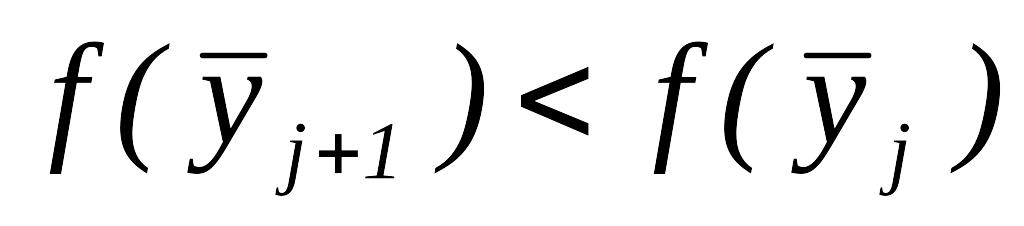 ,
то перейти к шагу 5.
,
то перейти к шагу 5.Вычислить
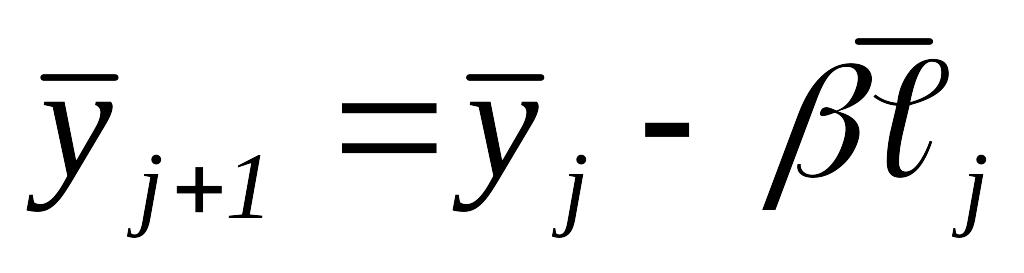 .
.Если , то перейти к шагу 5, иначе положить
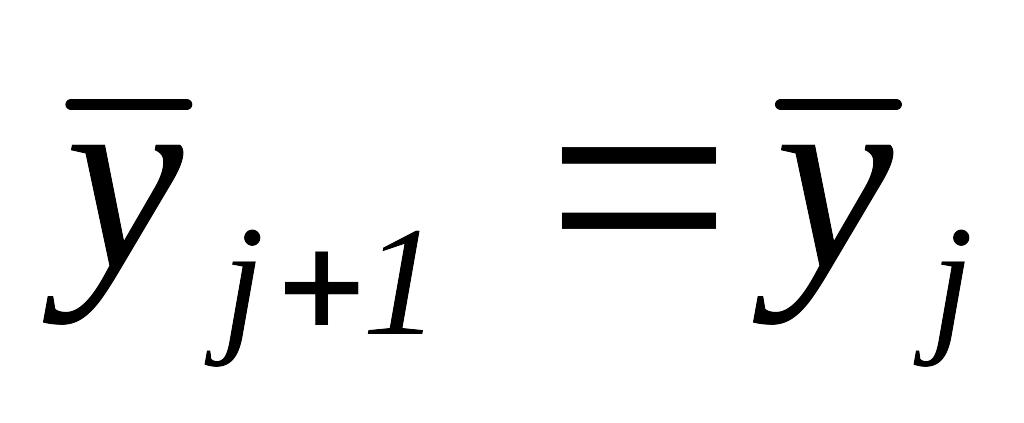 .
.Если
 ,
то положить
и перейти к шагу 1.
,
то положить
и перейти к шагу 1.Положить
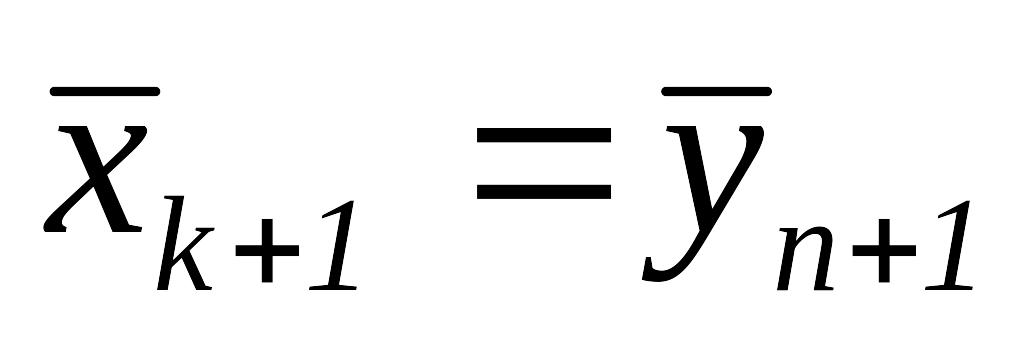 .
.Если
 ,
то перейти к шагу 9, иначе перейти к шагу
8.
,
то перейти к шагу 9, иначе перейти к шагу
8.Если
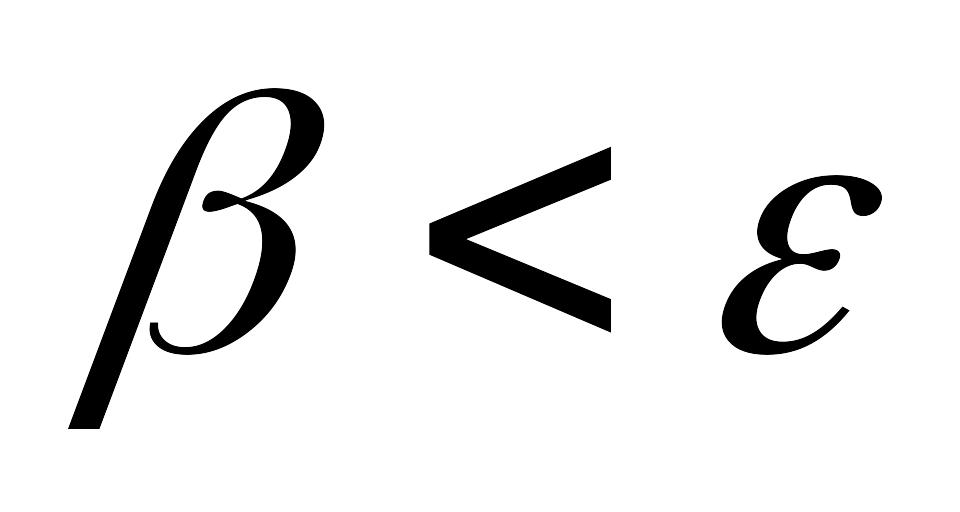 ,
то положить
,
то положить
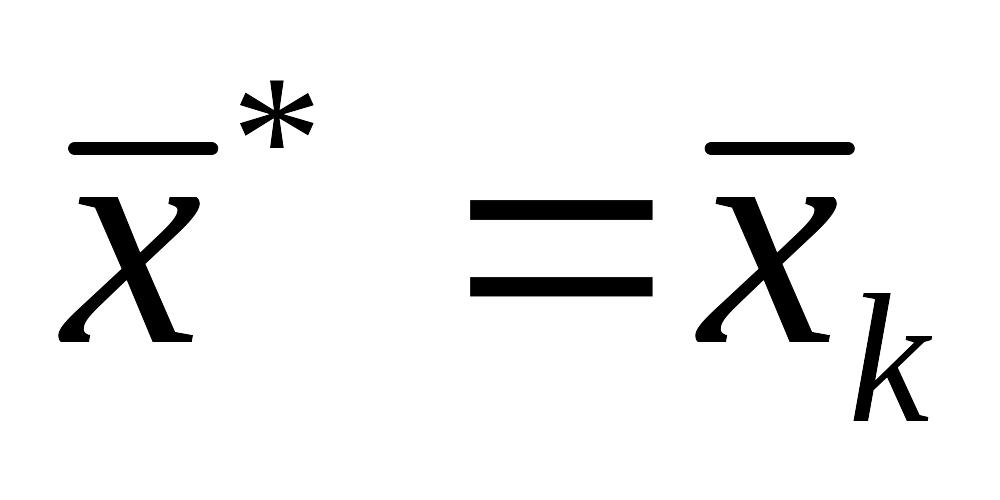 и остановиться, иначе положить
и остановиться, иначе положить
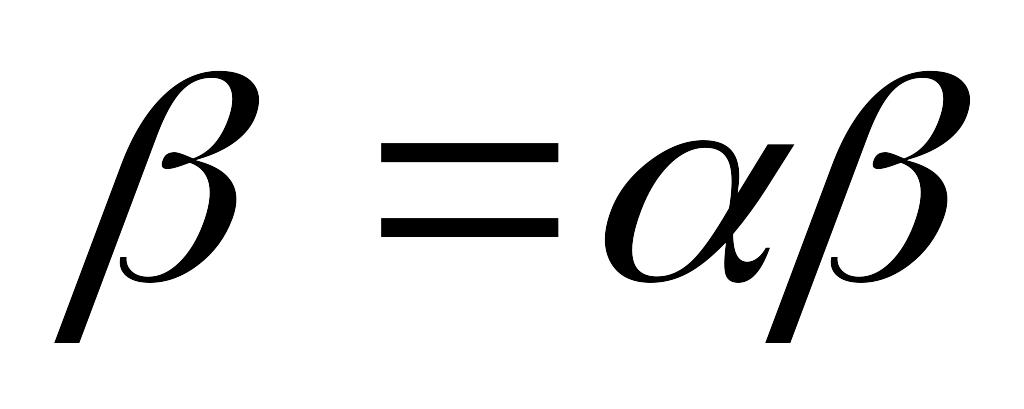 ,
,
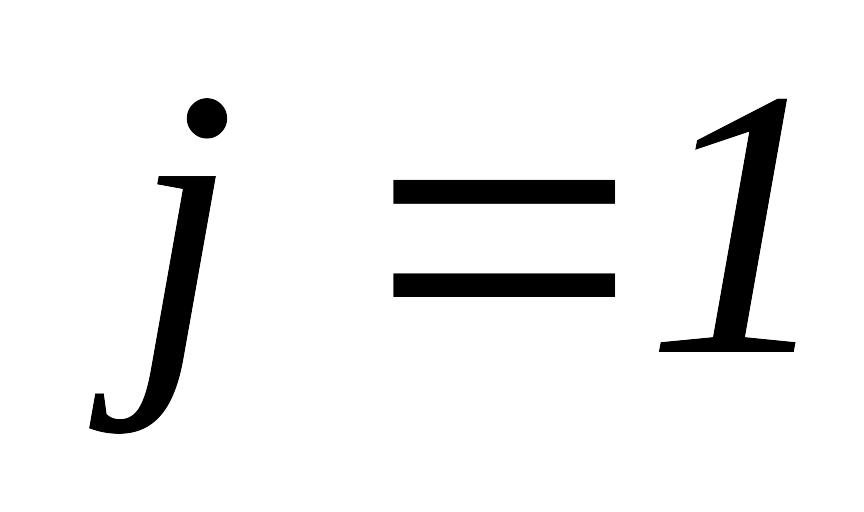 ,
,
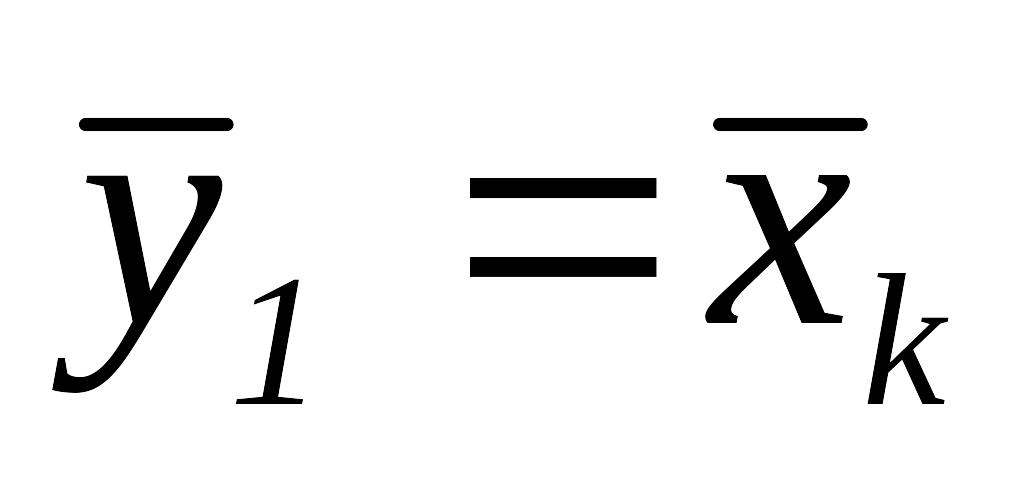 и перейти к шагу 1.
и перейти к шагу 1.Если
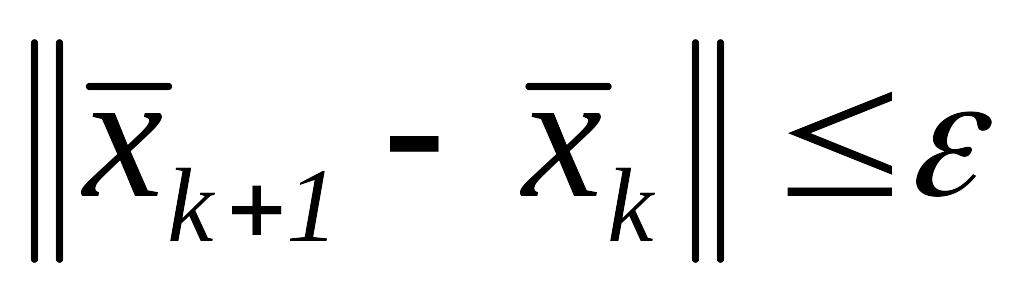 ,
то положить
,
то положить
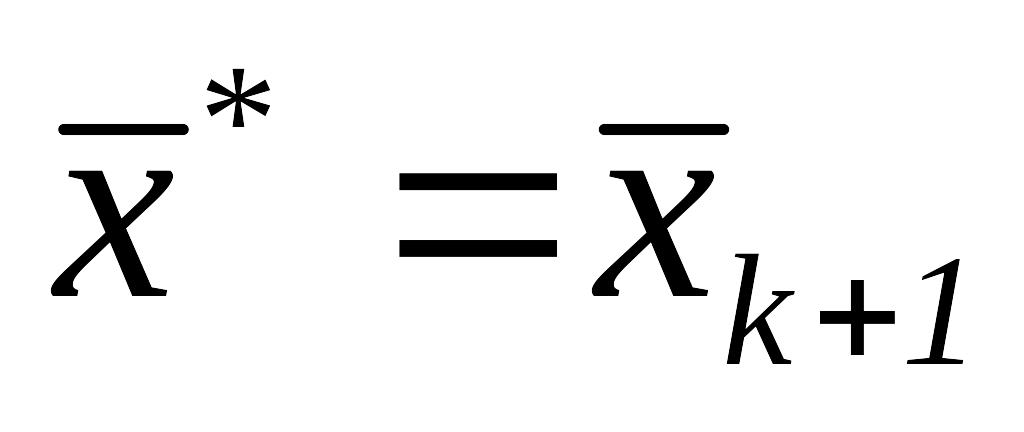 и остановиться, иначе положить
и остановиться, иначе положить
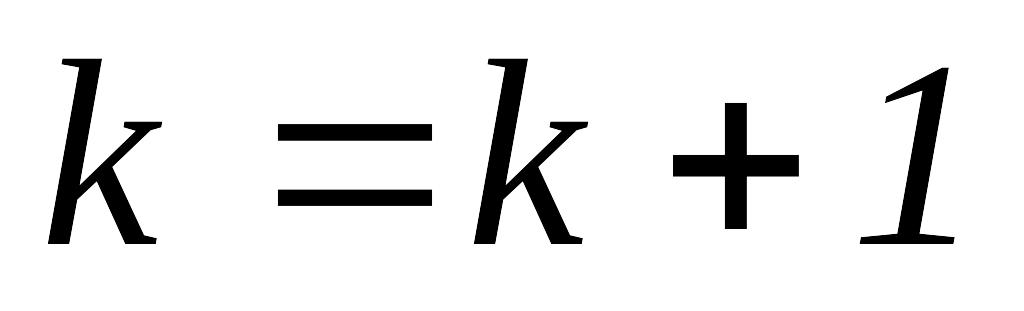 ,
,
,
,
 и перейти к шагу 1.
и перейти к шагу 1.
Второй вариант
Начальный этап. Такой же, как в первом варианте.
Основной этап.
Вычислить .
Если , то перейти к шагу 6.
Вычислить .
Если , то перейти к шагу 6.
Если , то перейти к шагу 6, иначе положить и перейти к шагу 1.
Если
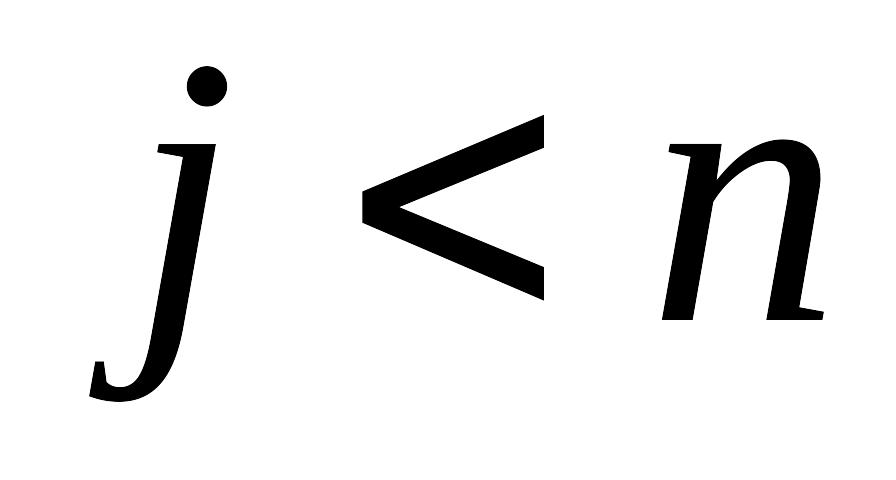 ,
то положить
и перейти к шагу 1.
,
то положить
и перейти к шагу 1.Положить .
Если , то положить и остановиться, иначе положить , , и перейти к шагу 1.
Если
пользоваться терминологией Хука-Дживса,
то метод покоординатного спуска, не
использующий одномерной оптимизации,
состоит из последовательности ИП вокруг
текущей (базисной) точки и не предполагает
поиска по образцу, что во многих случаях
замедляет сходимость. ИП вокруг текущей
точки
состоит из n-итераций,
каждая из которых состоит из поиска
точки на соответствующей координатной
оси
![]() .
Величина шага
вдоль оси определяется так называемым
методом удвоения (название метода
соответствует случаю, когда
.
Величина шага
вдоль оси определяется так называемым
методом удвоения (название метода
соответствует случаю, когда
![]() ;
;
![]() ).
В первом варианте алгоритма величина
шага
вдоль оси остается постоянной при
проведении ИП вокруг текущей точки
и уменьшается лишь тогда, когда ИП не
приводит к уменьшению значения функции
).
В первом варианте алгоритма величина
шага
вдоль оси остается постоянной при
проведении ИП вокруг текущей точки
и уменьшается лишь тогда, когда ИП не
приводит к уменьшению значения функции
![]() .
Во втором варианте алгоритма величина
шага
может меняться при поиске вдоль каждой
из координатных осей, причем как в
сторону уменьшения шага (
),
если значение функции не уменьшилось,
так и в сторону увеличения шага (
),
если значение функции уменьшилось,
причем процесс увеличения
продолжается до тех пор, пока убывание
функции не прекратится.
.
Во втором варианте алгоритма величина
шага
может меняться при поиске вдоль каждой
из координатных осей, причем как в
сторону уменьшения шага (
),
если значение функции не уменьшилось,
так и в сторону увеличения шага (
),
если значение функции уменьшилось,
причем процесс увеличения
продолжается до тех пор, пока убывание
функции не прекратится.
Пример 12.4. Решить задачу из примера 12.1 методом покоординатного спуска (второй вариант).
Начальный
этап. Положить
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() .
.
Основной этап.
Вычислить
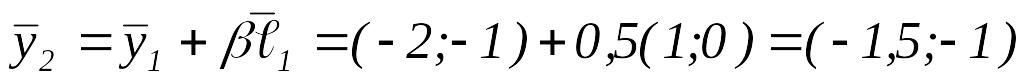 .
.Так как
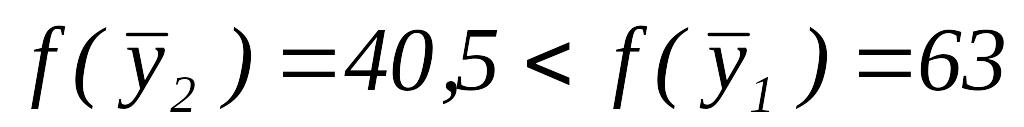 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как
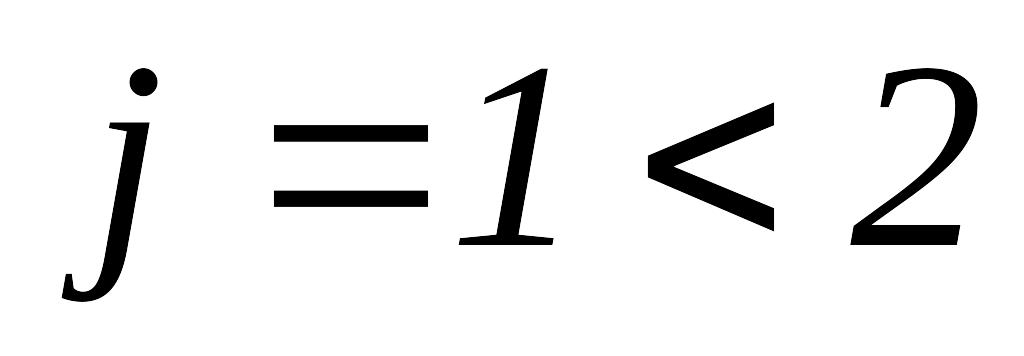 ,
то
,
то
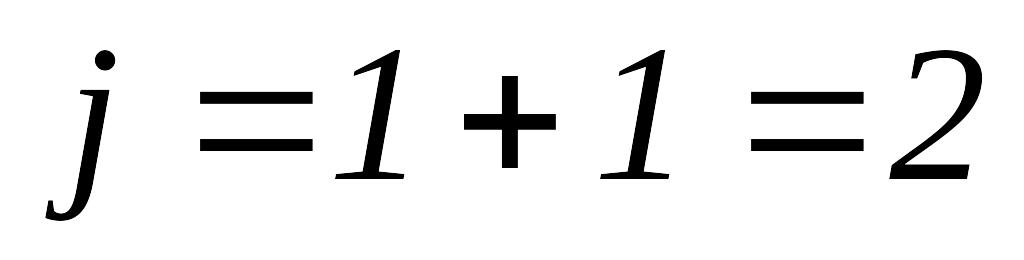 и переходим к шагу 1
и переходим к шагу 1
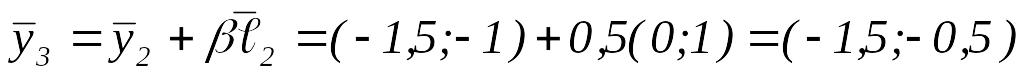 .
.Так как
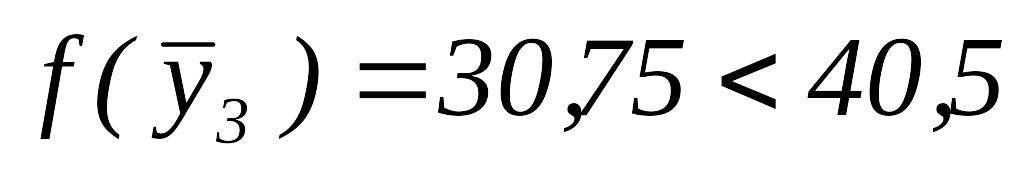 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как
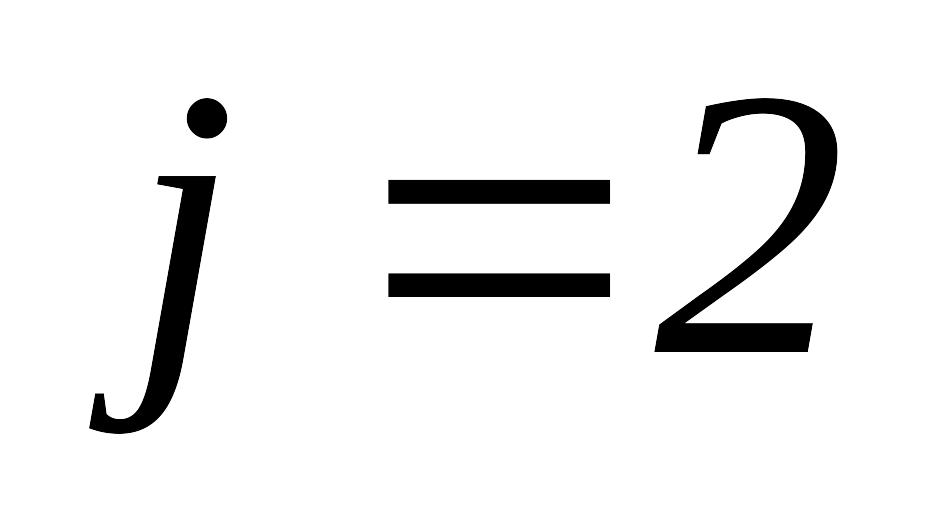 ,
то переходим к шагу 7.
,
то переходим к шагу 7.Вычислим
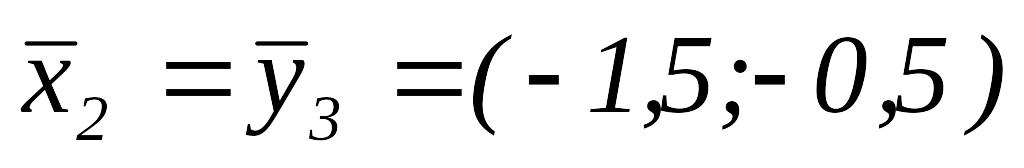 .
.Так как
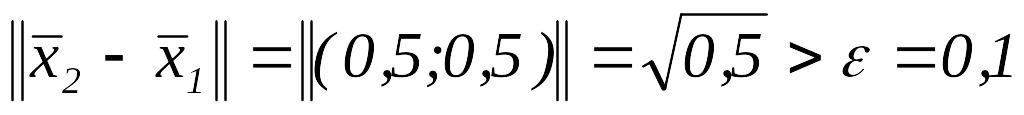 ,
то полагаем
,
то полагаем
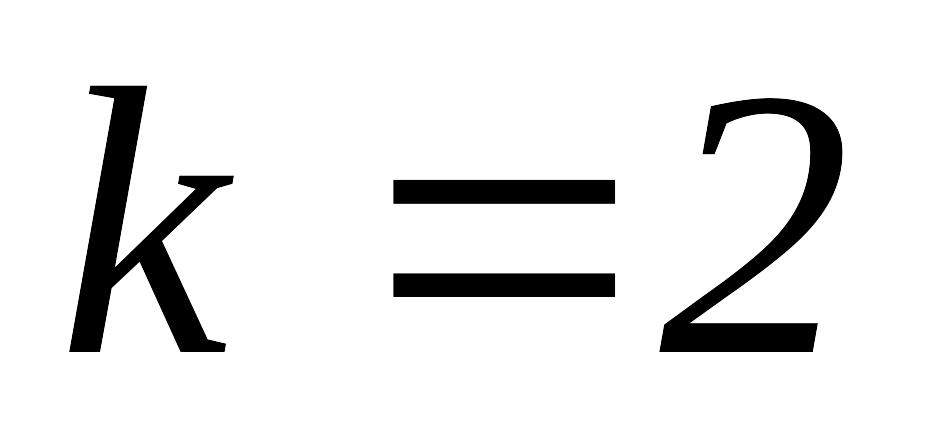 ,
,
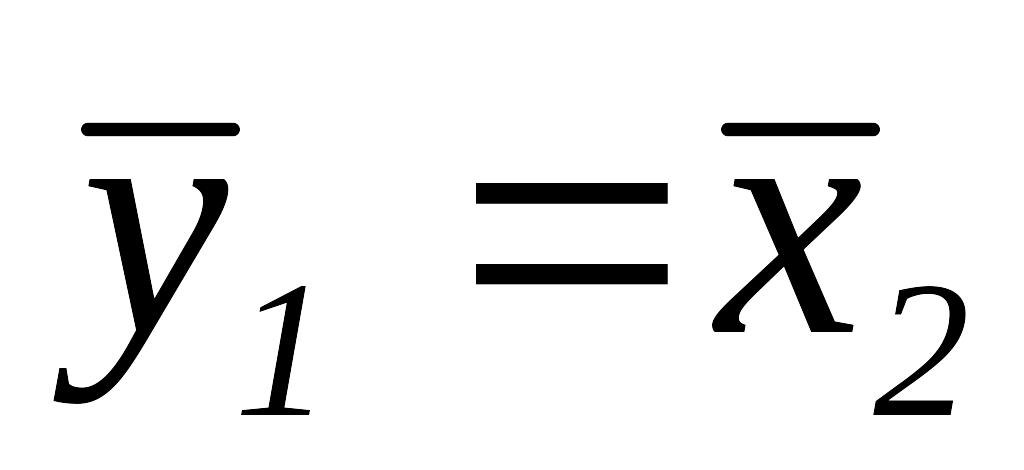 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
 .
.Так как
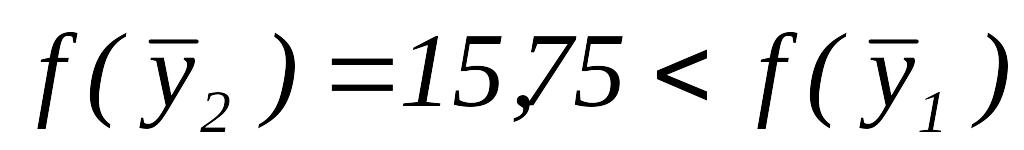 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как , то и переходим к шагу 1
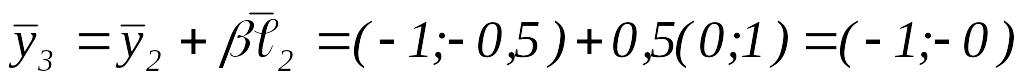 .
.Так как
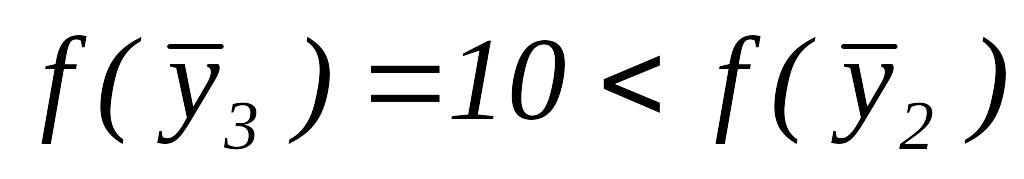 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как , то переходим к шагу 7.
Положим
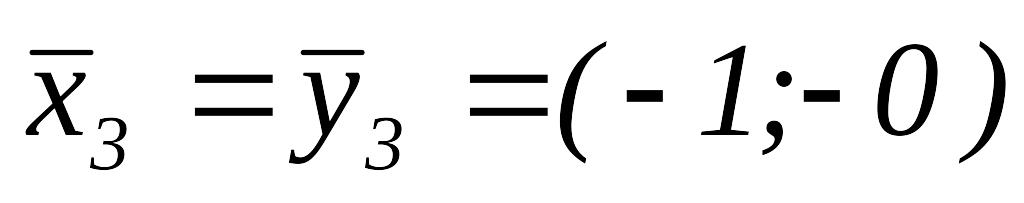 .
.Так как
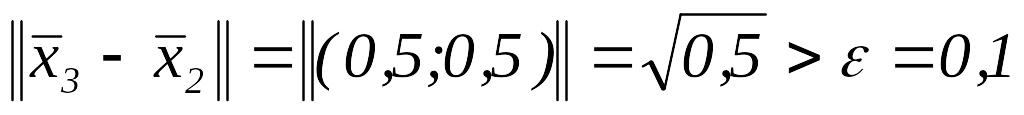 ,
то полагаем
,
то полагаем
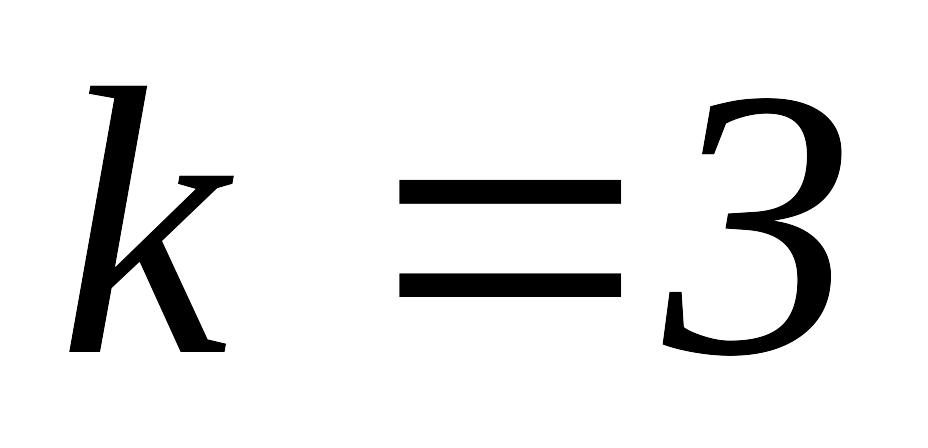 ,
,
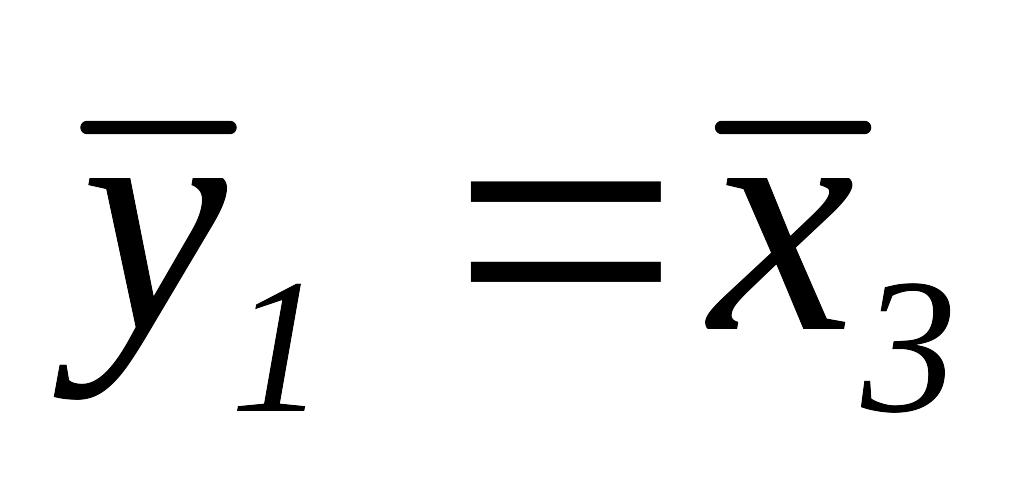 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
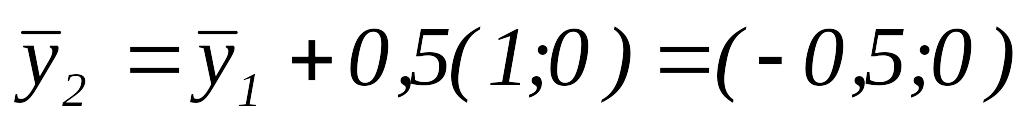 .
.Так как
 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как , то и переходим к шагу 1
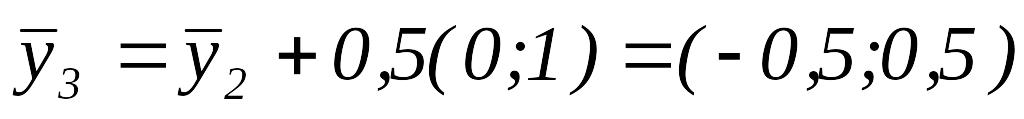 .
.Так как
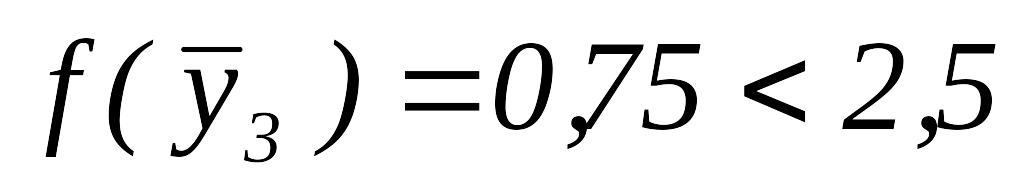 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как , то переходим к шагу 7.
Положим
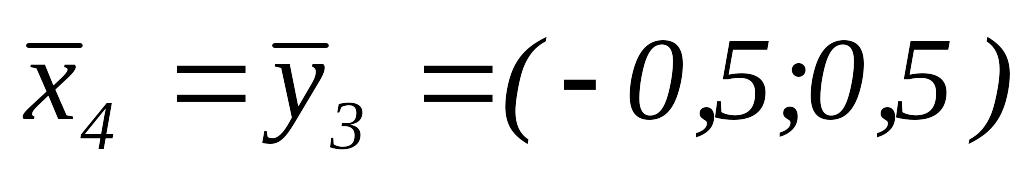 .
.Так как
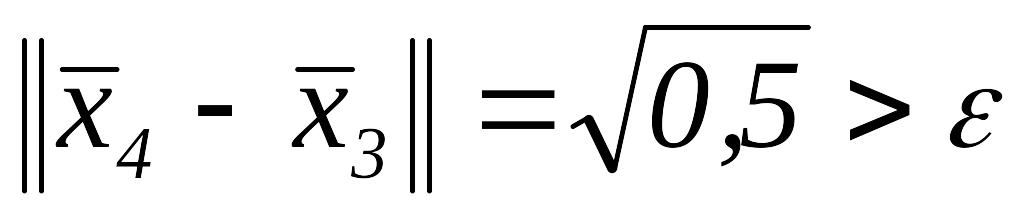 ,
то полагаем
,
то полагаем
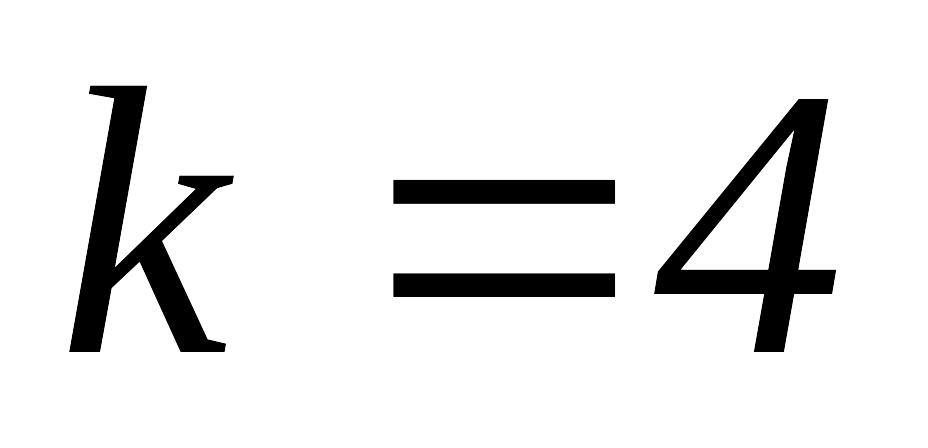 ,
,
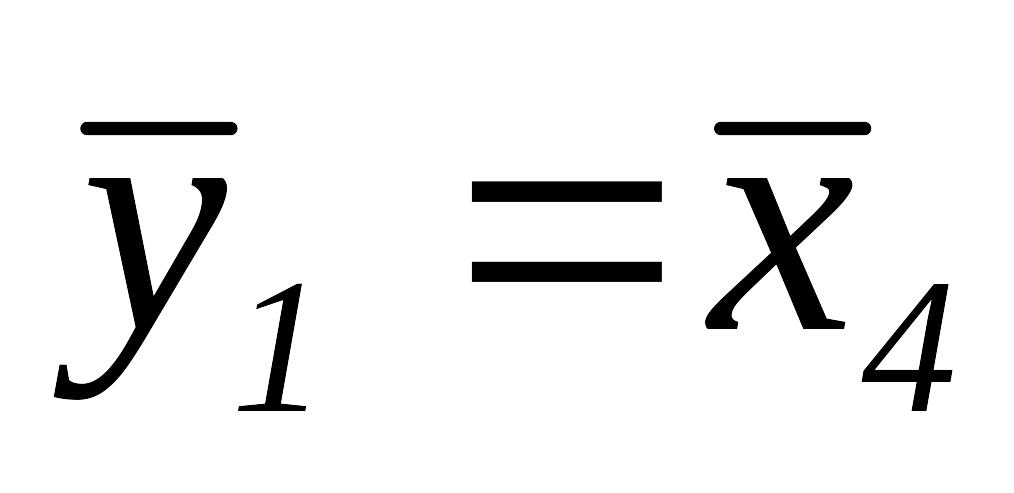 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
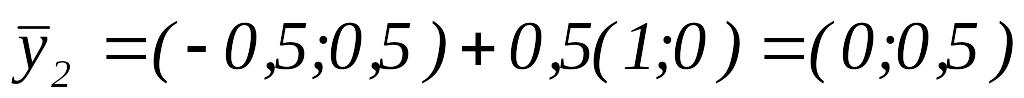 .
.Так как
 ,
то переходим к шагу 3.
,
то переходим к шагу 3.Вычислим
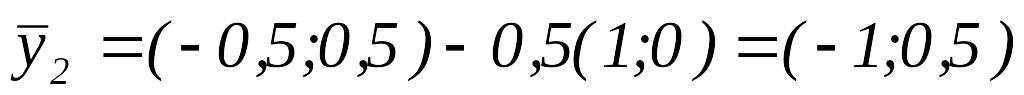 .
.Так как
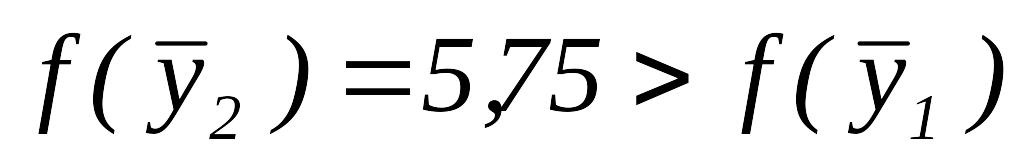 ,
то переходим к шагу 5.
,
то переходим к шагу 5.Так как
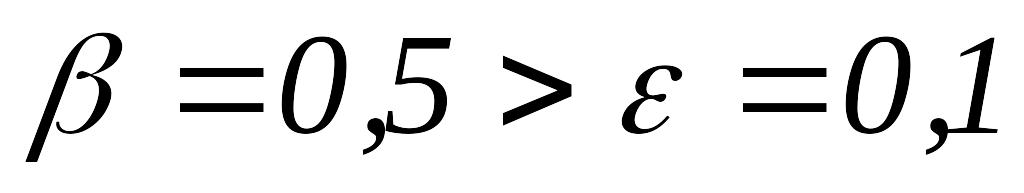 ,
полагаем
,
полагаем
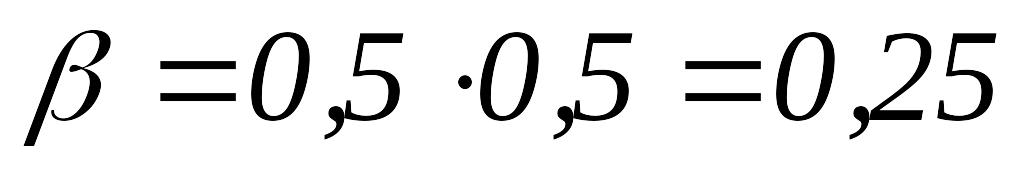 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
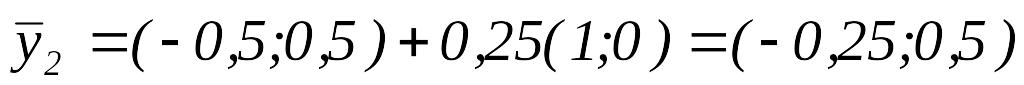 .
.Так как
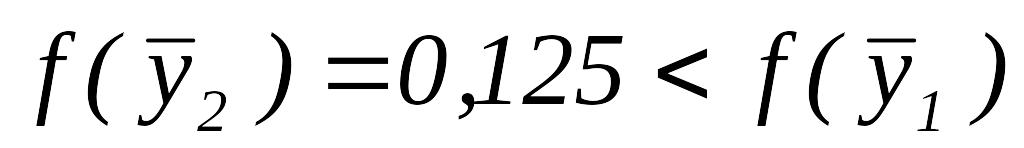 ,
то переходим к шагу 6.
,
то переходим к шагу 6.
Так как , то переходим к шагу 1
Вычислить
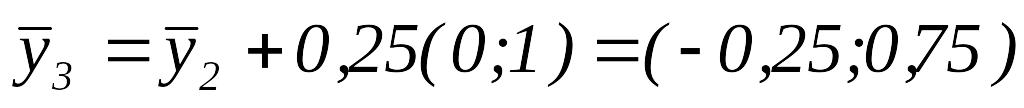 .
.Так как
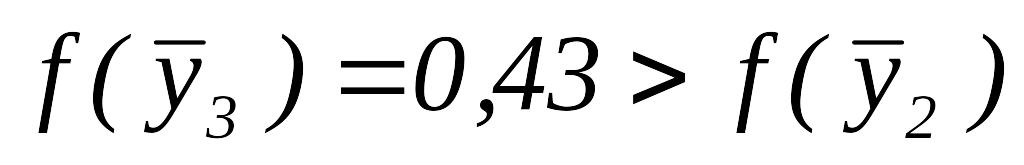 ,
то переходим к шагу 3.
,
то переходим к шагу 3.Вычислим
 .
.Так как
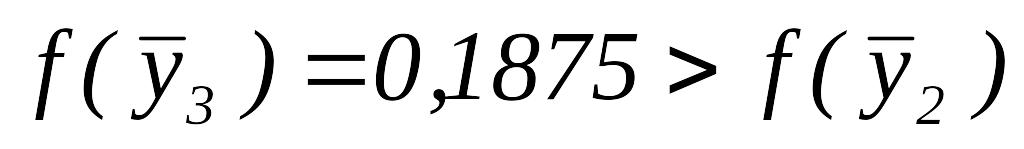 ,
то переходим к шагу 5.
,
то переходим к шагу 5.Так как
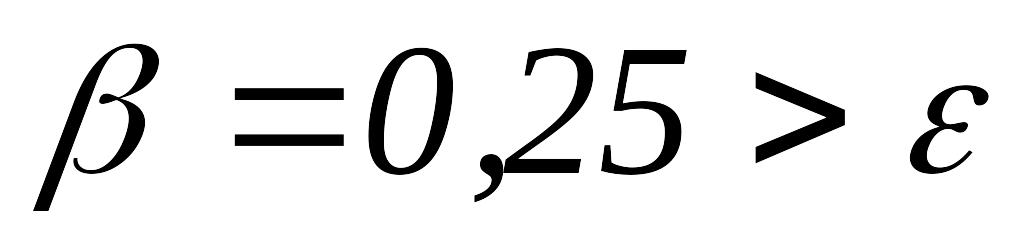 ,
полагаем
,
полагаем
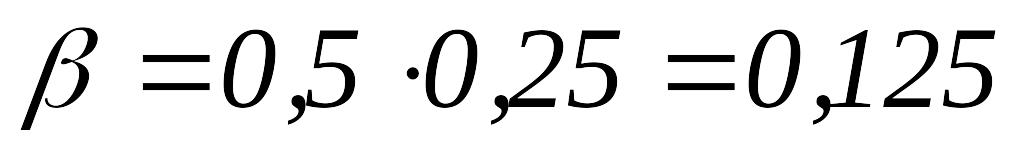 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
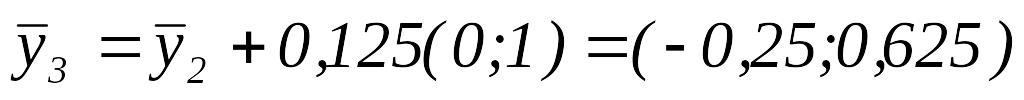 .
.Так как
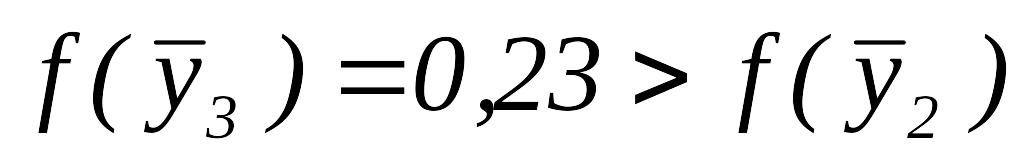 ,
то переходим к шагу 3.
,
то переходим к шагу 3.Вычислим
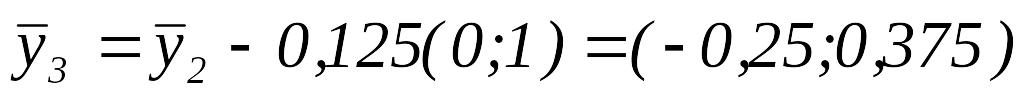 .
.Так как
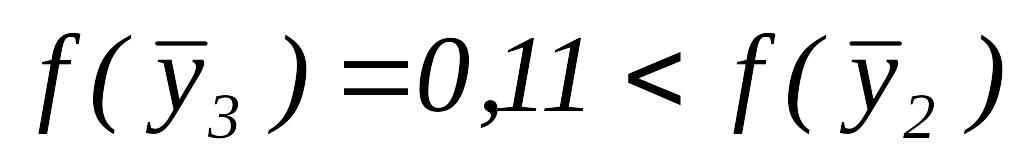 ,
то переходим к шагу 7.
,
то переходим к шагу 7.
Положим
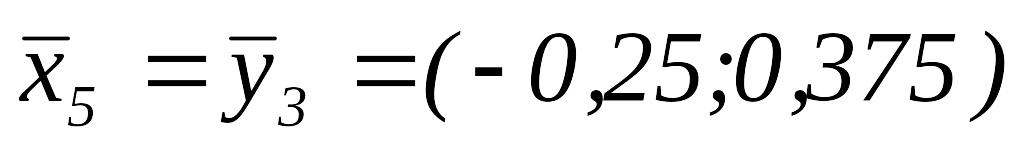 .
.Так как
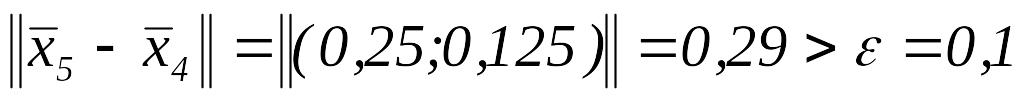 ,
то полагаем
,
то полагаем
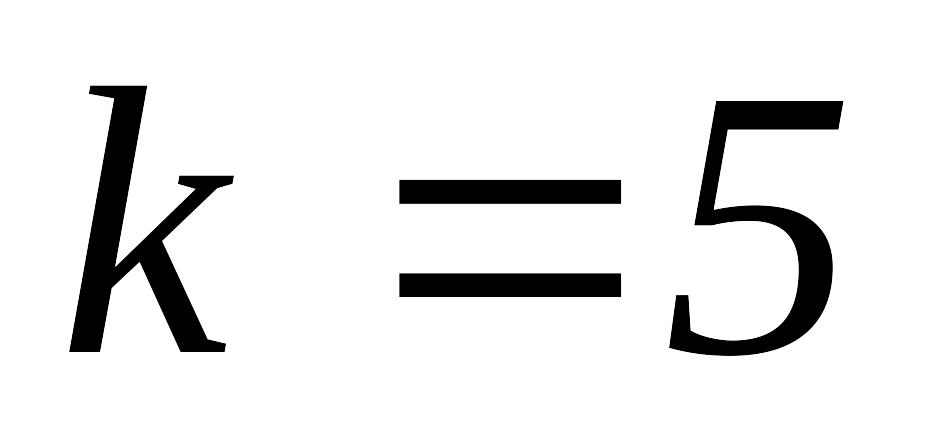 ,
,
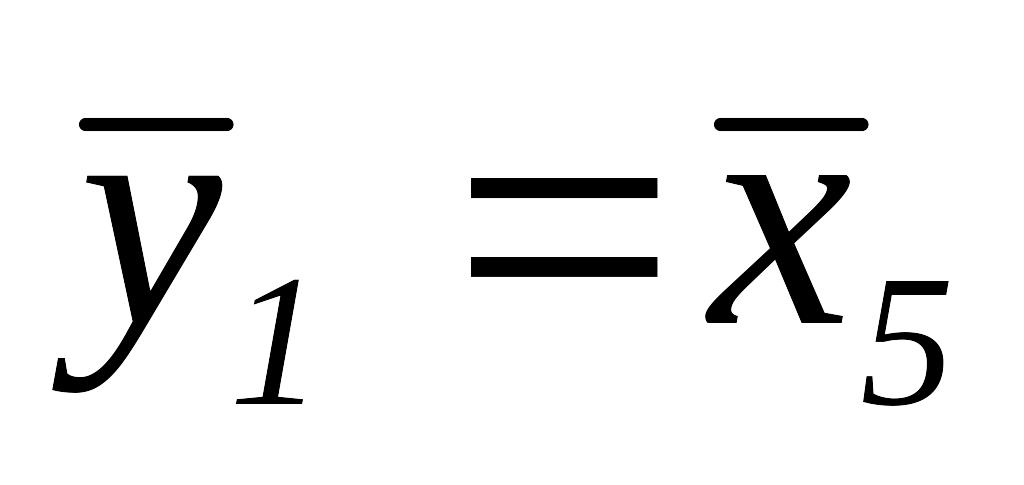 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
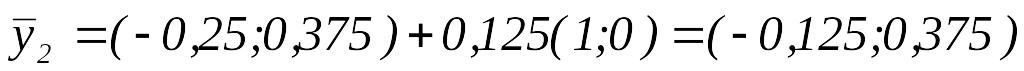 .
.Так как
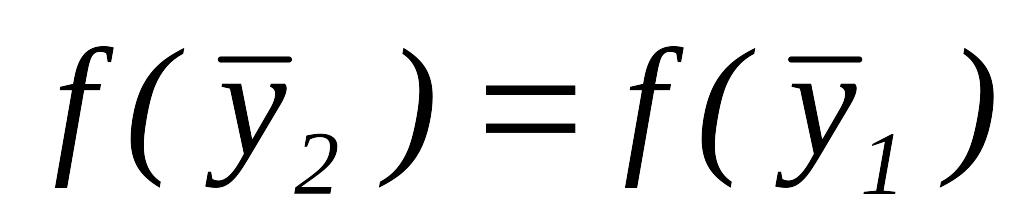 ,
то переходим к шагу 3.
,
то переходим к шагу 3.Вычислим
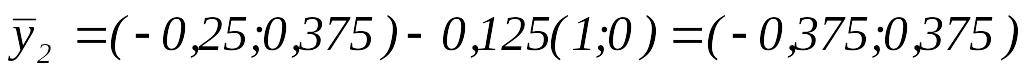 .
.Так как
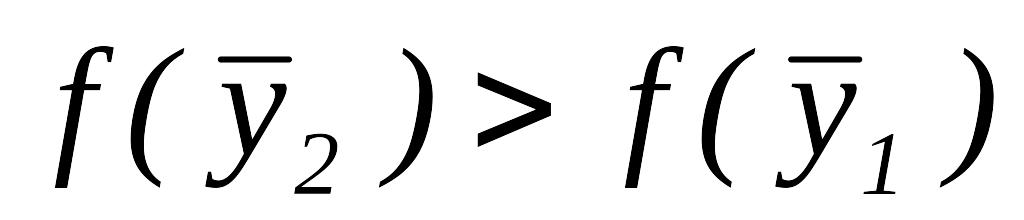 ,
то переходим к шагу 5.
,
то переходим к шагу 5.Так как
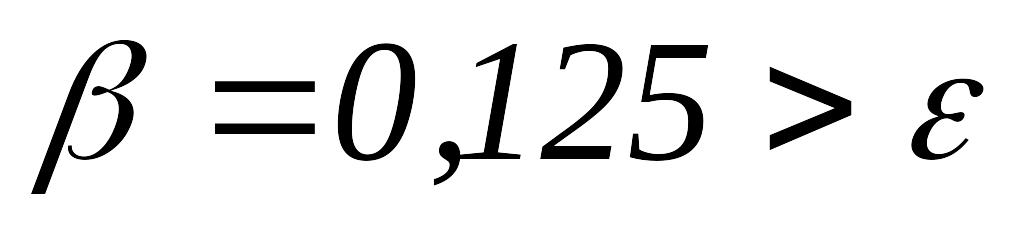 ,
полагаем
,
полагаем
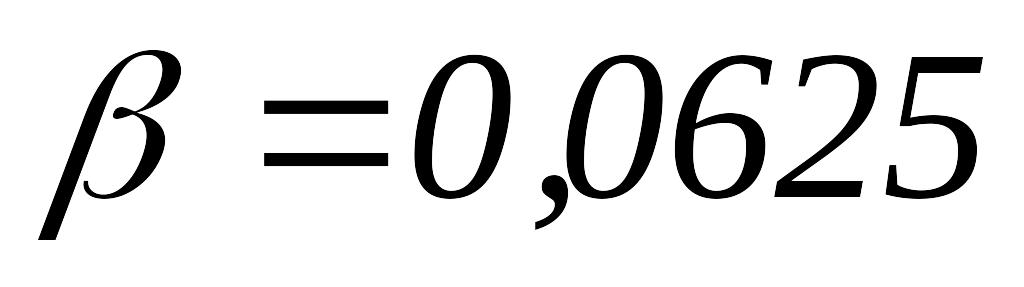 и переходим к шагу 1.
и переходим к шагу 1.
Вычислить
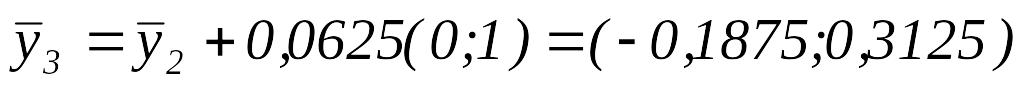 .
.Так как
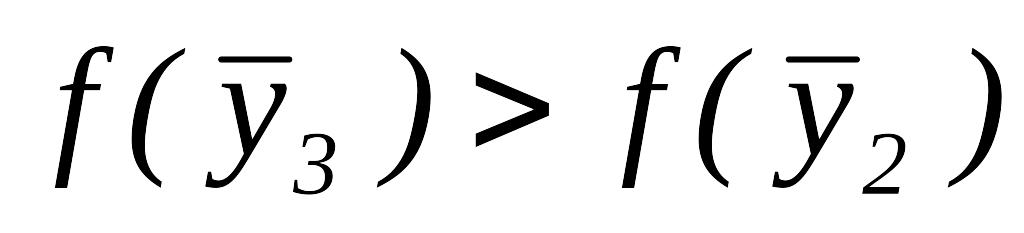 ,
то переходим к шагу 3.
,
то переходим к шагу 3.Вычислим
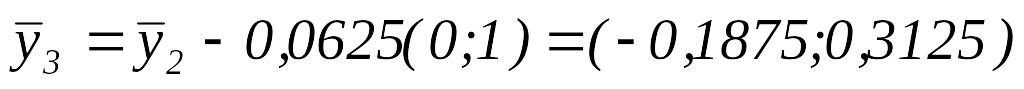 .
.Так как
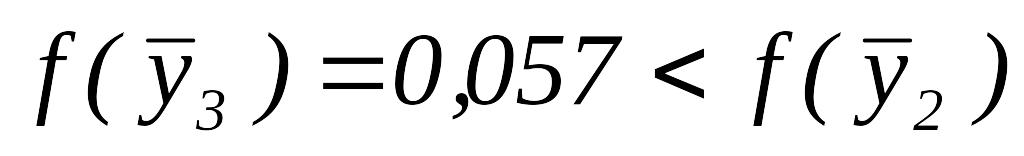 ,
то переходим к шагу 7.
,
то переходим к шагу 7.
Положим
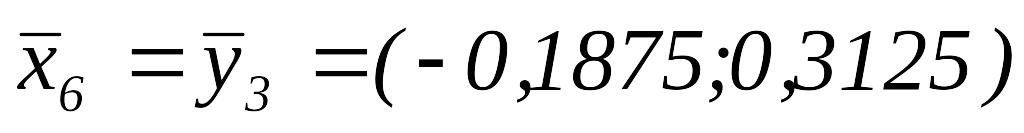 .
.Так как
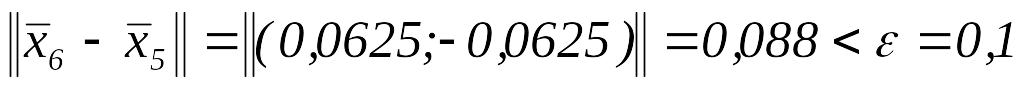 ,
то положим
,
то положим
 ,
,
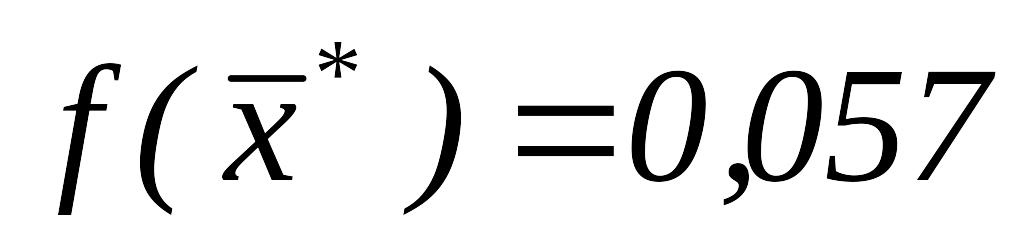 и остановимся.
и остановимся.
Итак,
после пяти итераций получена точка
![]() .
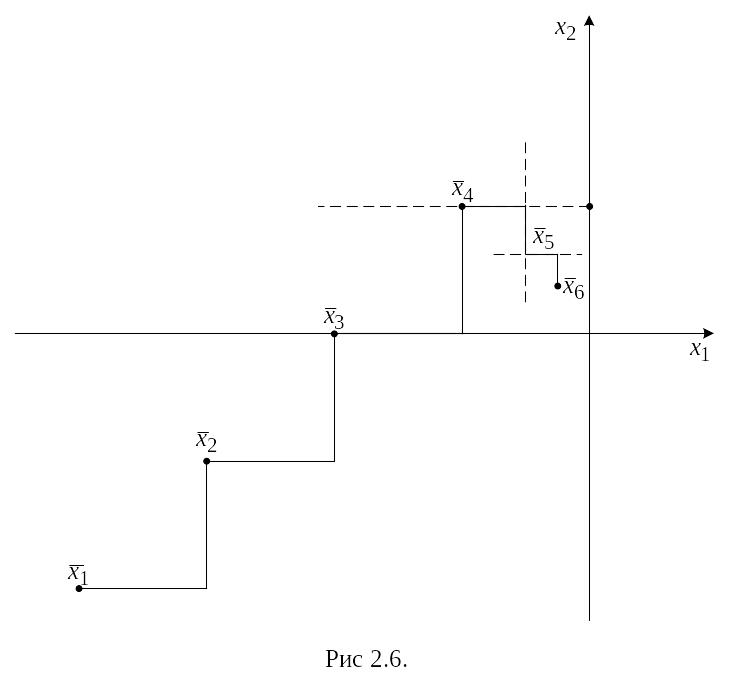
На рис. 12.6 представлены соответствующие
шаги алгоритма. Пунктирная линия
соответствует неудачным шагам поиска.
.
На рис. 12.6 представлены соответствующие
шаги алгоритма. Пунктирная линия
соответствует неудачным шагам поиска.