
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
13.2.3. Метод Франка-Вульфа
Пусть решается следующая задача:
(13.20)
при условиях
![]() ,
,
,
,
![]() ,
,
![]() .
(13.21)
.
(13.21)
Отметим, что система ограничений этой задачи содержит только линейные неравенства. Это является основой для замены в окрестности исследуемой точки нелинейной целевой функции линейной, благодаря чему решения исходной задачи сводится к последовательному решению задач линейного программирования.
Алгоритм метода Франка-Вульфа
Начальный этап. Выбрать , , .
Основной этап.
Шаг 1. Определить .
Шаг 2. Решается задача:
![]() (13.22)
(13.22)
![]() -
решение этой задачи.
-
решение этой задачи.
Шаг
3. Если
![]() ,
то
-
задача решена.
,
то
-
задача решена.
Шаг
4. Выбираем направление
![]() .
.
Шаг 5. Находим (величина шага в направлении ), решая задачу одномерной оптимизации: .
Шаг
6. Положить
.
Определить
![]() .
.
Шаг
7. Если
![]() ,
то задача решена, в противном случае
положить
и перейти к шагу 1.
,
то задача решена, в противном случае
положить
и перейти к шагу 1.
Очевидно, что эту процедуру можно интерпретировать как метод возможных направлений. В самом деле, алгоритм Франка-Вульфа предусматривает, что исследуемые точки не выходят за пределы области допустимых решений задачи, а направление является возможным на каждой итерации метода.
Пример 13.5. Найти максимум функции
![]() (13.23)
(13.23)
при условиях
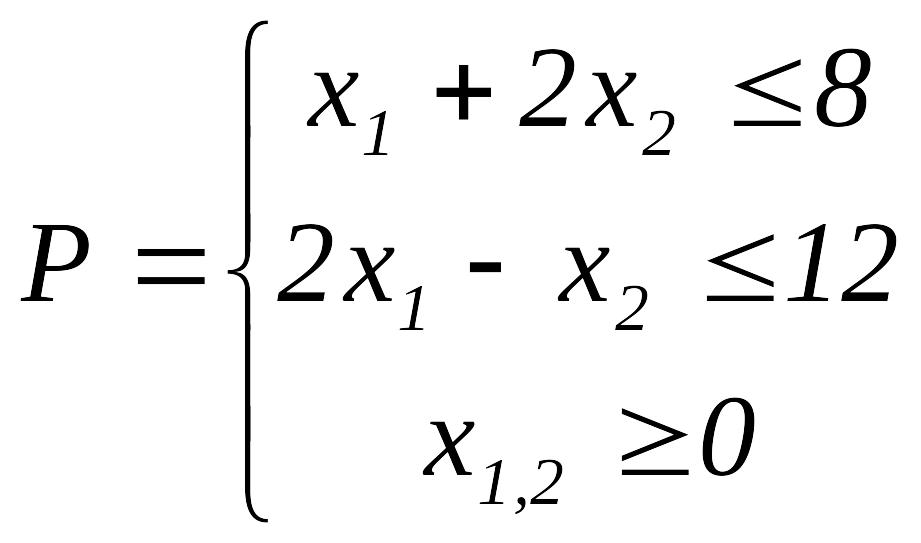 .
(13.24)
.
(13.24)
Начальный
этап. Выбираем
начальную точку
![]() ,
,
,
,
![]() ,
.
,
.
Основной этап.
Итерация 1
Шаг
1. Определяем
![]() .
.
Шаг 2. Решаем задачу:
![]() ,
,
![]() ;
фактически решаем задачу
;
фактически решаем задачу
![]() .
.
Оптимальный
план этой задачи
![]() .
.
Шаг
3. Так как
![]() ,
переходим к шагу 4.
,
переходим к шагу 4.
Шаг
4. Выбираем
![]() .
.
Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
Шаг 6. Находим новую точку:
![]() .
.
![]() .
.
Шаг
7. Так как
![]() ,
то
и перейти к шагу 1.
,
то
и перейти к шагу 1.
Итерация 2
Шаг
1. ![]() .
.
Шаг
2. Решаем вспомогательную задачу:
![]() .
Решением является
.
Решением является
![]() .
.
Шаг 3. Так как , переходим к шагу 4.
Шаг
4. Выбираем
![]() .
.
Шаг 5. Решаем задачу: .
Шаг
6. Положить
![]() .
.
![]() .
.
Шаг
7. Так как
![]() ,
то
и перейти к шагу 1.
,
то
и перейти к шагу 1.
Итерация 3
Шаг
1. ![]() .
.
Шаг
2. Решаем вспомогательную задачу:
![]() .
Решением является
.
Решением является
![]() .
.
Шаг
3. Так как
![]() ,
переходим к шагу 4.
,
переходим к шагу 4.
Шаг
4. Выбираем
![]() .
.
Шаг
5. Решаем задачу:
![]() .
.
![]() .
.
Решение
задачи
![]() .
.
Шаг
6. Положить
![]() .
.
![]() .
.
Шаг
7. Так как
![]() ,
то
,
то
![]() и задача решена.
и задача решена.
Замечание.
Задав меньшее значение
,
можно было, выполнив дополнительные
итерации, ещё ближе подойти к точке
максимального значения целевой функции
(очевидно, что это точка
![]() ).
).
Ход решения задачи проиллюстрирован на рис. 13.9.
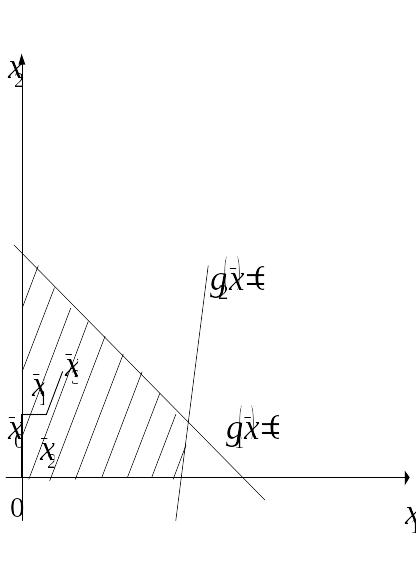
Рисунок 13.9. Метод Франка-Вульфа
Рассмотренные методы возможных направлений имеют две особенности – гарантированная сходимость для невыпуклых задач и допустимость получаемых точек. В качестве основных недостатков следует отметить медленную сходимость и неспособность удовлетворительно решать задачи с нелинейными ограничениями в виде равенств, так как у таких ограничений отсутствует допустимая внутренняя область.
В задаче выбора направлений берутся направления градиентного подъема. Кроме того, требование возможности выбираемого направления может приводить к отклонению от направления скорейшего подъема, что может в принципе уменьшить скорость приближения к решению. Таким образом, скорость сходимости в методах возможных направлений не выше, чем в градиентных методах безусловной оптимизации.
Следует отметить также, что недостатком методов возможных направлений является необходимость решения подзадач линейного программирования.
