- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
Метод Хука-Дживса
Этот метод был разработан в 1961 году для решения задачи (12.1). Метод Хука-Дживса представляет собой последовательность двух процедур: исследующего поиска (ИП) вокруг текущей базисной точки и поиска по образцу (ПО).
Исследующий
поиск (ИП). Для проведения ИП (рис. 12.1.)
необходимо задать исходную базисную
точку
![]() ,
шаг
,
шаг
![]() для каждой переменной
для каждой переменной
![]()
![]() ,
-
коэффициент уменьшения шага
,
-
коэффициент уменьшения шага
![]() в процессе поиска. Каждая переменная
(координата) по очереди изменяется на
величину шага
в процессе поиска. Каждая переменная
(координата) по очереди изменяется на
величину шага
![]() и вычисляется
и вычисляется
![]() ,
где
,
где
![]() -j-ый
единичный вектор
.
Если
-j-ый
единичный вектор
.
Если
![]() ,
то
,
то
![]() заменяется на
заменяется на
![]() .
В противном случае делается шаг в
противоположном направлении, т.е.
вычисляется
.
В противном случае делается шаг в
противоположном направлении, т.е.
вычисляется
![]() .
Если это приводит к уменьшению значения
функции, то
.
Если это приводит к уменьшению значения
функции, то
![]() заменяется на
заменяется на
![]() ;
иначе точка
не заменяется. После перебора всех n
координат ИП вокруг точки
;
иначе точка
не заменяется. После перебора всех n
координат ИП вокруг точки
![]() завершается получением новой базисной
точки
завершается получением новой базисной
точки
![]() .
Если новая базисная точка
.
Если новая базисная точка
![]() ,
производится поиск по образцу, иначе
ИП повторяется вокруг точки
,
производится поиск по образцу, иначе
ИП повторяется вокруг точки
![]() ,
но с уменьшенным шагом.
,
но с уменьшенным шагом.
Алгоритм исследующего поиска вокруг текущей базисной точки x
Начальный
этап. Задать точку
,
систему линейно-независимых направлений
![]() ,
шаг
,
шаг
![]() ;
положить
;
положить
![]() ,
,
![]() ;
.
;
.
Основной этап.
Вычислить
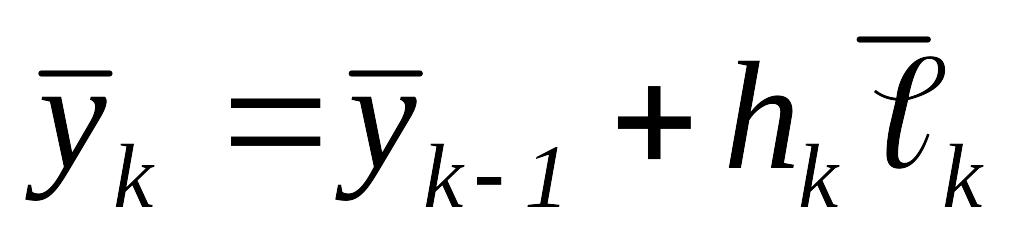 ,
,
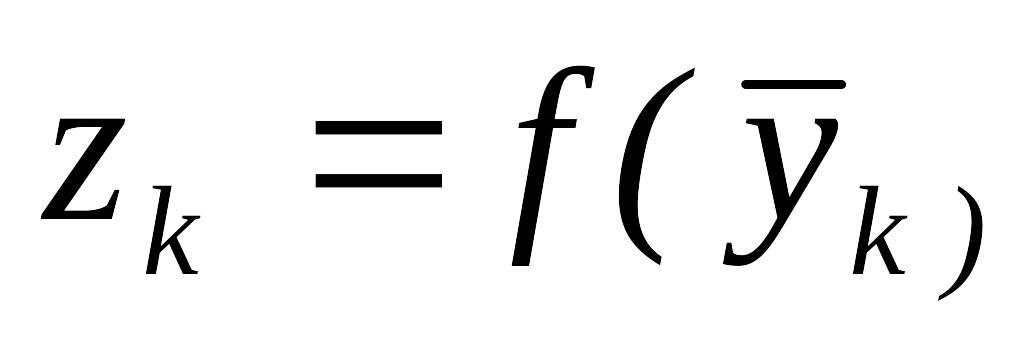 .
.Если
 ,
то перейти к шагу 5.
,
то перейти к шагу 5.Вычислить
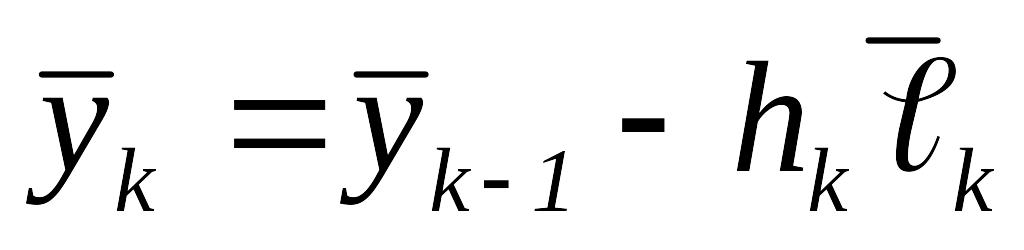 ,
,
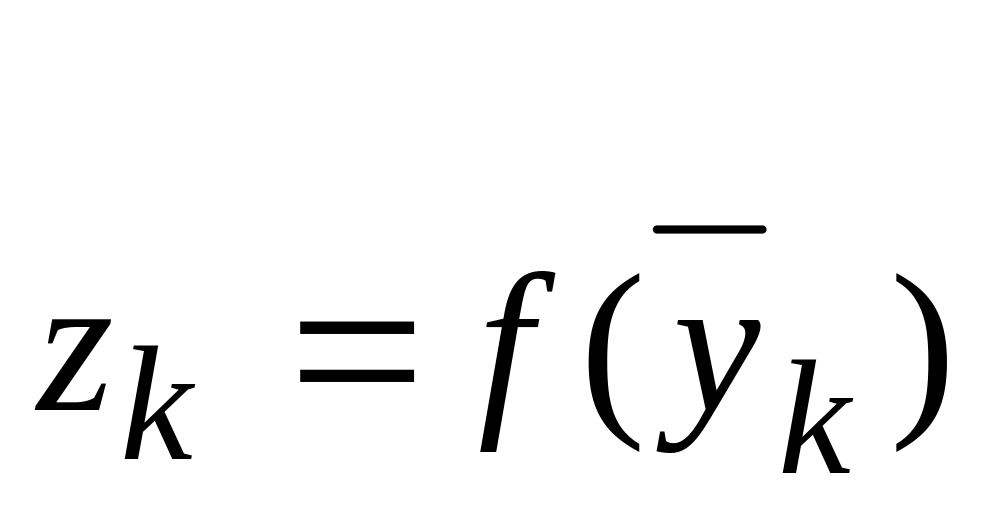 .
.Если , то перейти к шагу 5, иначе положить
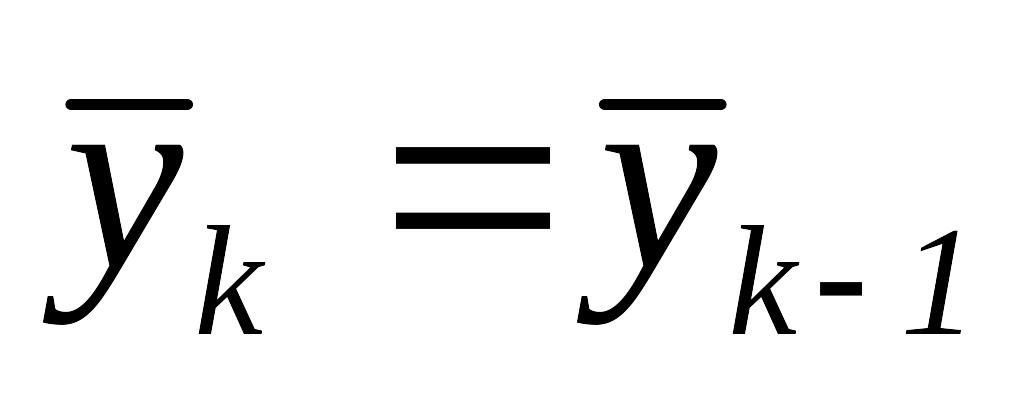 ,
,
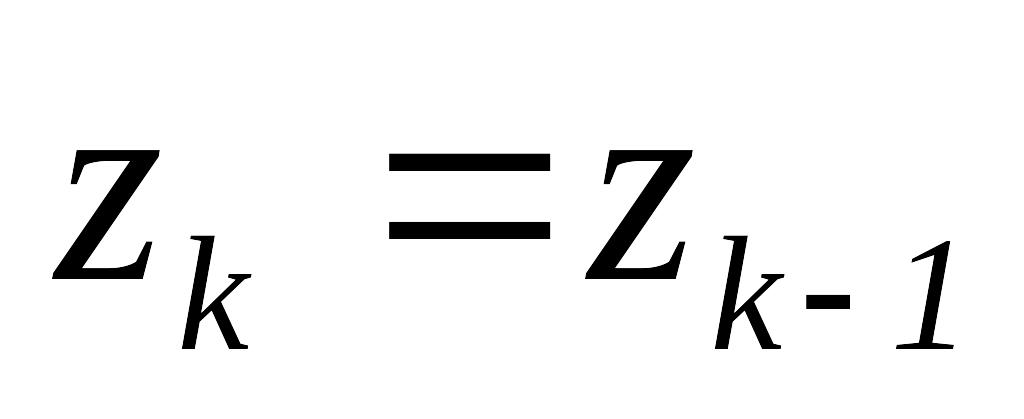 .
.Если
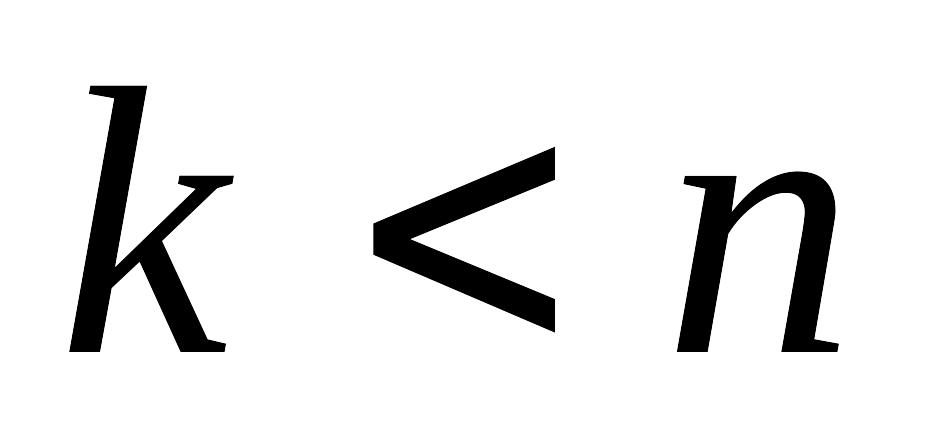 ,
то положить
и перейти к шагу 1, иначе положить
,
то положить
и перейти к шагу 1, иначе положить
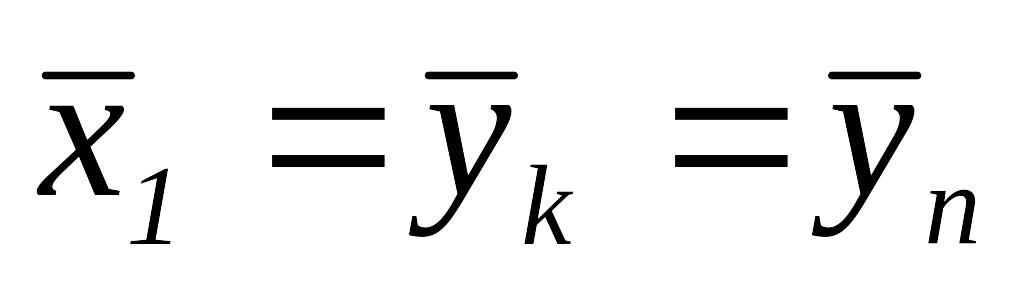 и остановиться.
и остановиться.
Поиск
по образцу (ПО) заключается в нахождении
точки
![]() ,
лежащей на направлении, соединяющем
две соседние базисные точки
и
,
лежащей на направлении, соединяющем
две соседние базисные точки
и
![]() :
:
![]() .
.
Далее
проводится ИП вокруг точки
,
приводящий в точку
![]() .
Если
.
Если
![]() ,
то точка
,
то точка
![]() принимается за новую базисную точку
принимается за новую базисную точку
![]() и вновь производится ПО, но уже в
направлении
и вновь производится ПО, но уже в
направлении
![]() ,
в противном случае нужно вернуться в
точку
и провести ИП вокруг нее с целью построения
нового направления движения по образцу.
Если ИП вокруг текущей базисной точки
не приводит к успеху
,
в противном случае нужно вернуться в
точку
и провести ИП вокруг нее с целью построения
нового направления движения по образцу.
Если ИП вокруг текущей базисной точки
не приводит к успеху
![]() ,
т.е. значение функции
не уменьшается при движении вдоль любых
координат осей, то необходимо уменьшить
величину шага
вдоль каждой из осей и провести ИП
заново. Решение задачи завершается,
когда величина шага (
,
т.е. значение функции
не уменьшается при движении вдоль любых
координат осей, то необходимо уменьшить
величину шага
вдоль каждой из осей и провести ИП
заново. Решение задачи завершается,
когда величина шага (![]() )
становится достаточно малой.
)
становится достаточно малой.
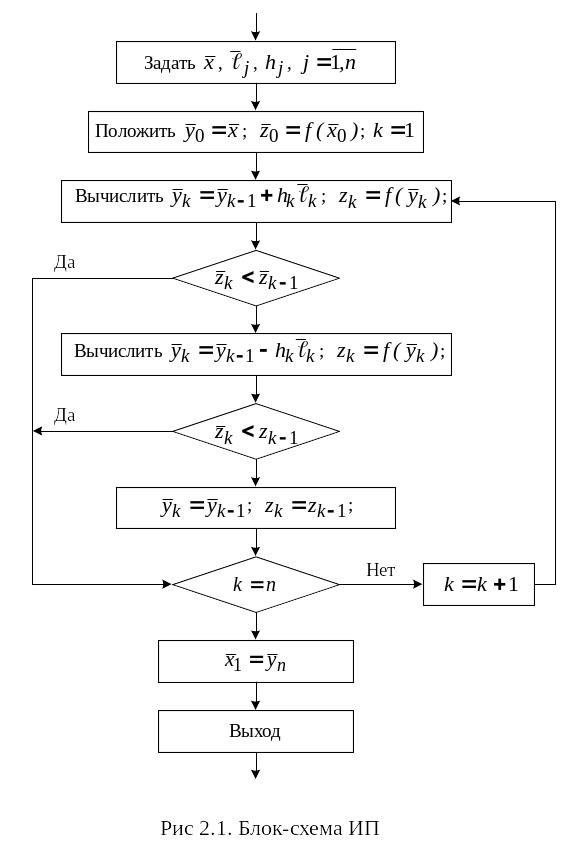
Алгоритм метода Хука-Дживса
Начальный
этап. Задать начальную точку
![]() ,начальный
вектор приращения
,начальный
вектор приращения
![]() ,
,
![]() – коэффициент уменьшения шага,
– коэффициент уменьшения шага,
![]() – параметр окончания счета, положить
.
– параметр окончания счета, положить
.
Основной этап.
Провести ИП вокруг точки ; – полученная в результате точка.
Если
 ,
то перейти к шагу 4.
,
то перейти к шагу 4.Если
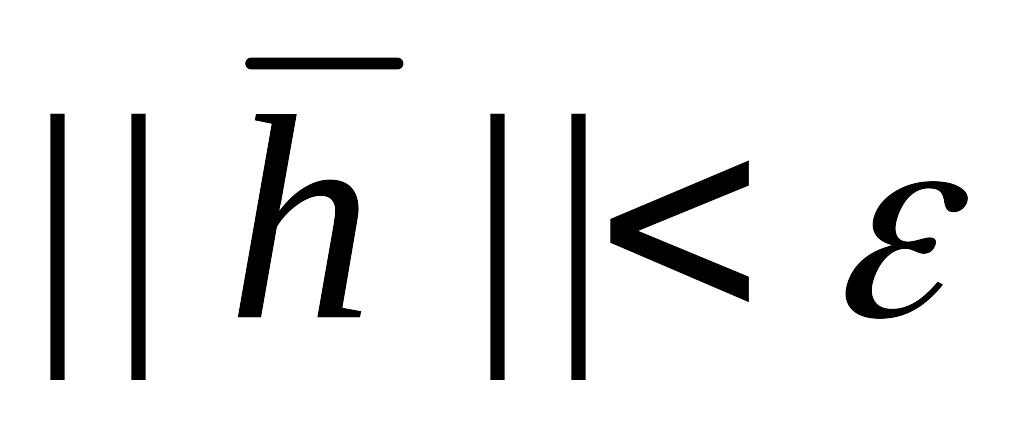 ,
то положить
и остановиться, иначе положить
,
то положить
и остановиться, иначе положить
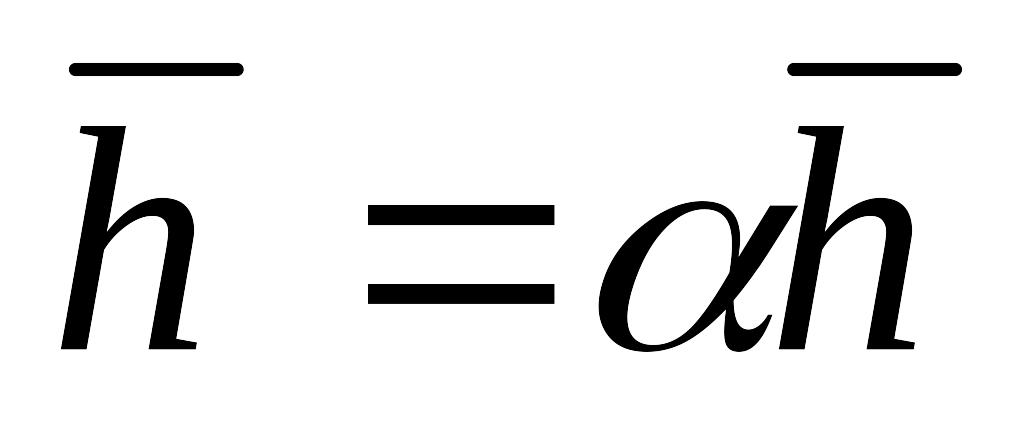 и перейти к шагу 1.
и перейти к шагу 1.Вычислить .
Провести ИП вокруг точки
 ;
;
 – полученная в результате точка.
– полученная в результате точка.Если
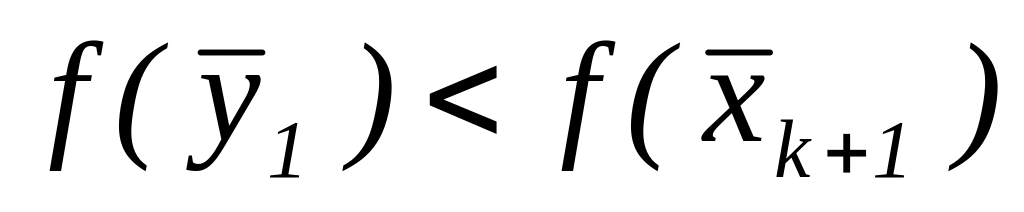 ,
то положить
,
то положить
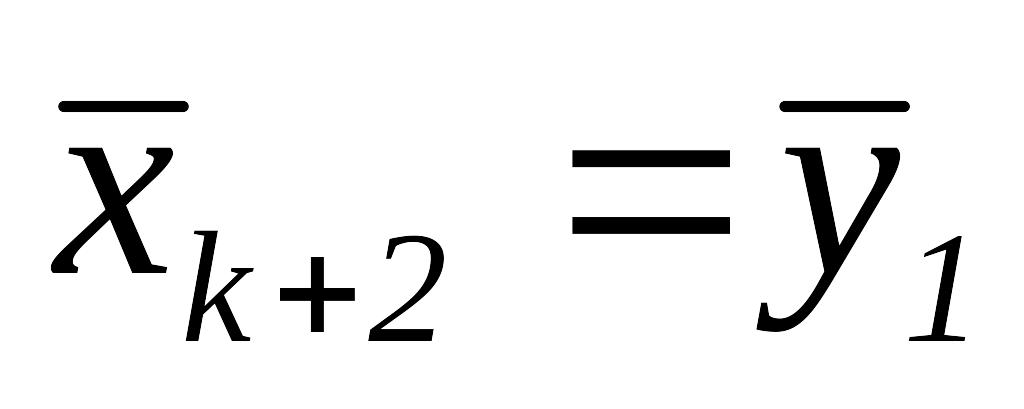 ,
и перейти к шагу 3.
,
и перейти к шагу 3.
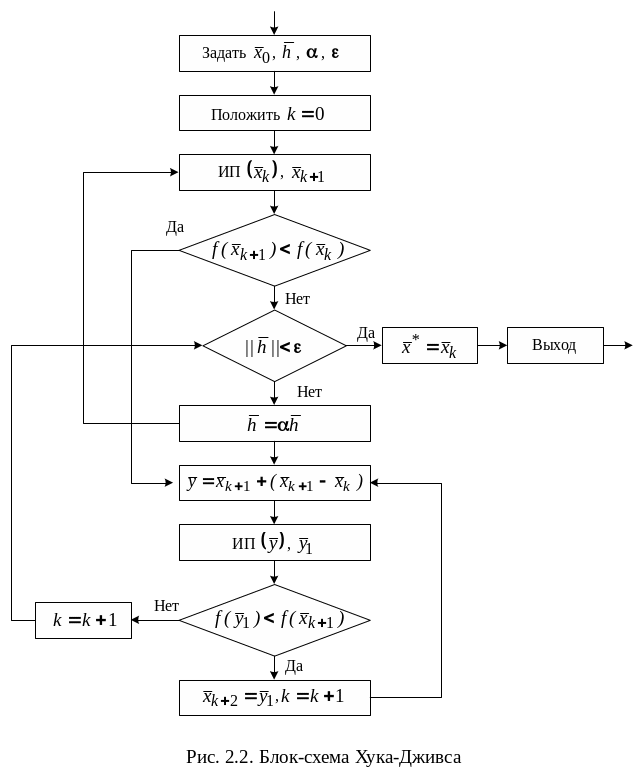
На рис 12.2 приведена блок-схема алгоритма.
Пример
12.1. Найти точку минимума функции
![]() .
.
Очевидно,
что оптимальной является точка
![]() ,
в которой
,
в которой
![]() .
.
Начальный
этап. Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Основной этап.
ИП вокруг ,
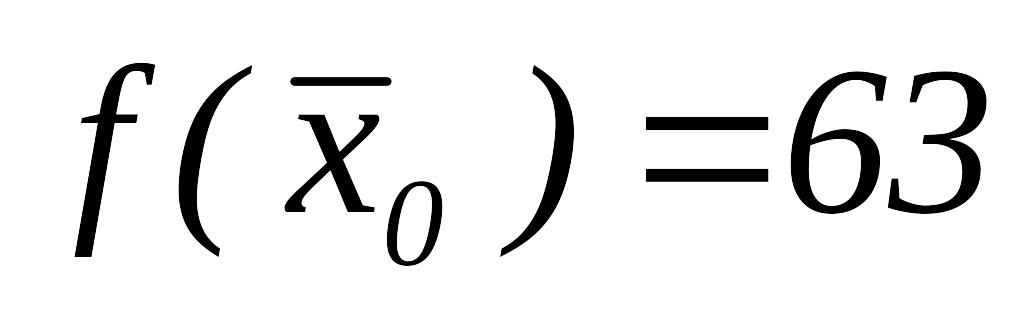 .
Полагаем
.
Полагаем
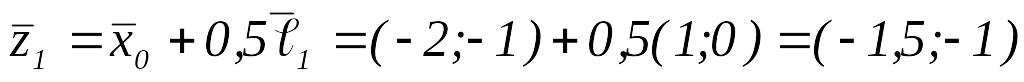 ,
,
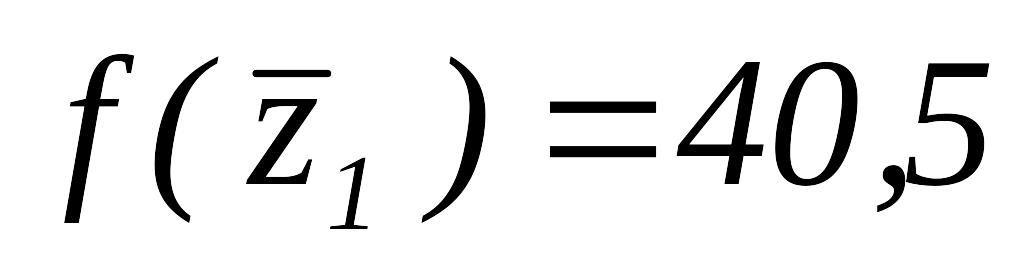 .
Так как
.
Так как
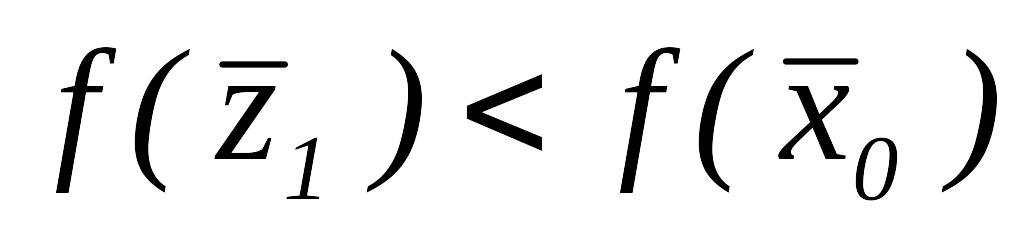 ,
вычисляем
,
вычисляем
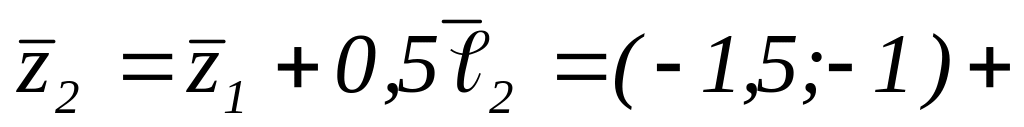
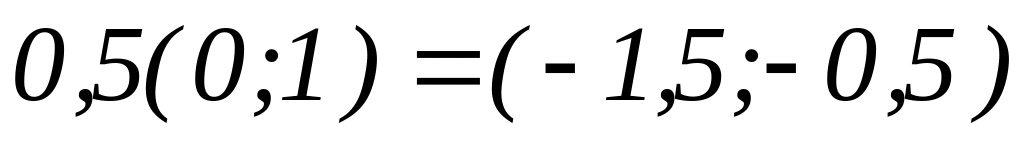 ,
,
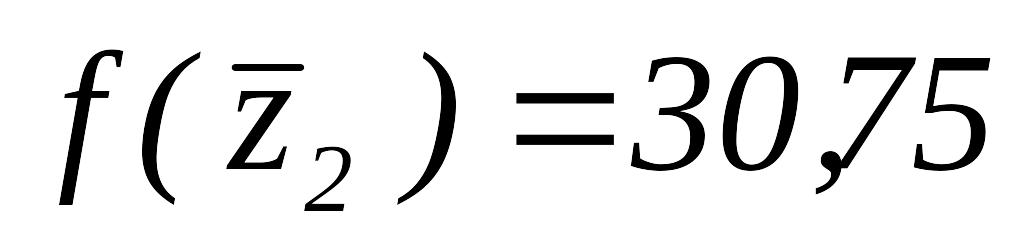 .
Так как
.
Так как
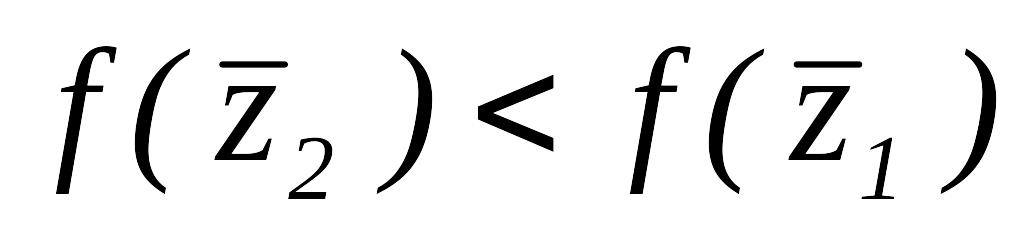 ,
то
,
то
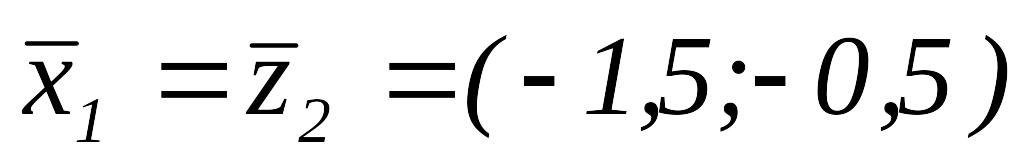 .
.Так как
 ,
то
,
то
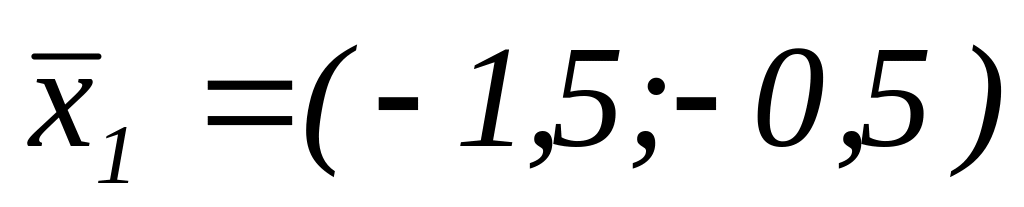 – новая базисная точка.
– новая базисная точка.
ПО. Вычисляем
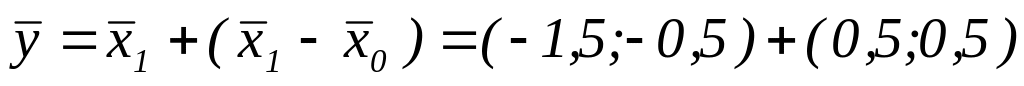 =
=
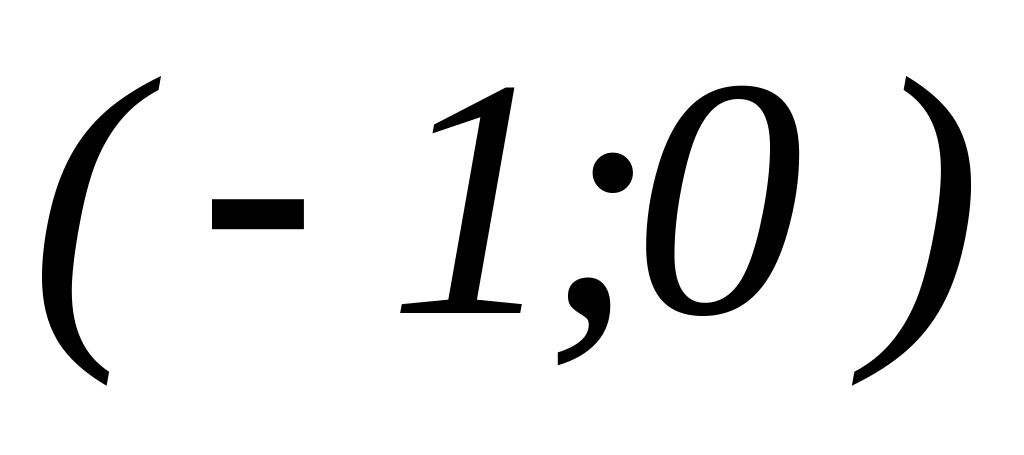 .
.ИП вокруг
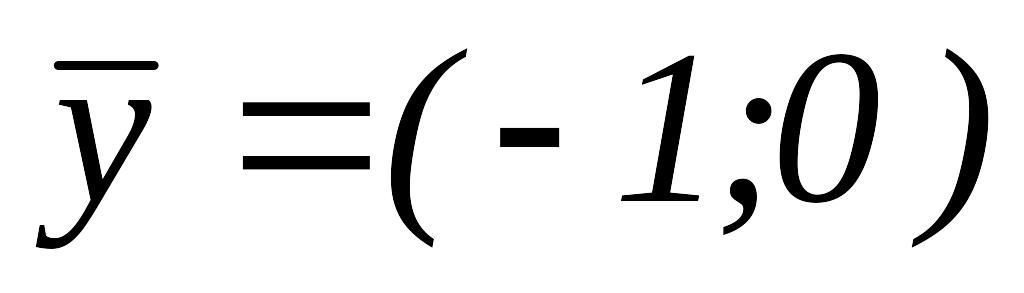 ,
,
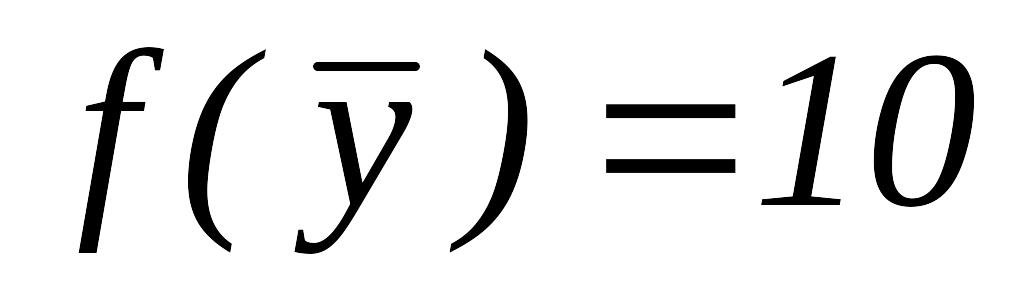 .
Вычисляем
.
Вычисляем
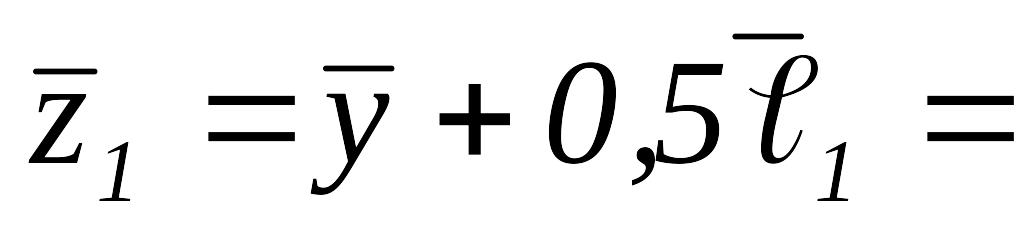
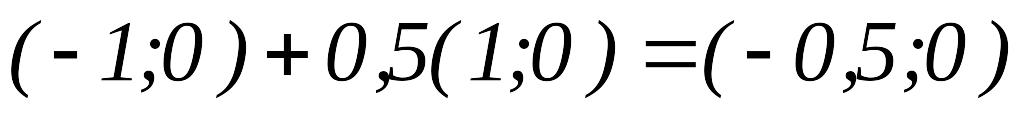 ,
,
 .
Так как
.
Так как
 ,
вычисляем
,
вычисляем
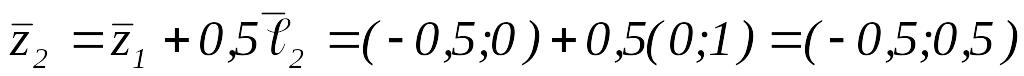 ,
,
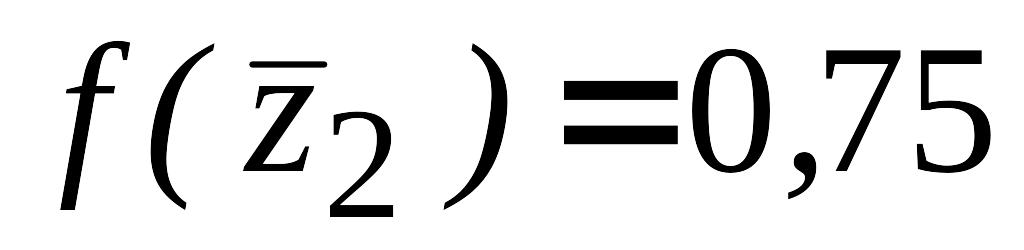 .
Так как
.
Так как
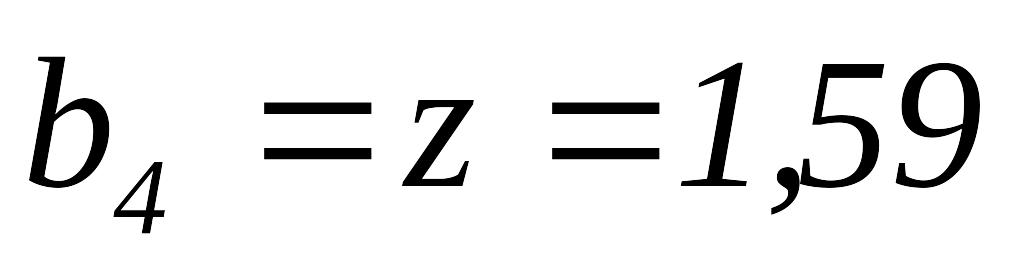 ,
то
,
то
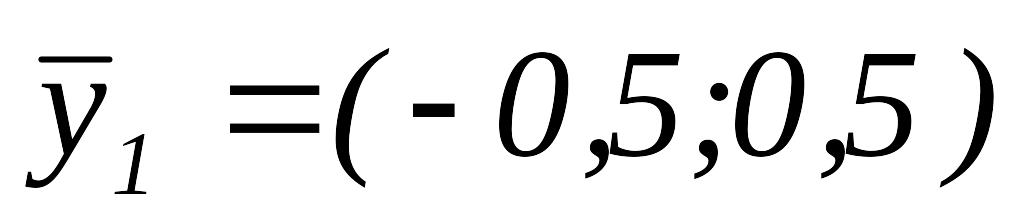 .
.Так как
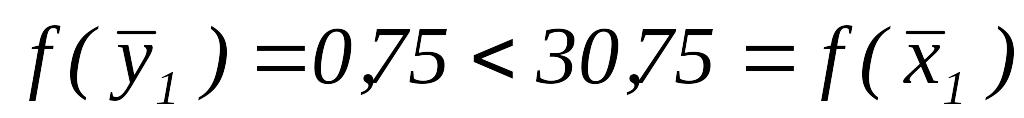 ,
полагаем
,
полагаем
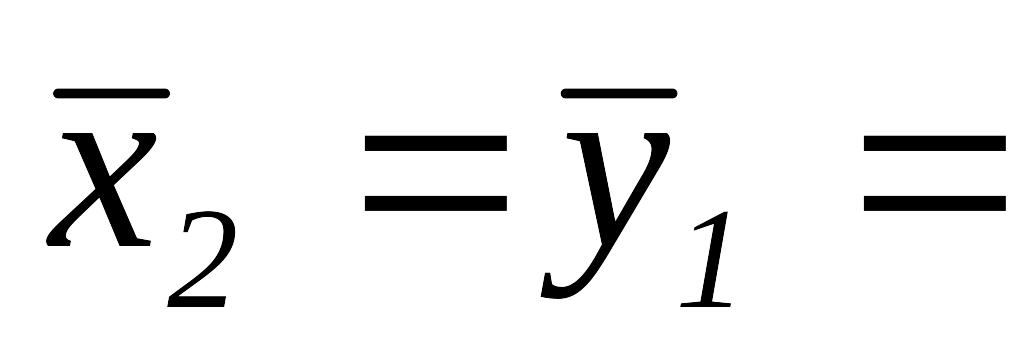
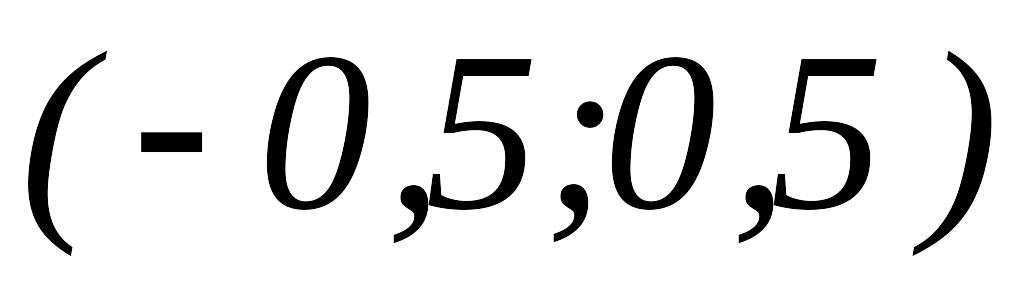 ,
,
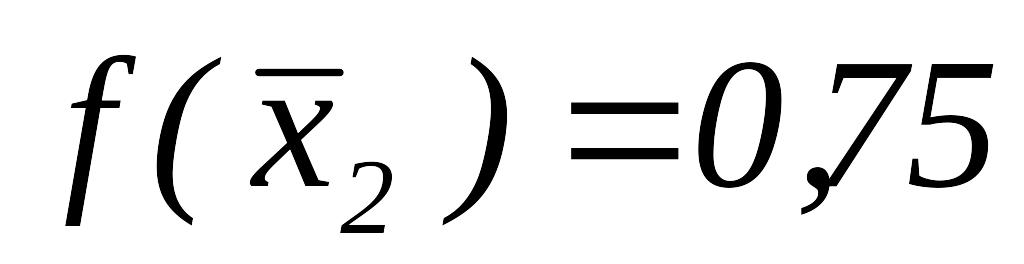 и переходим опять к ПО при
и переходим опять к ПО при
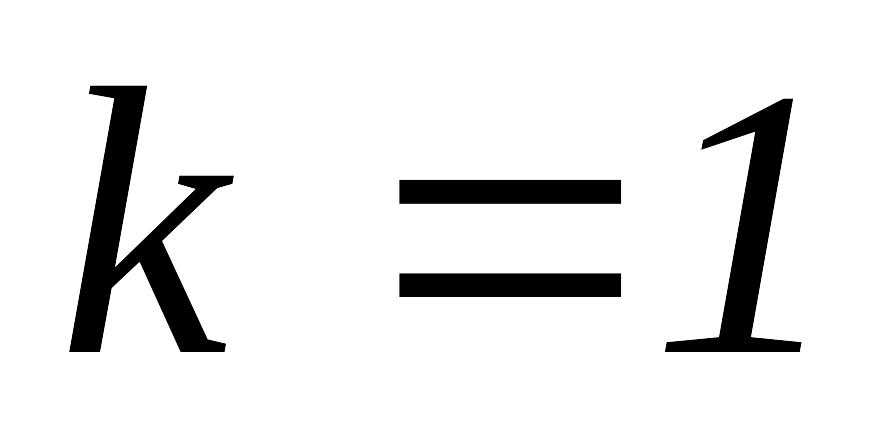 .
.
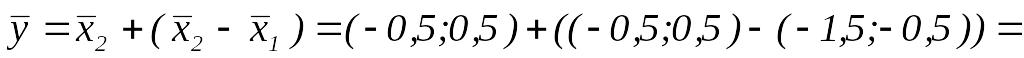
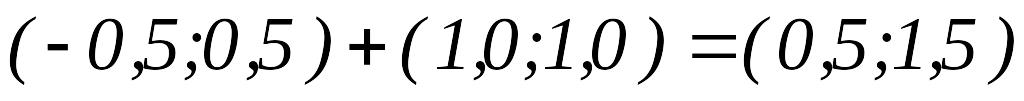 ,
,
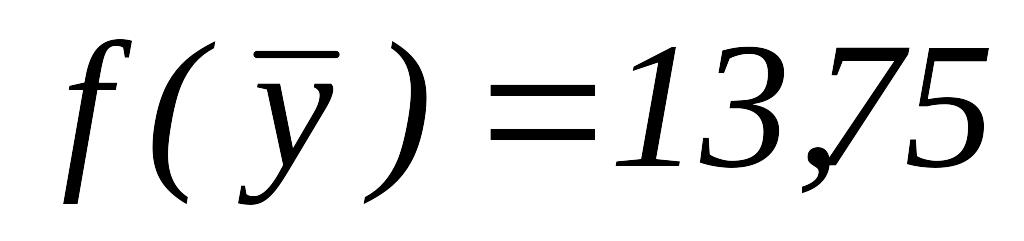 .
.ИП вокруг
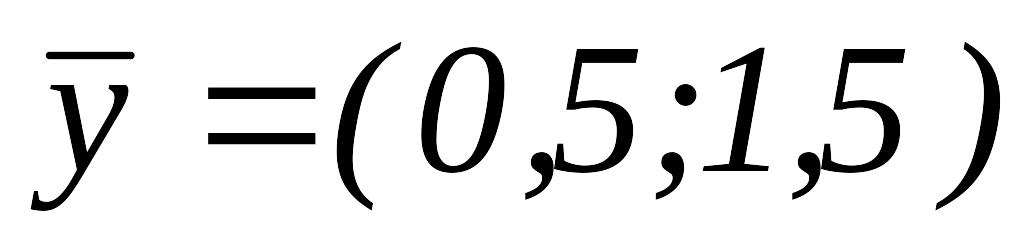 ,
.
Вычисляем
,
.
Вычисляем
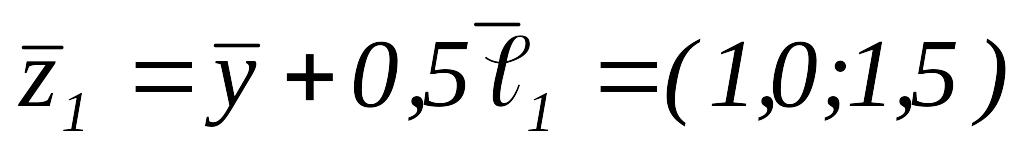 .
Так как
.
Так как
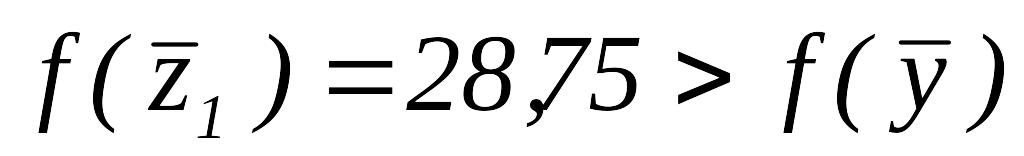 ,
полагаем
,
полагаем
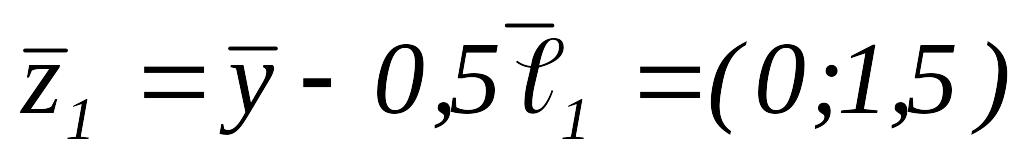 ,
Так как
,
Так как
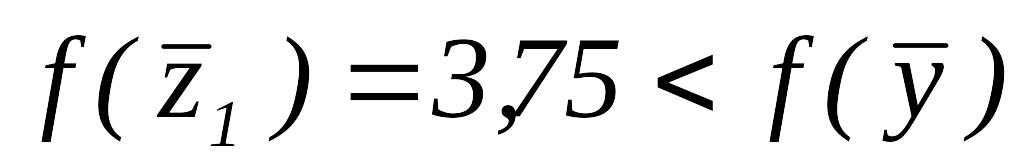 ,
вычисляем
,
вычисляем
 .
Так как
.
Так как
 ,
вычисляем
,
вычисляем
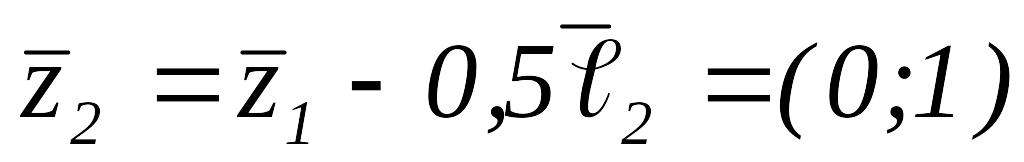 .
Так как
.
Так как
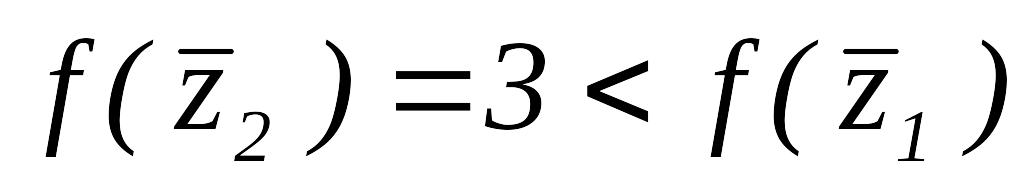 ,
то
,
то
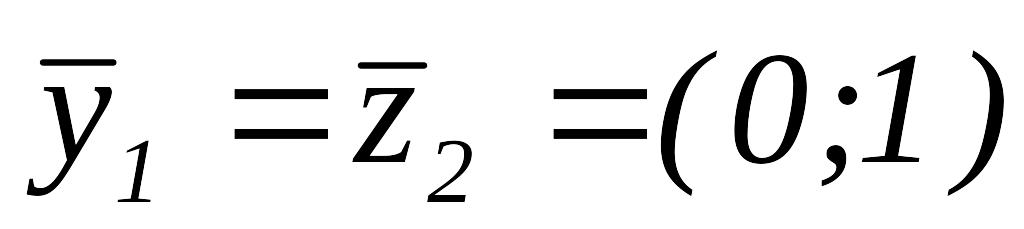 .
.Так как
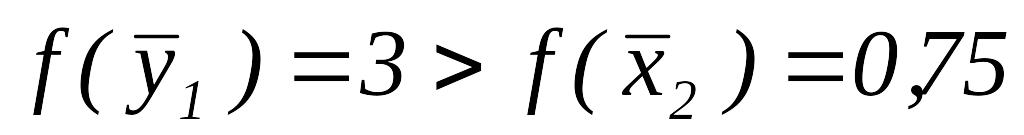 ,
полагаем
,
полагаем
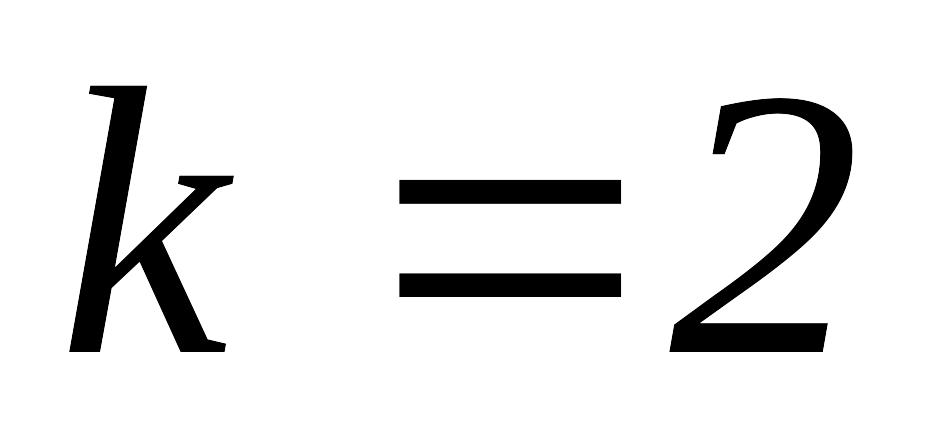 и переходим к шагу 3, не меняя базисной
точки, т.к. поиск ПО был неудачным.
и переходим к шагу 3, не меняя базисной
точки, т.к. поиск ПО был неудачным.
Так как
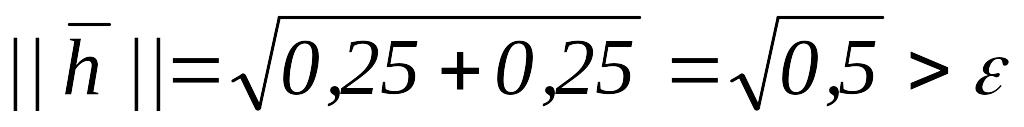 ,
то
,
то
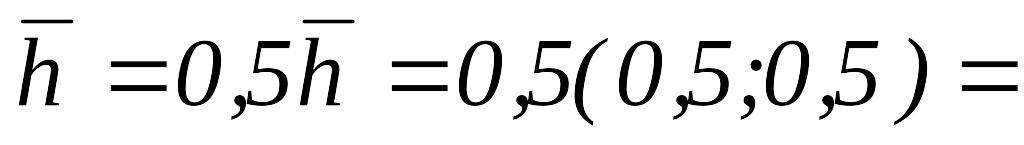
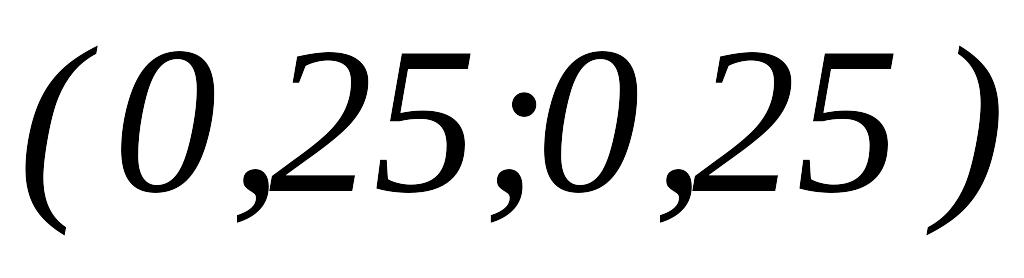 и переходим к шагу 1.
и переходим к шагу 1.
ИП вокруг точки
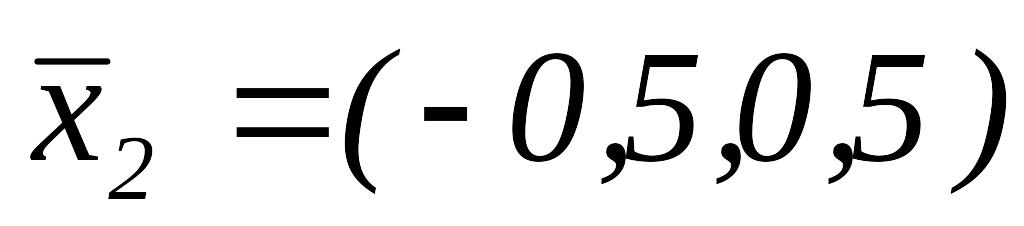 ,
.
Вычисляем
,
.
Вычисляем
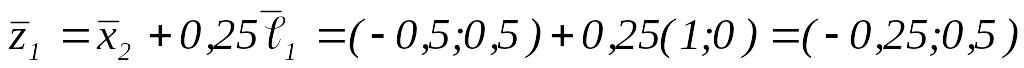 .
Так как
.
Так как
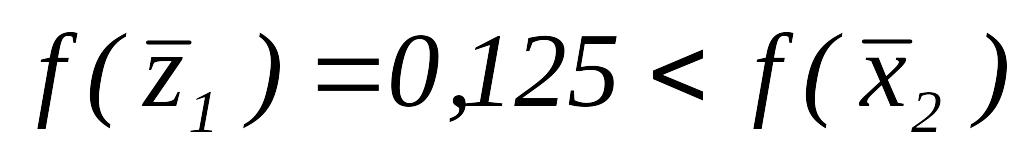 ,
полагаем
,
полагаем
 .
Так как
.
Так как
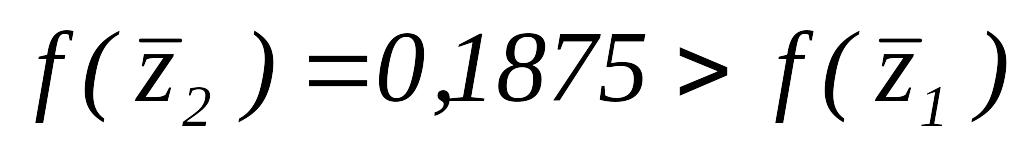 ,
то полагаем
,
то полагаем
 и
и
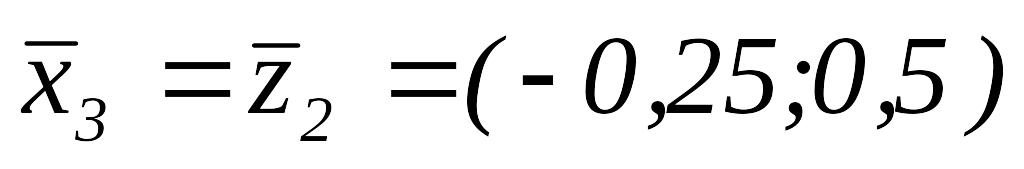 ,
,
 .
.Так как
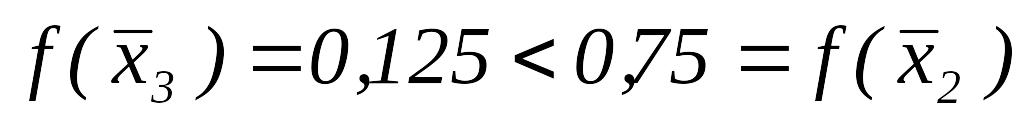 ,
переходим к шагу 4.
,
переходим к шагу 4.
ПО.
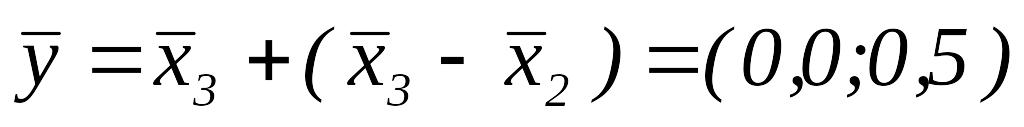 ,
,
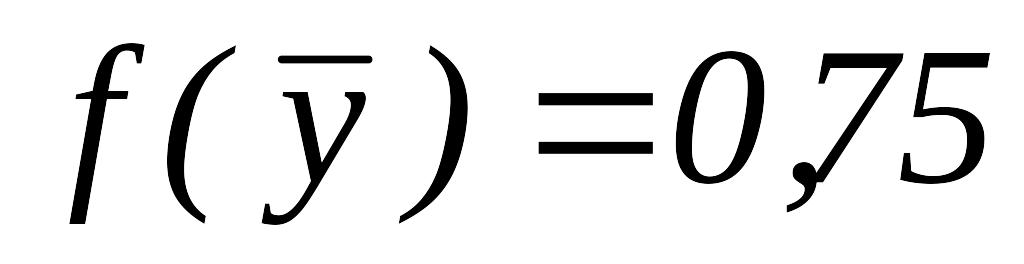 .
.ИП вокруг
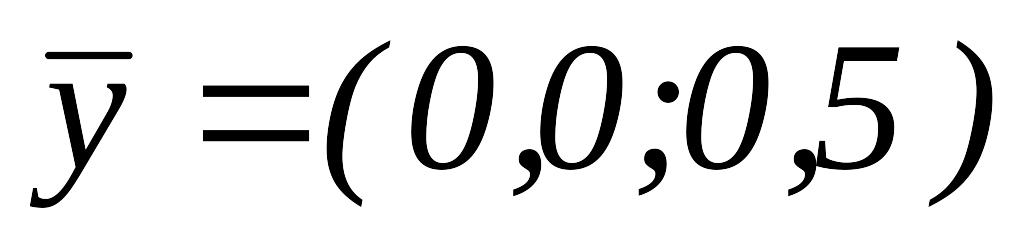 .
Вычисляем
.
Вычисляем
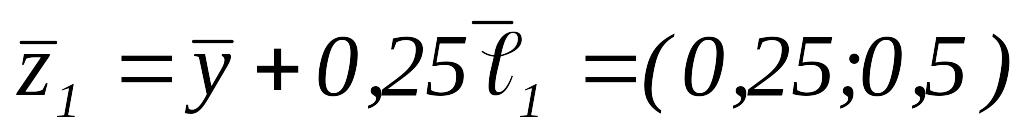 .
Так как
.
Так как
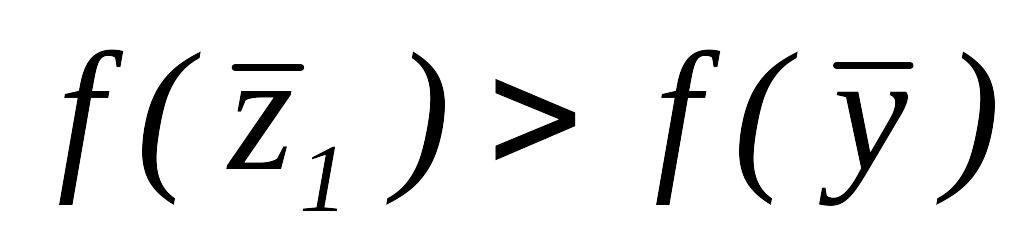 ,
то вычисляем
,
то вычисляем
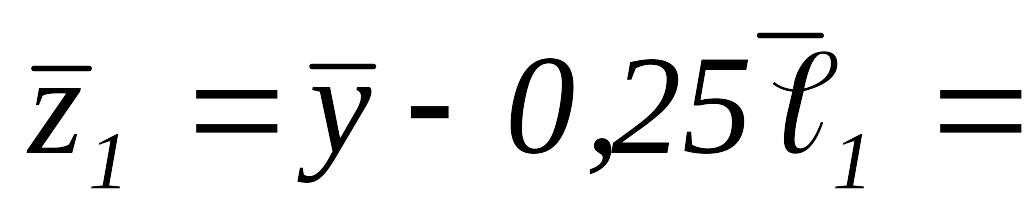
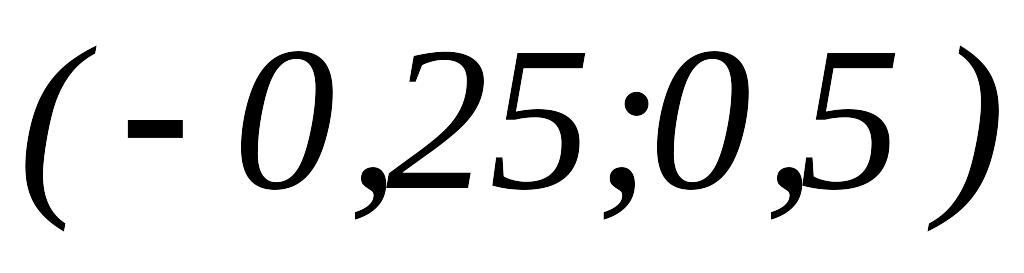 .
Так как
.
Так как
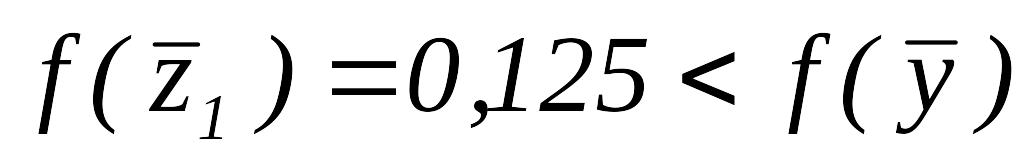 ,
то
,
то
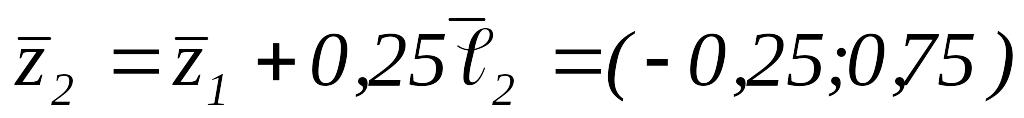 .
Так как
.
Так как
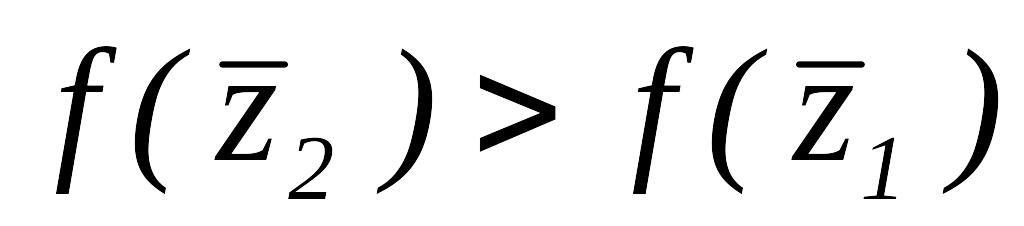 ,
то
,
то
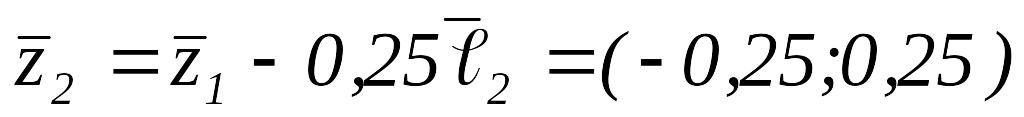 .
Так как
,
то
и
.
Так как
,
то
и
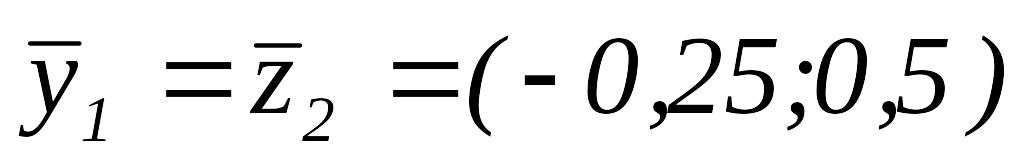 .
.Так как
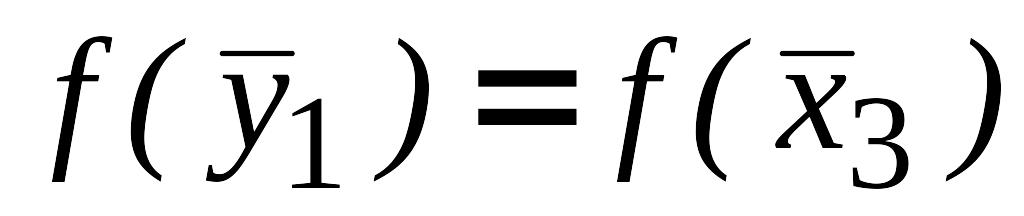 ,
полагаем
,
полагаем
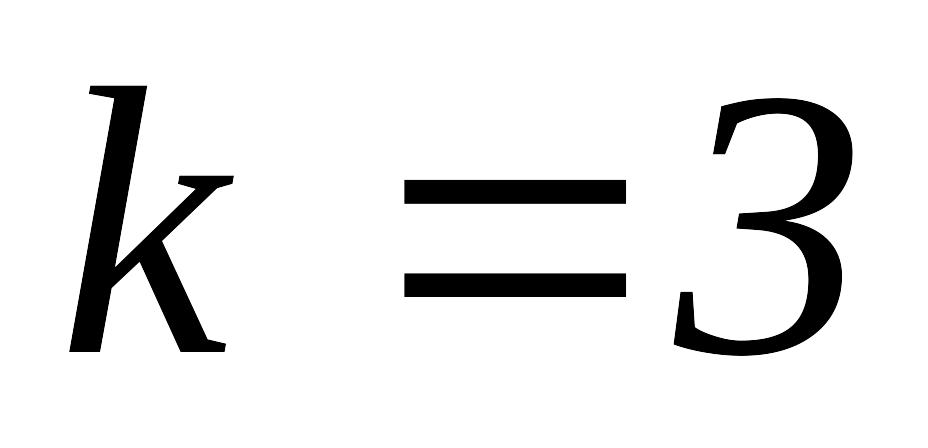 и переходим опять к шагу 3, не меняя
базисной точки.
и переходим опять к шагу 3, не меняя
базисной точки.
Так как
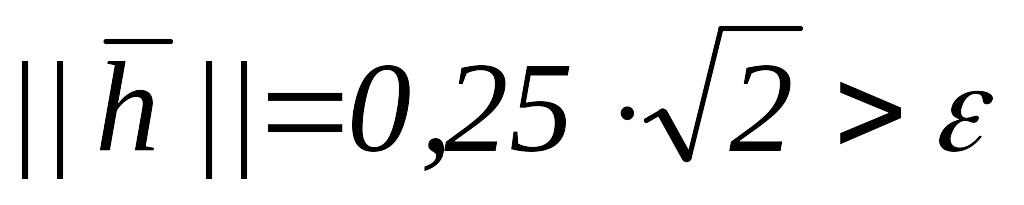 ,
то
,
то
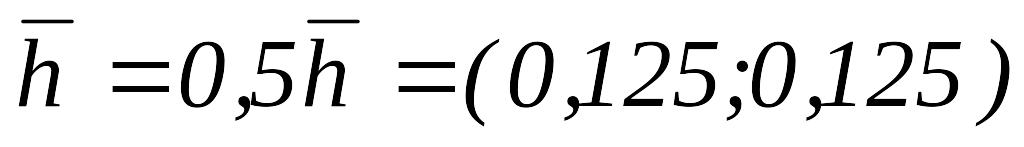 и переходим к шагу 1.
и переходим к шагу 1.
ИП вокруг точки
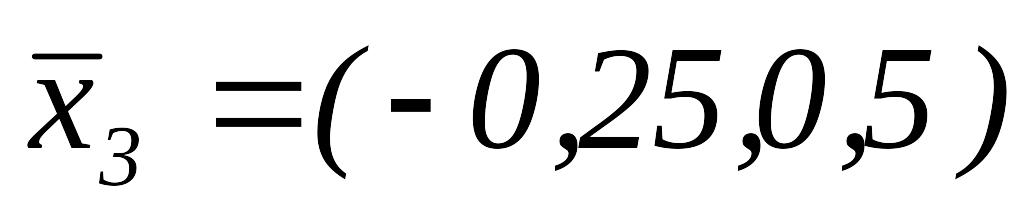 ,
.
Вычисляем
,
.
Вычисляем
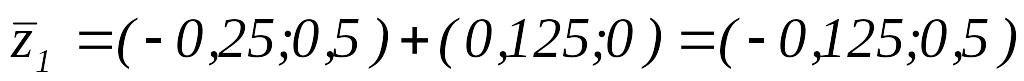 .
Так как
.
Так как
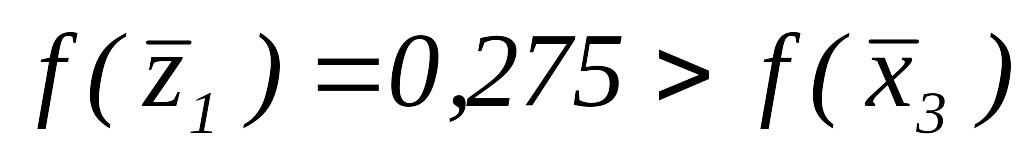 ,
то
,
то
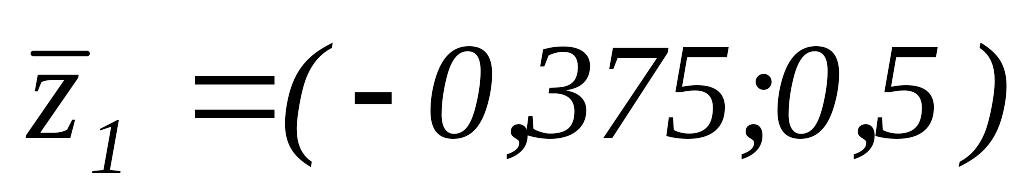 .
Так как
.
Так как
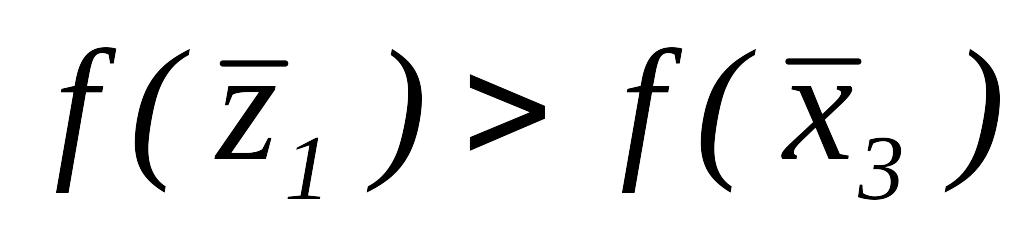 ,
то
,
то
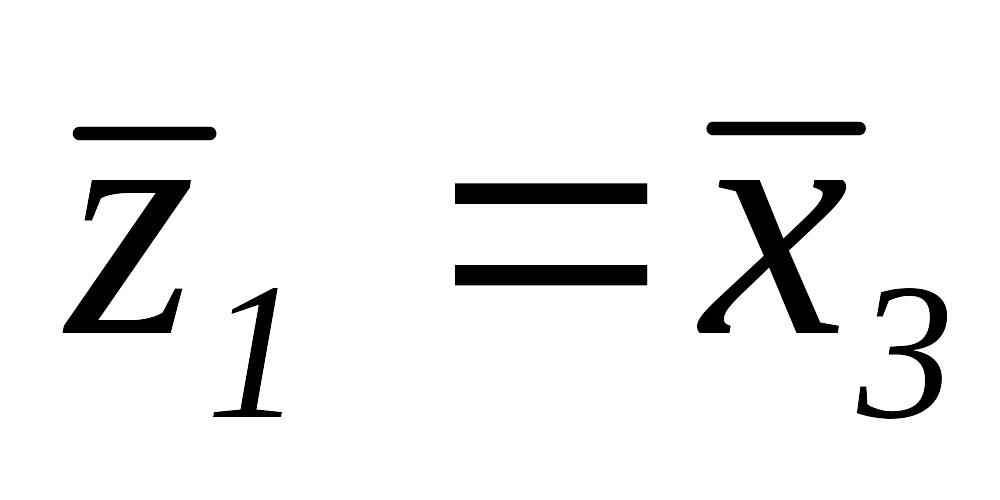 .
Далее
.
Далее
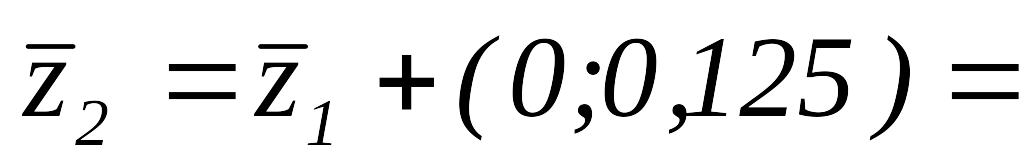
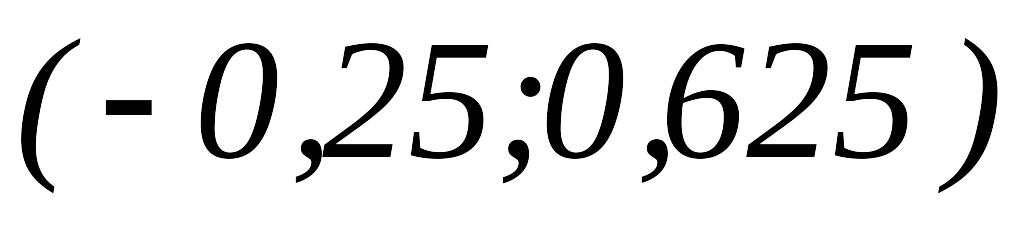 .
Так как
,
то
.
Так как
,
то
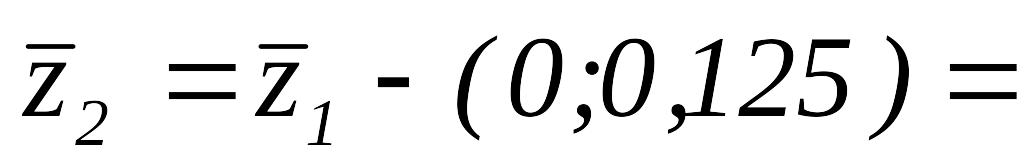
 .
Так как
,
то
.
Так как
,
то
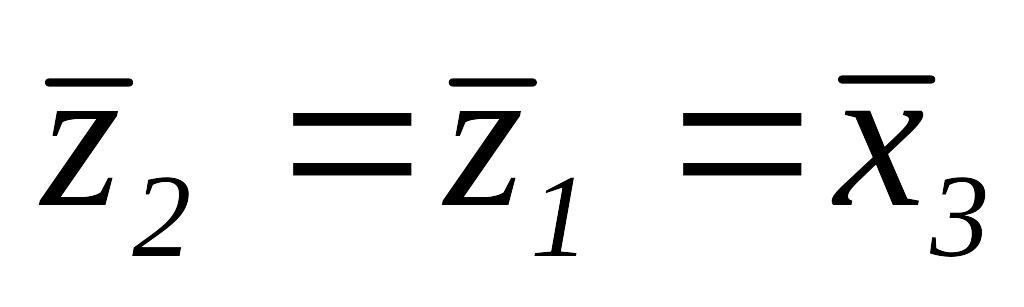 и
и
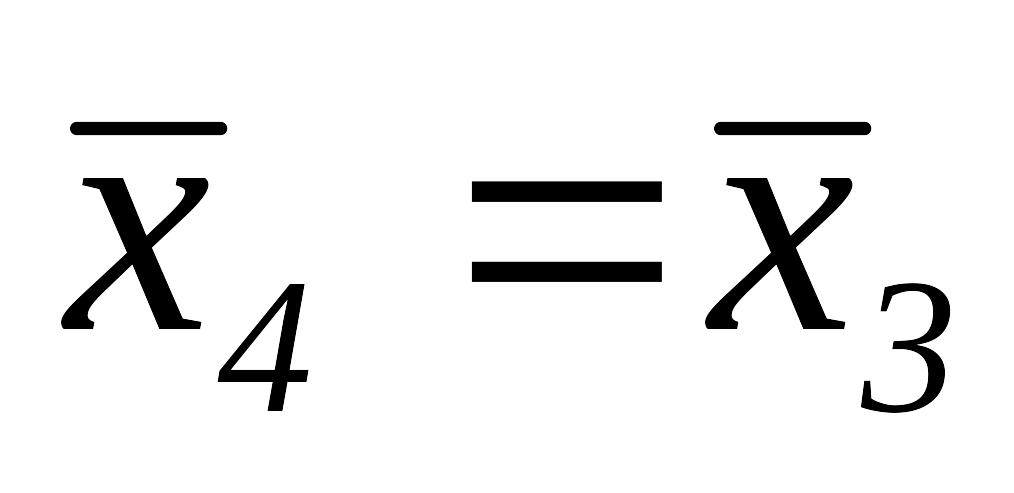 .
.Так как
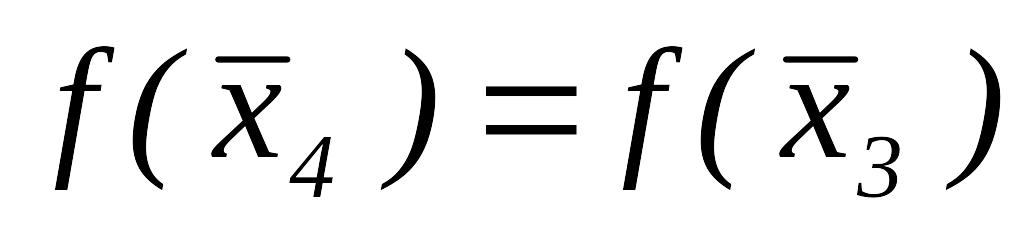 ,
то переходим к шагу 3.
,
то переходим к шагу 3.Так как
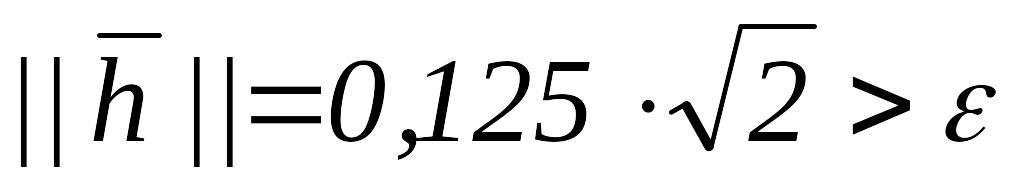 ,
то
,
то
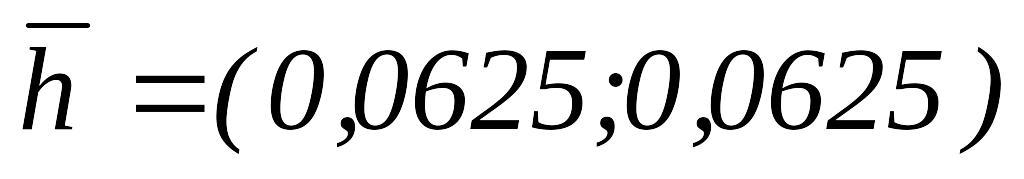 и переходим к шагу 1.
и переходим к шагу 1.
ИП вокруг точки
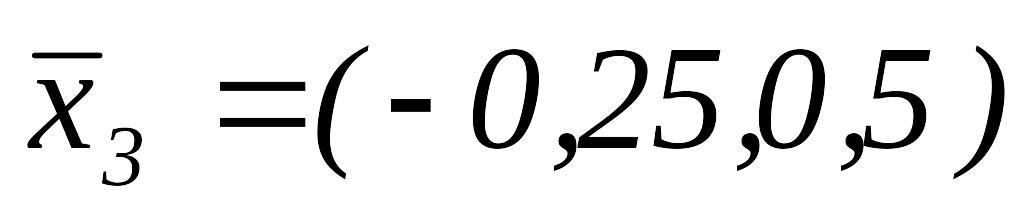 ,
.
Вычисляем
,
.
Вычисляем
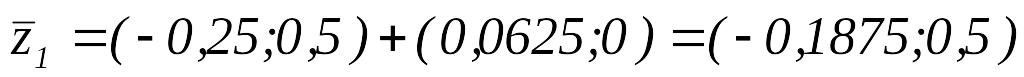 .
Так как
,
то
.
Так как
,
то
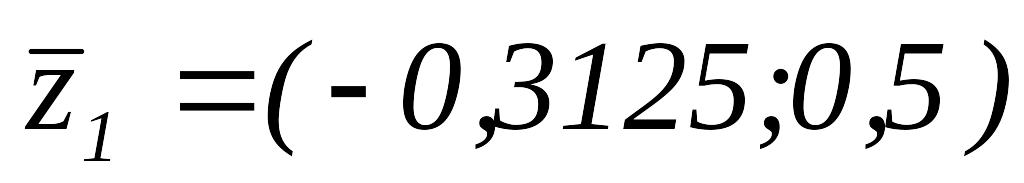 .
Так как
,
то
.
Далее
.
Так как
,
то
.
Далее
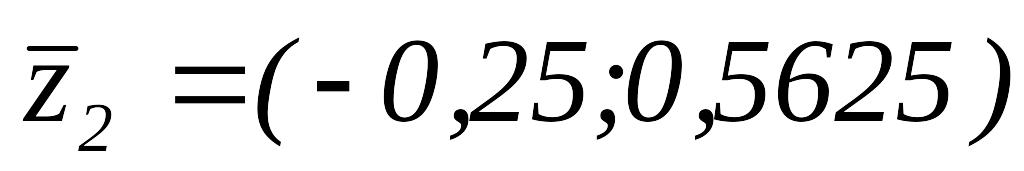 ,
,
,
,
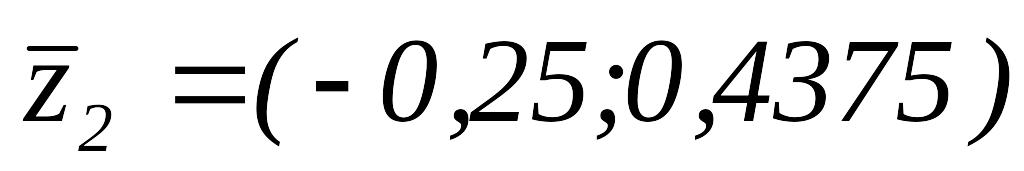 .
Так как
,
то
.
Так как
,
то
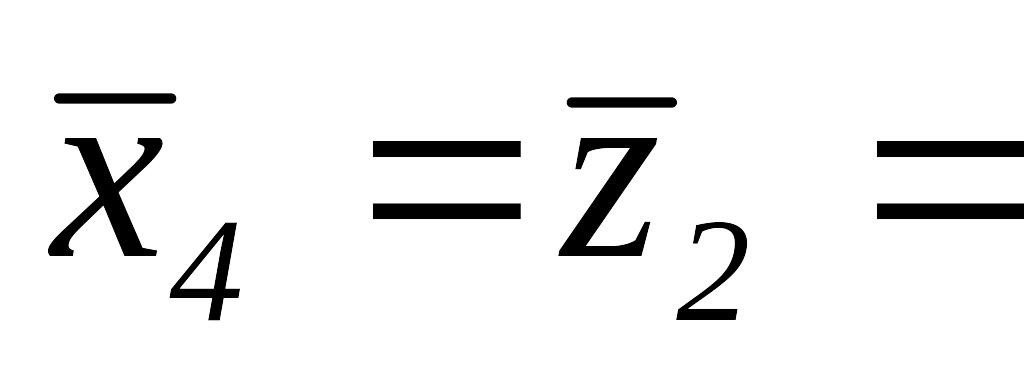
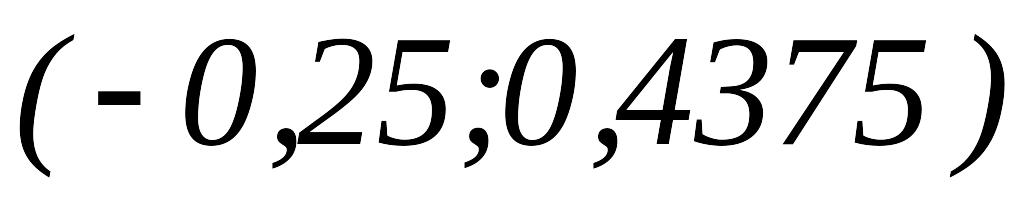 .
.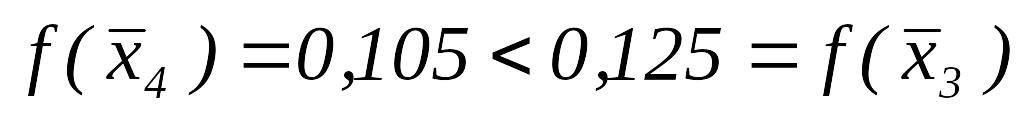 ,
то
,
то
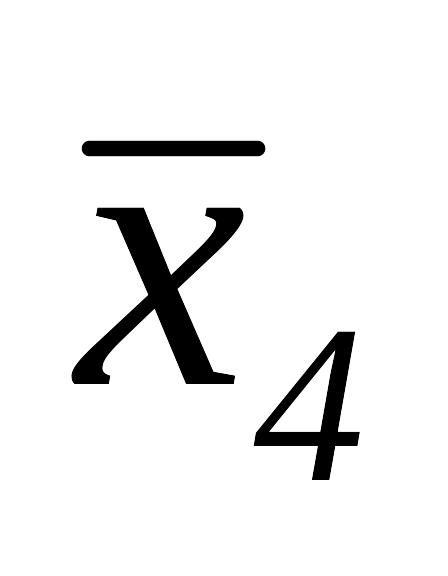 – новая базисной точки,
– новая базисной точки,
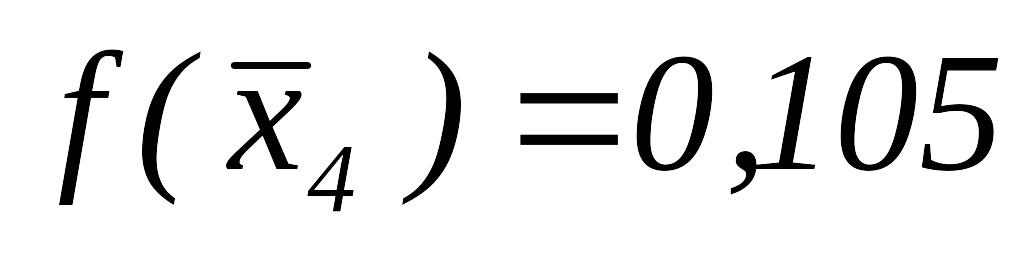 .
.
ПО.
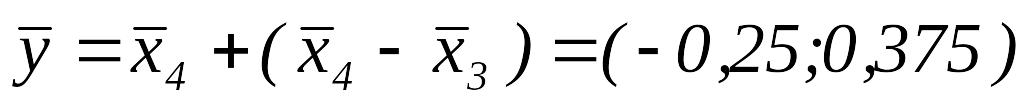 ,
,
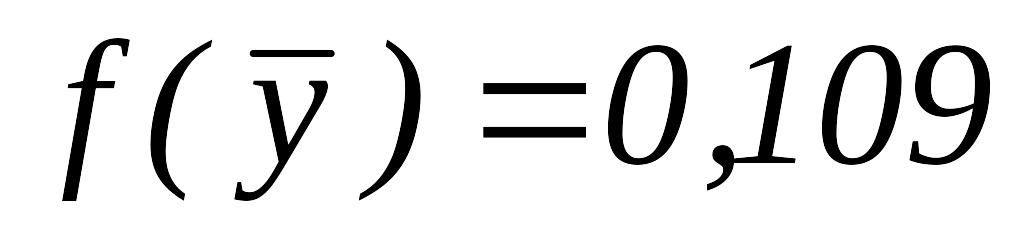 .
.ИП вокруг
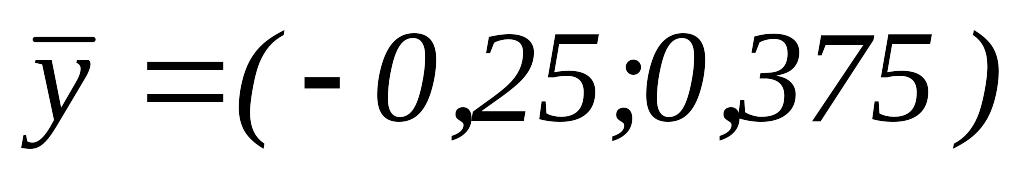 ,
.
Вычисляем
,
.
Вычисляем
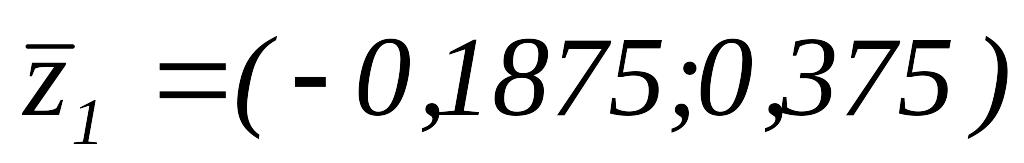 .
Так как
.
Так как
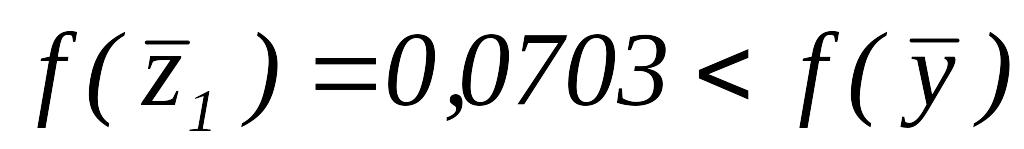 ,
то
,
то
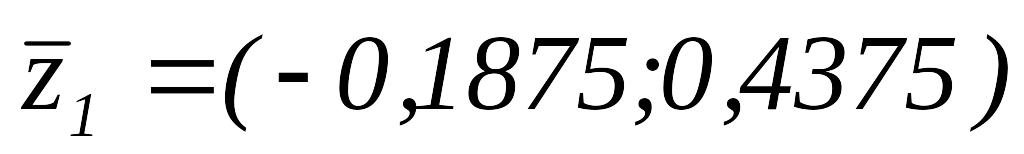 .
Так как
,
то
.
Так как
,
то
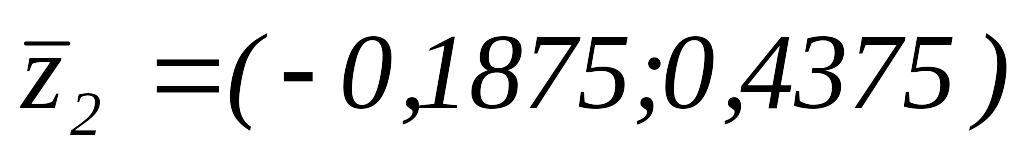 .
Так как
,
то
.
Так как
,
то
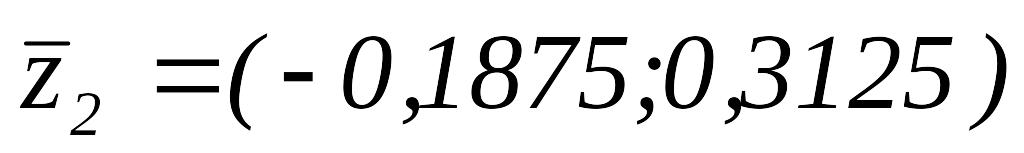 .
Так как
.
Так как
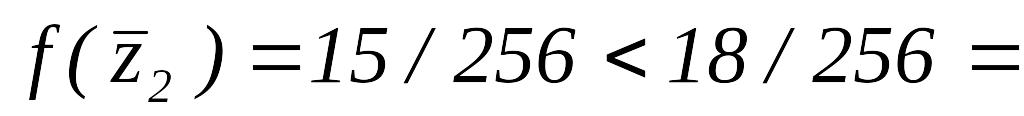
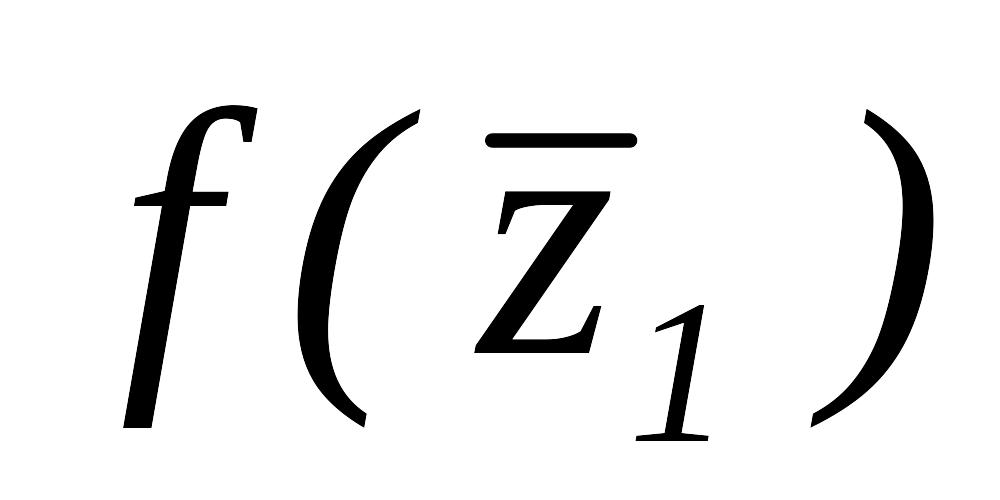 ,
следовательно
,
следовательно
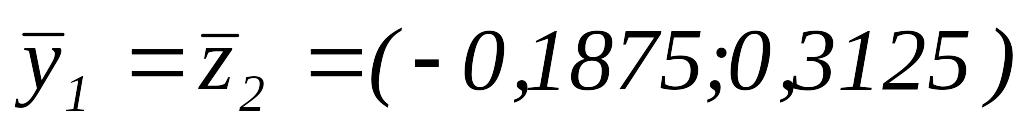 .
.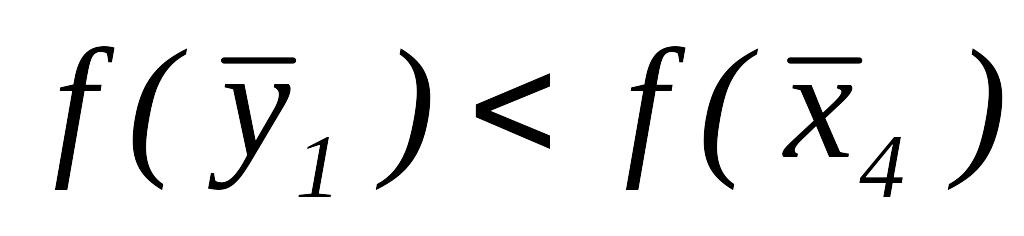 ,
поэтому полагаем
,
поэтому полагаем
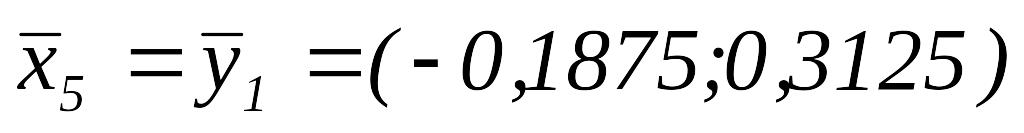 ,
,
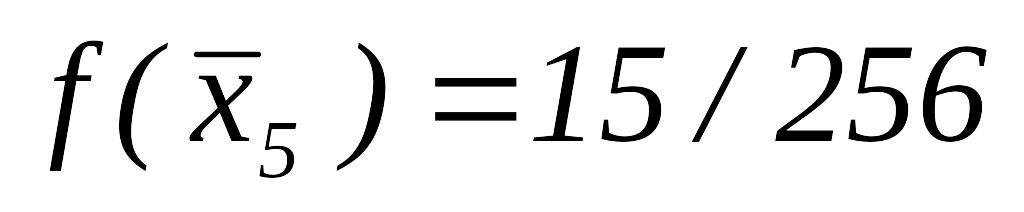 ,
,
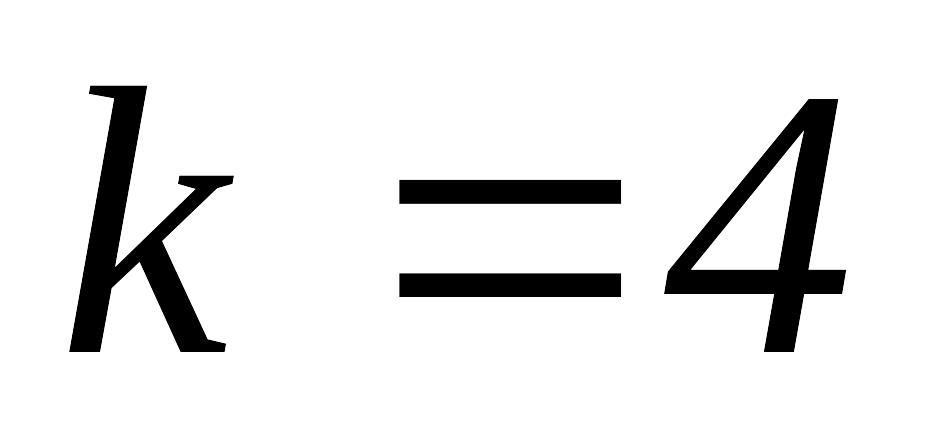 ,
переходим к шагу 4.
,
переходим к шагу 4.
ПО.
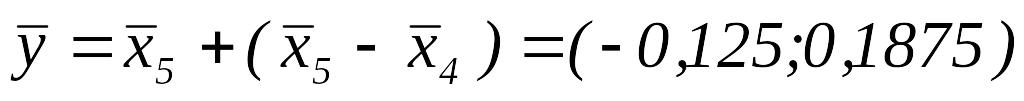 .
.ИП вокруг
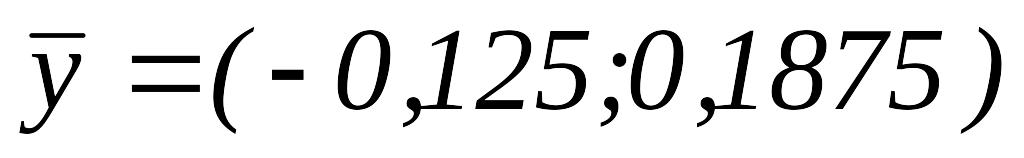 ,
,
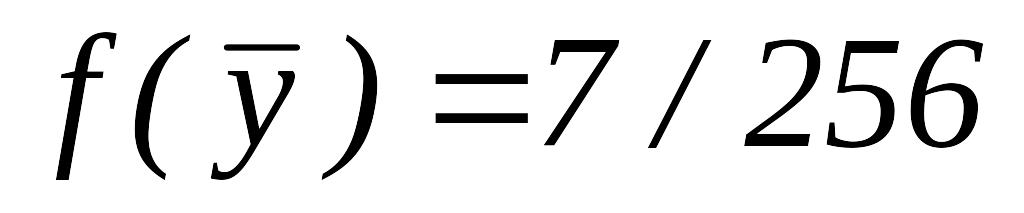 .
Вычисляем
.
Вычисляем
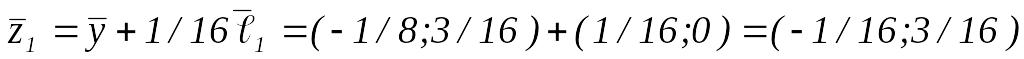 ,
,
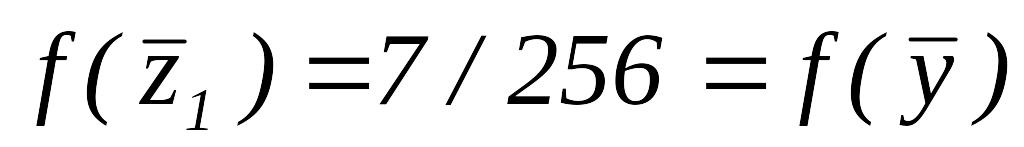 ,
тогда
,
тогда
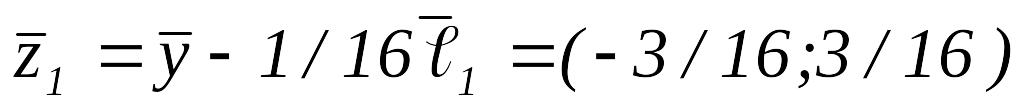 ,
,
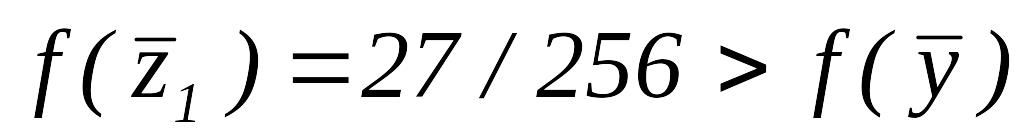 ,
т.е.
,
т.е.
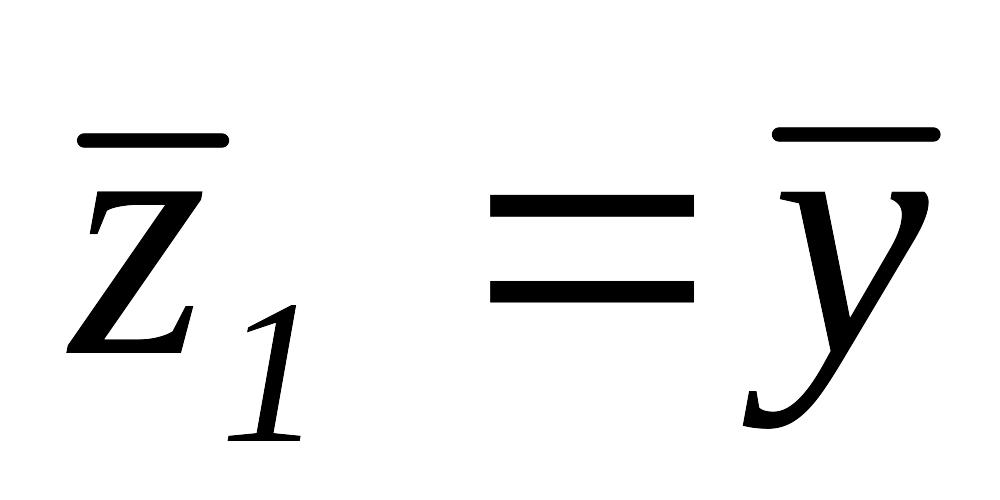 .
Далее
.
Далее
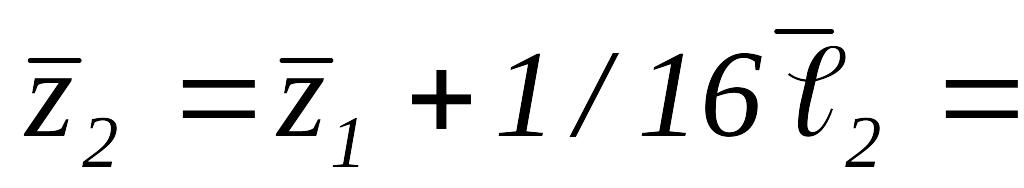
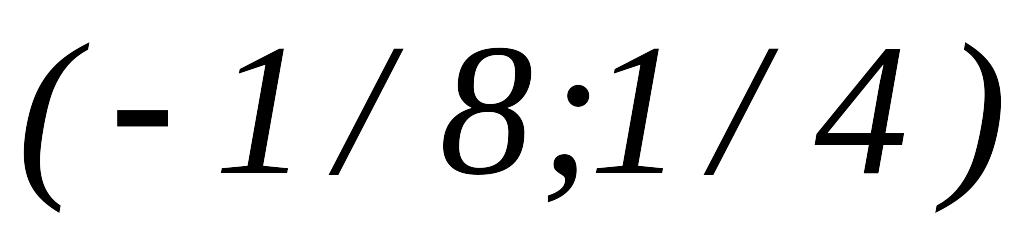 ,
,
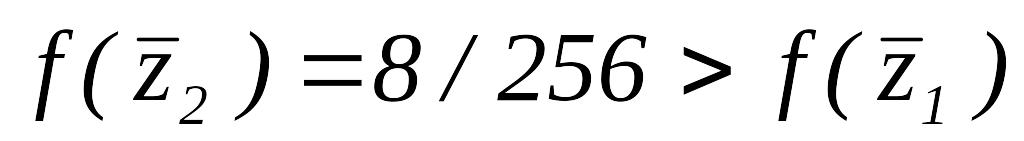 ,
тогда
,
тогда
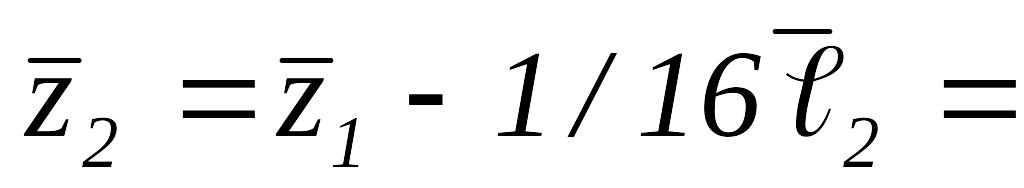
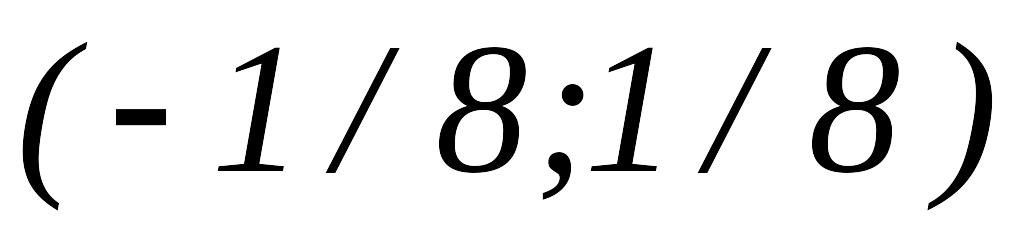 ,
,
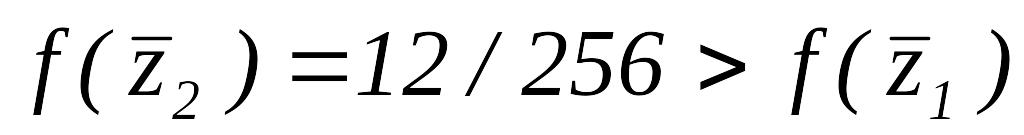 ,
то есть
,
то есть
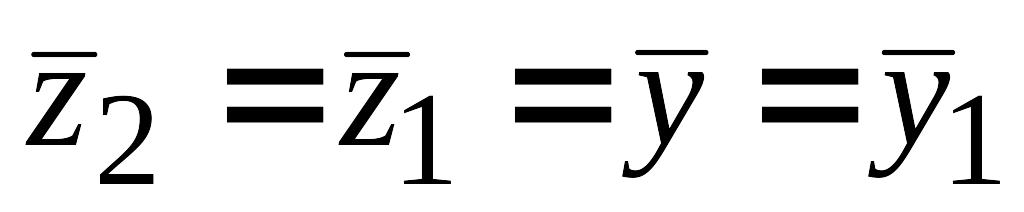 .
.Так как
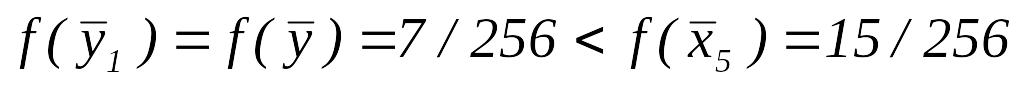 ,
то
,
то
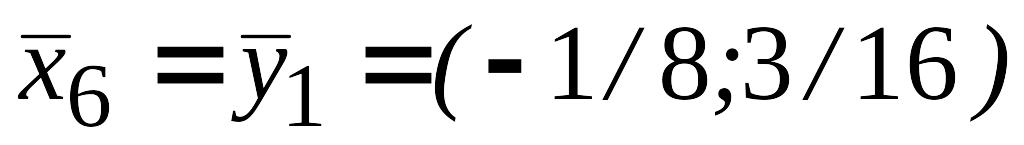 ,
,
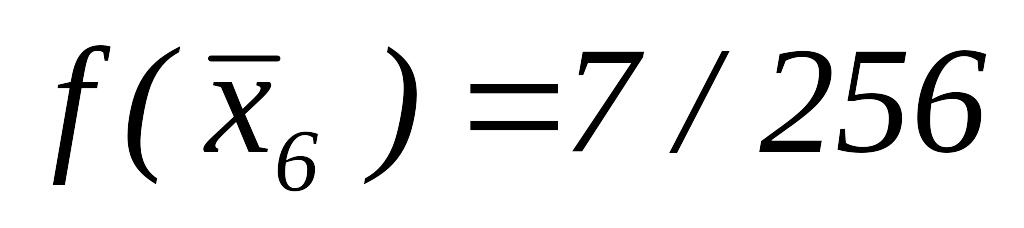 ,
полагаем
,
полагаем
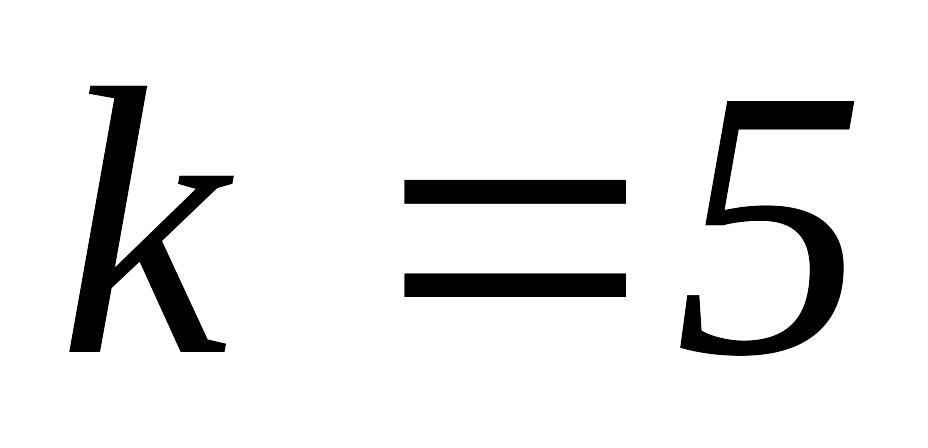 ,
переходим к шагу 4.
,
переходим к шагу 4.
ПО.

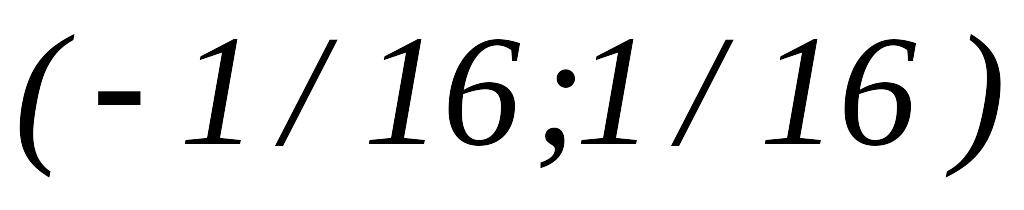 ,
,
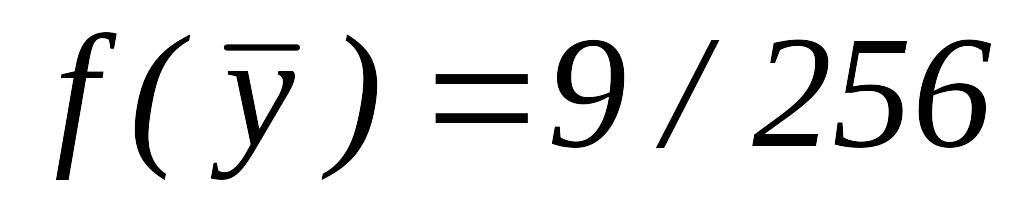 .
.ИП вокруг
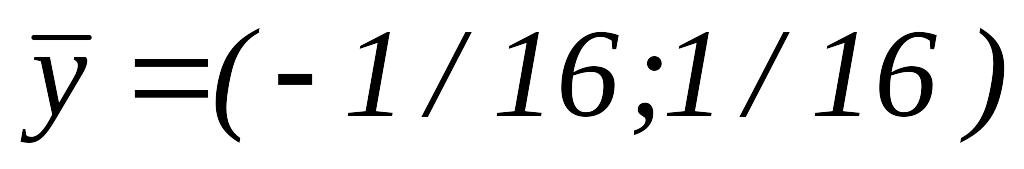 ,
.
Вычисляем
,
.
Вычисляем
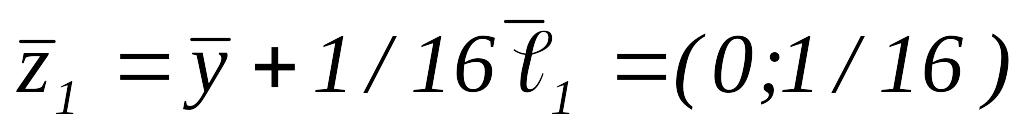 ,
,
,
,
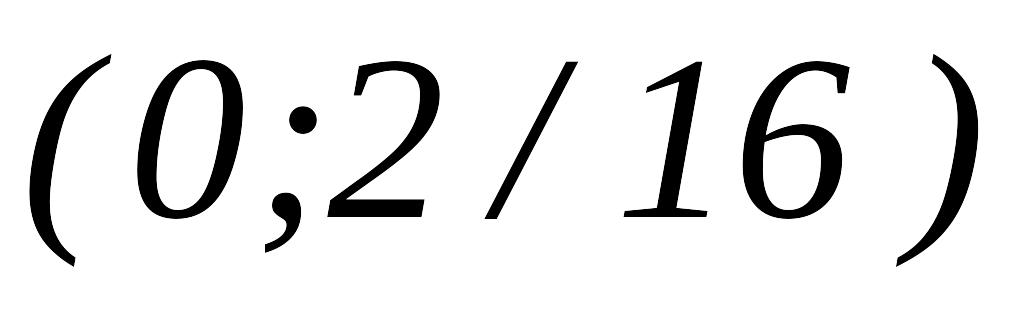 ,
,
тогда
,
,
тогда
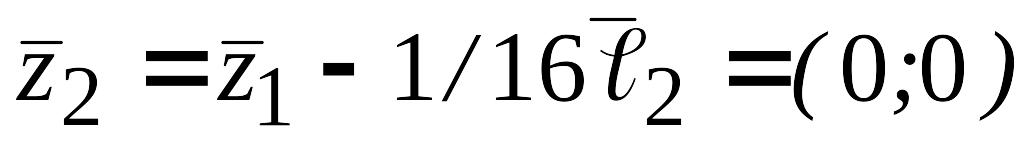 ,
,
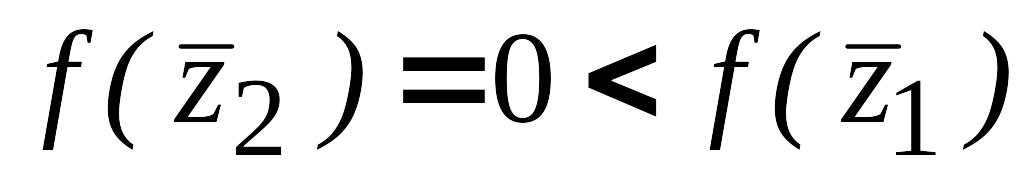 ,
т. е.
,
т. е.
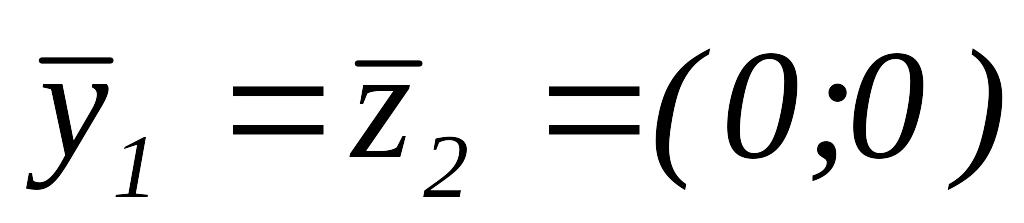 ,
,
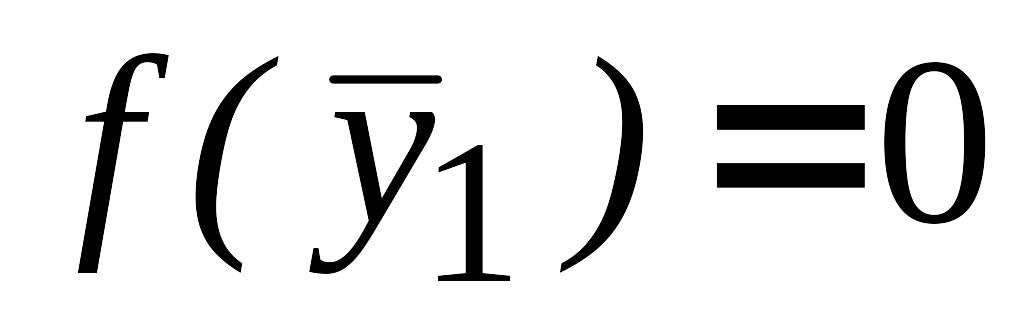 .
.Так как
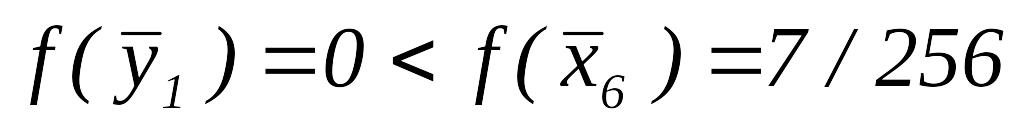 ,
положим
,
положим
 ,
положим
,
положим
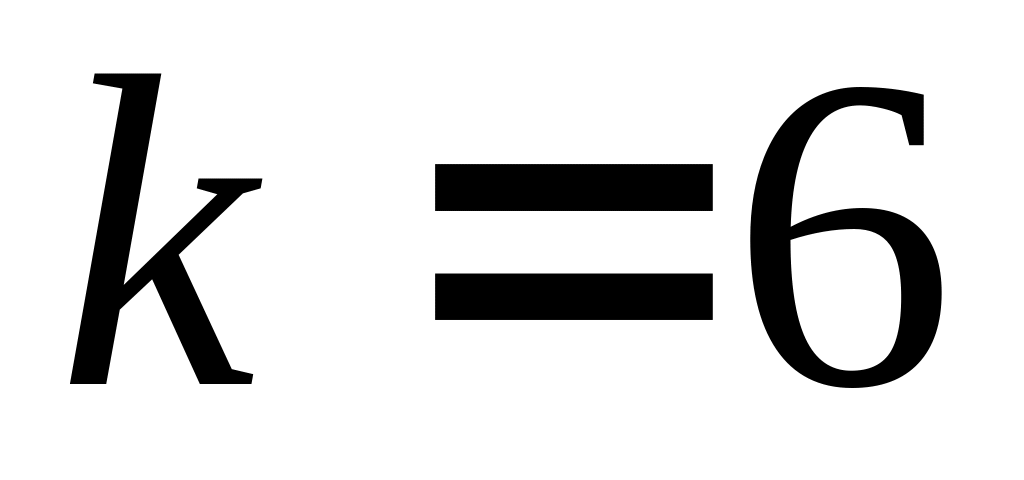 и перейдем к шагу 4.
и перейдем к шагу 4.
ПО.
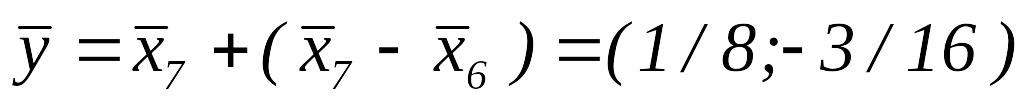 .
.ИП вокруг
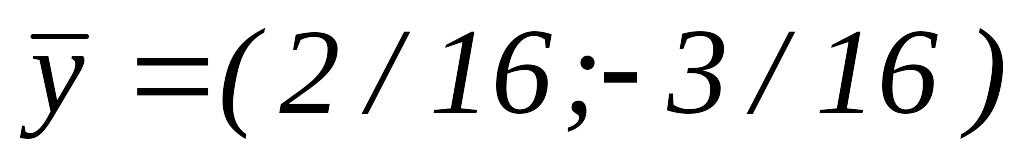 ,
.
,
.
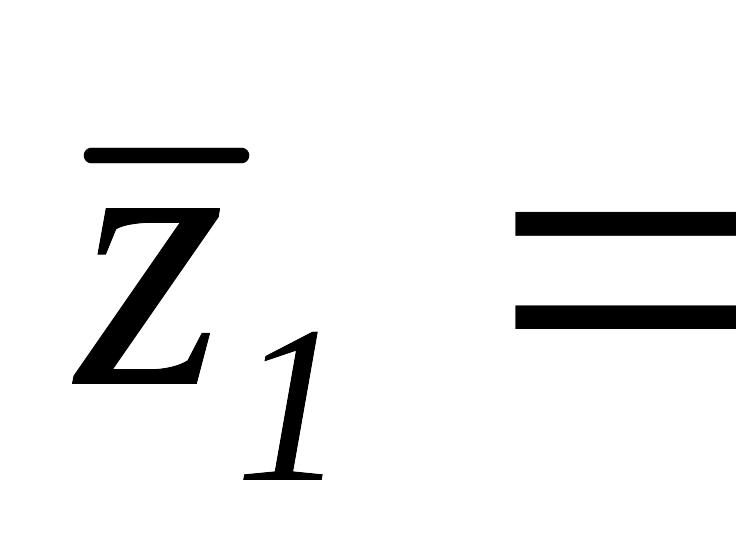
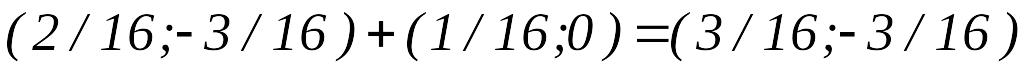 ,
,
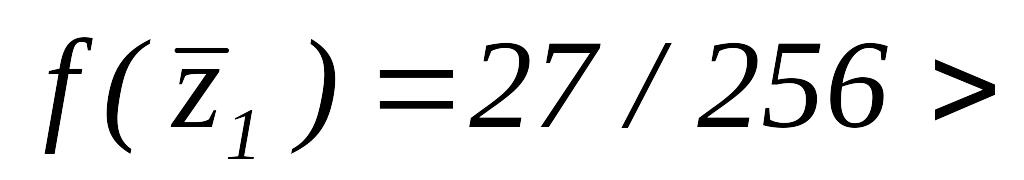 .
.
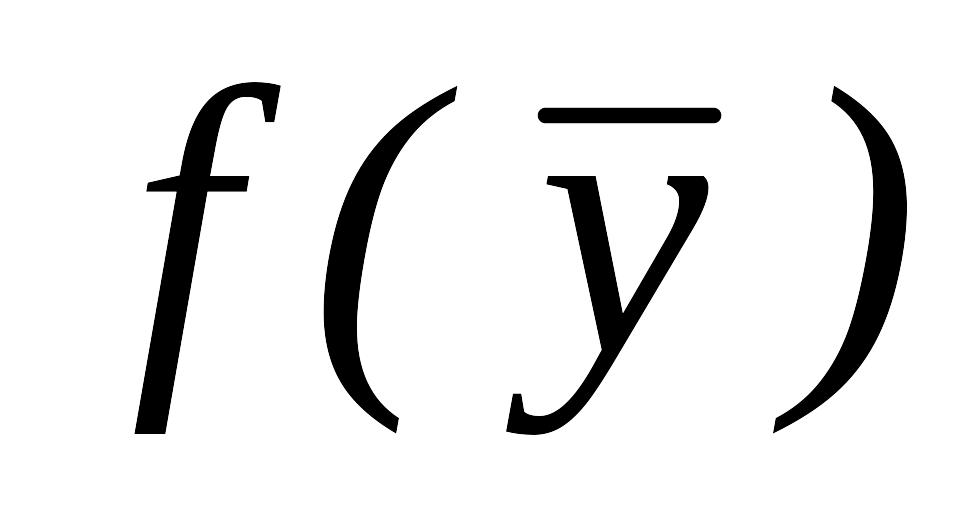 ,
,
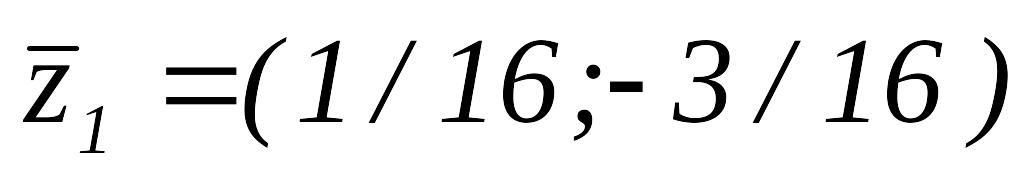 ,
,
,
,
,
,
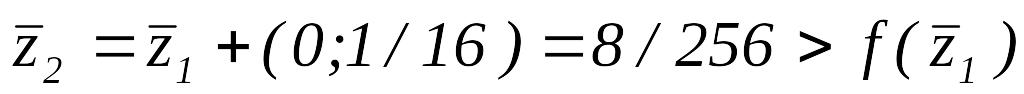 .
Таким образом,
.
Таким образом,
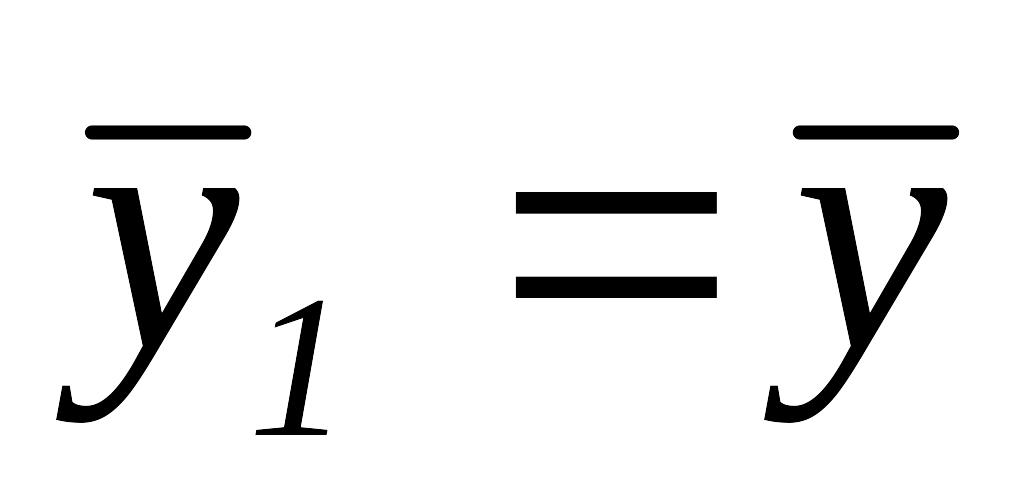 .
.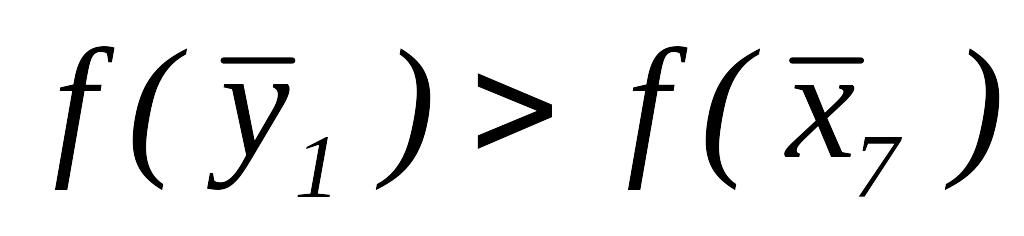 ,
переходим к шагу 3, полагая
,
переходим к шагу 3, полагая
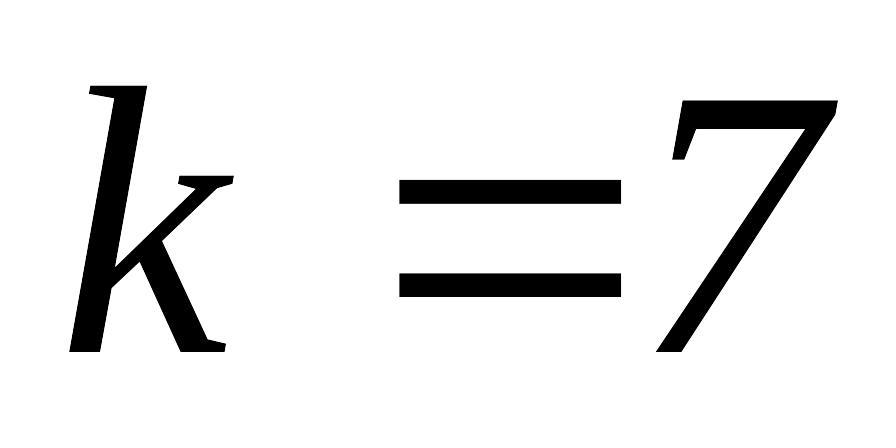 .
.
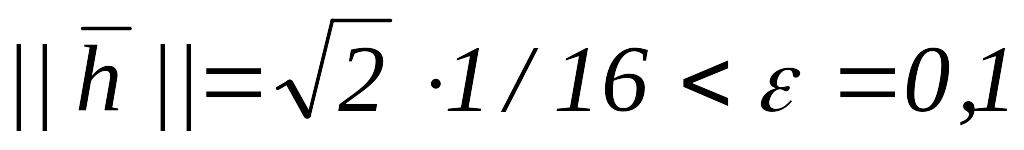 ,
следовательно,
,
следовательно,
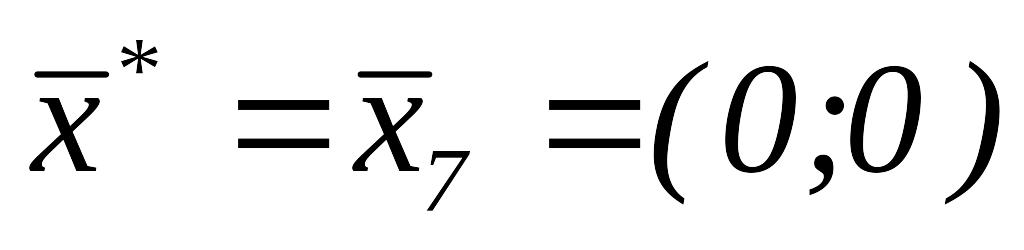 ,
.
,
.
Последовательные шаги алгоритма показаны на рис. 12.3.
Р.Хук и Т.Дживс предложили алгоритм, не содержащий одномерной оптимизации ни при ИП вдоль координатных направлений, ни при ПО. Очевидно, что можно рассматривать вариант метода Хука-Дживса с использованием методов одномерной оптимизации как на этапе ИП, так и при поиске по образцу.