
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
13.2. Методы возможных направлений
В этом параграфе рассматриваются методы, основанные на движении из одной допустимой точки в задаче (13.1) – (13.2) к другой допустимой точке с лучшим значением целевой функции. Имеется большое число методов возможных направлений; их теория была обоснована Зойтендейком. Вначале обсудим один вариант этих методов.
Основной алгоритм
Начальный этап. Задать и начальную точку .
Основной этап. ( -я итерация)
Шаг
1. Вычислить
![]() ,
,
![]() ,
,
![]() .
.
Шаг 2. Сформировать множество индексов
![]() .
.
Шаг
3. Проверить условие
![]() .
Если оно выполняется, то перейти к шагу
5, если нет – к шагу 4.
.
Если оно выполняется, то перейти к шагу
5, если нет – к шагу 4.
Шаг 4. Найти возможное направление подъёма функции в точке , решив следующую задачу линейного программирования:
![]() (13.4)
(13.4)
при ограничениях
![]() ,
,
![]() (13.5)
(13.5)
![]() (13.6)
(13.6)
![]() (13.7)
(13.7)
Решением
задачи (13.4) – (13.7) является вектор
![]() .
Перейти к шагу 6.
.
Перейти к шагу 6.
Шаг
5. Положить
,
![]() .
.
Шаг
6. Проверить условие
![]() .
Если оно выполняется, то положить
-
решение задачи. Если нет – перейти к
шагу 7.
.
Если оно выполняется, то положить
-
решение задачи. Если нет – перейти к
шагу 7.
Шаг
7. Решить одномерную оптимизационную
задачу, т. е. найти
в направлении
![]() .
Решение состоит из двух этапов:
.
Решение состоит из двух этапов:
1) найти
положительные корни уравнений
![]() ,
.
Выделим из всех
,
.
Выделим из всех
![]() :
:
![]() ,
,
![]() ;
;
2) найти
![]() ,
,
![]() .
.
Получаем .
Шаг 8. и перейти к шагу 1.
На
шаге 3 проверяется, является точка
внутренней точкой или граничной точкой
области
.
Если
-
внутренняя точка области
,
то в качестве направления
берётся
![]() -
направление скорейшего подъёма функции
в окрестности точки
.
Если же
-
направление скорейшего подъёма функции
в окрестности точки
.
Если же
![]() ,
то
лежит на границе области
и на шаге 4 ищется возможное направление
подъёма функции
в точке
(в результате решения ЗЛП).
,
то
лежит на границе области
и на шаге 4 ищется возможное направление
подъёма функции
в точке
(в результате решения ЗЛП).
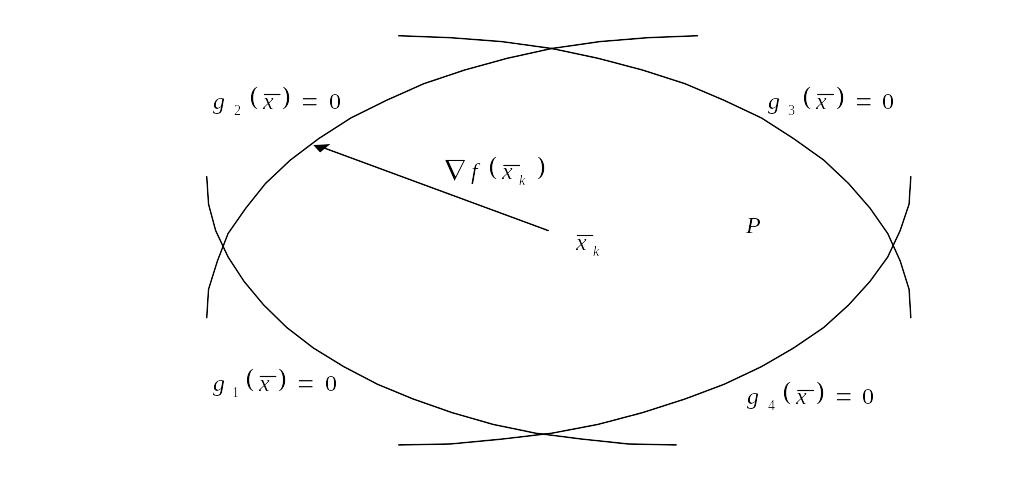
Рисунок 13.3
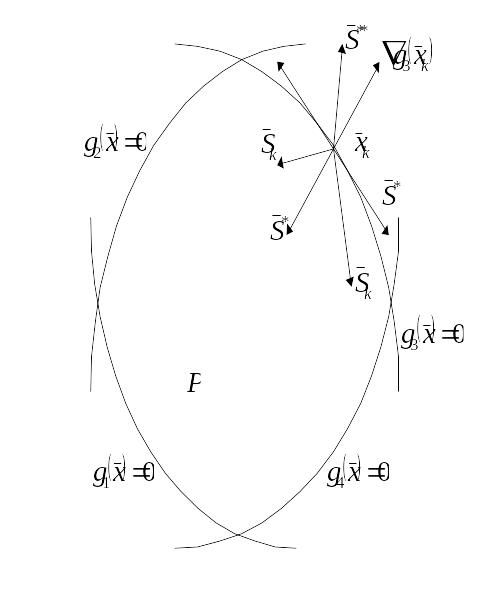
Рисунок 13.4
На
рис. 13.3 и 13.4 показаны направления
скорейшего подъёма, если
-
внутренняя точка области
(рис. 13.3), и множество возможных направлений
в точке
,
если
-
граничная точка области
(рис. 13.4). Здесь
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Сформулируем теперь необходимые и достаточные условия возможного направления в граничной точке области .
Теорема 13.1. Для того чтобы направление было возможным в граничной точке множества . Необходимо
![]() ,
, (13.8)
и
достаточно
,
, (13.8)
и
достаточно
![]() ,
. (13.9)
,
. (13.9)
Таким образом, чтобы найти возможное направление в граничной точке множества , достаточно найти вектор , удовлетворяющий неравенствам (13.9) (см. рис. 13.4).
Для граничной точки области введём в рассмотрение множество
![]() .
.
Очевидно,
что если
![]() хотя бы при одном
хотя бы при одном
![]() ,
то
,
,
то
,
![]() и, следовательно,
-
возможное направление в граничной точке
.
и, следовательно,
-
возможное направление в граничной точке
.
Осталось решить вопрос, как выбрать возможное направление подъёма функции в граничной точке области .
Теорема 13.2. Если в граничной точке
, , и
![]() ,то
вектор
есть возможное направление подъёма
функции
в точке
.
,то
вектор
есть возможное направление подъёма
функции
в точке
.
Возможное направление подъёма функции в граничной точке области можно найти, решая следующую задачу линейного программирования (см. шаг 4 алгоритма):
(13.10) при условиях:
, , (13.11)
![]() ,
(13.12)
,
(13.12)
![]() ,
.
(13.13)
,
.
(13.13)
В
самом деле, если вектор
![]() -
решение ЗЛП (13.10) – (13.13) и
-
решение ЗЛП (13.10) – (13.13) и
![]() ,
то по теореме 13.2
-
возможное направление подъёма функции
в точке
области
,
так как в этом случае
,
то по теореме 13.2
-
возможное направление подъёма функции
в точке
области
,
так как в этом случае
,
![]() .
.
Важно отметить, что ЗЛП (13.10) – (13.13) всегда разрешима, т. е. всегда можно указать возможные направления подъёма функции в точке .
В заключение отметим, что метод возможных направлений является обобщением метода скорейшего подъёма решения задачи безусловной оптимизации на задачу условной оптимизации.
Пример
13.1.
![]()
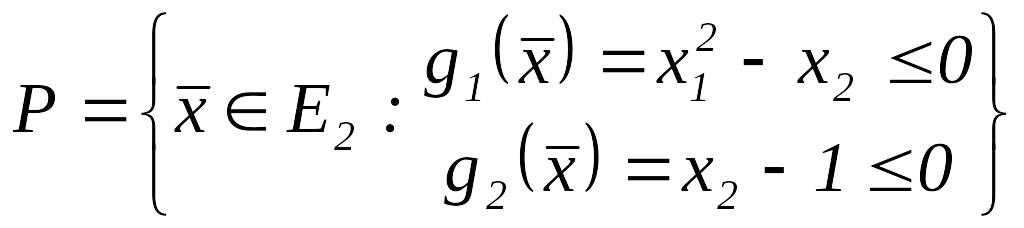
Решим эту задачу методом возможных направлений, сформулировав её в каноническом виде:
![]()
![]()
![]()
Начальный этап. Выберем в качестве начальной точку
![]()
Основной этап.
Итерация 1.
Вычисляем
вектор-градиент в точке
![]() :
:
![]() ,
,
![]() .
.
Вычисляем
![]() (точка на границе),
(точка на границе),
![]() (точка на границе).
(точка на границе).
Тогда
![]() ;
;
![]() .
.
Сформируем
множество
![]() :
:
![]() .
.
![]() ,
следовательно, для нахождения возможного
направления подъёма
,
следовательно, для нахождения возможного
направления подъёма
![]() функции
в точке
,
лежащей на границах
функции
в точке
,
лежащей на границах
![]() и
и
![]() области
,
сформулируем ЗЛП:
области
,
сформулируем ЗЛП:
![]()
![]()
![]()
![]()
или в каноническом виде:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решаем эту ЗЛП симплексным методом:
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
6 |
0 |
0 |
-2 |
2 |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
1 |
-1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
1 |
-1 |
1 |
-1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
9 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
10 |
0 |
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
11 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
12 |
0 |
1 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
-1 |
|
|
|
|
|
|
|
|
1 |
5 |
1 |
0 |
-2 |
2 |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
2 |
-2 |
2 |
-2 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
3 |
-3 |
2 |
-2 |
0 |
-1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
9 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
10 |
0 |
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
11 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
12 |
0 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
-2 |
2 |
-1 |
1 |
- |
1 |
|
|
|
|
|
|
|
2 |
5 |
1 |
0 |
0 |
0 |
1/3 |
-1/3 |
1 |
1/3 |
0 |
2/3 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
2/3 |
-2/3 |
0 |
-1/3 |
1 |
-2/3 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
-1 |
2/3 |
-2/3 |
0 |
-1/3 |
0 |
1/3 |
1 |
0 |
0 |
0 |
|
9 |
0 |
1 |
0 |
0 |
2/3 |
2/3 |
0 |
1/3 |
0 |
-1/3 |
1 |
0 |
0 |
0 |
|
10 |
0 |
1 |
0 |
0 |
2/3 |
-2/3 |
0 |
-1/3 |
0 |
-1/3 |
0 |
1 |
0 |
0 |
|
11 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
12 |
0 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
- |
0 |
1/3 |
-1/3 |
- |
1/3 |
- |
2/3 |
- |
- |
- |
- |
|
3 |
5 |
1 |
1/3 |
0 |
0 |
0 |
0 |
1 |
1/3 |
0 |
2/3 |
0 |
0 |
0 |
1/3 |
7 |
0 |
2/3 |
0 |
0 |
0 |
0 |
0 |
-1/3 |
1 |
-2/3 |
0 |
0 |
0 |
2/3 |
|
1 |
0 |
2/3 |
1 |
-1 |
0 |
0 |
0 |
-1/3 |
0 |
1/3 |
0 |
0 |
0 |
2/3 |
|
9 |
0 |
1/3 |
0 |
0 |
0 |
0 |
0 |
1/3 |
0 |
-1/3 |
1 |
0 |
0 |
-2/3 |
|
10 |
0 |
5/3 |
0 |
0 |
0 |
0 |
0 |
-1/3 |
0 |
1/3 |
0 |
1 |
0 |
2/3 |
|
11 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
5/3 |
- |
0 |
0 |
- |
- |
1/3 |
- |
- |
- |
- |
- |
2/3 |
|
Итак,
![]() ,
,
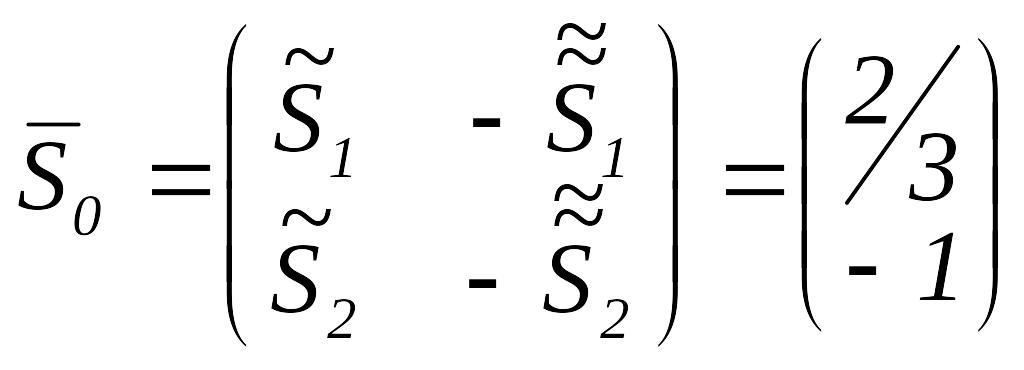 ,
,
![]() ,
следовательно,
,
следовательно,
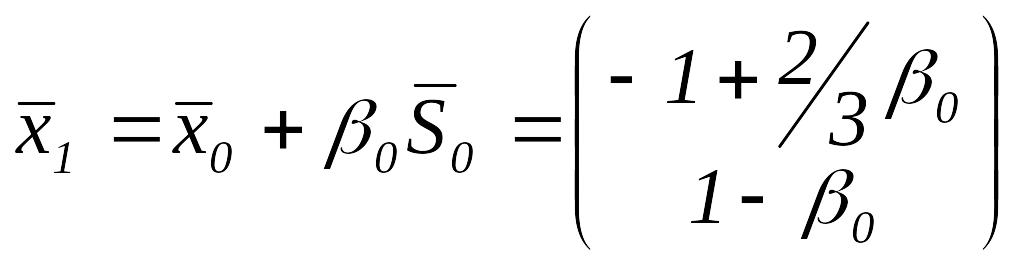 .
.
Вычисляем
значение
![]() :
:
![]()
![]()
![]() ;
;
![]() ;
;
![]() .
.
Решим теперь одномерную задачу
![]()
![]() или
или
![]()
![]() .
.
Получаем
![]() .
Отсюда
.
Отсюда
![]() .
.
Итерация 2.
Вычисляем
![]() ,
,
![]() :
:
![]() ,
,
![]() .
.
Тогда
![]() .
.
Сформируем
множество
![]()
![]() .
.
![]() ,
следовательно, для нахождения возможного
направления подъёма
функции
в точке
,
лежащей на границе
области
,
сформулируем вновь ЗЛП:
,
следовательно, для нахождения возможного
направления подъёма
функции
в точке
,
лежащей на границе
области
,
сформулируем вновь ЗЛП:
![]()
или в каноническом виде:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Решаем задачу симплексным методом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
6 |
0 |
0 |
-1 |
1 |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
1 |
-1 |
1 |
-1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
8 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
9 |
0 |
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
10 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
11 |
0 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
-1 |
- |
- |
- |
- |
- |
- |
|
1 |
5 |
1 |
0 |
-1 |
1 |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
2 |
-2 |
2 |
-2 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
|
8 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
9 |
0 |
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
10 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
11 |
0 |
1 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
-1 |
1 |
-1 |
1 |
- |
1 |
- |
- |
- |
- |
- |
|
2 |
5 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1/ 2 |
1/ 2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
-1 |
1 |
-1 |
0 |
-1/ 2 |
1/ 2 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
0 |
0 |
-1 |
1 |
0 |
1 /2 |
-1/ 2 |
1 |
0 |
0 |
0 |
|
9 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
-1/2 |
1/ 2 |
0 |
1 |
0 |
0 |
|
10 |
0 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
11 |
0 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
- |
0 |
0 |
0 |
- |
1/2 |
1/2 |
- |
- |
- |
- |
|
Итак,
![]() ,
следовательно,
,
следовательно,
![]() .
.
Ответ:
![]() ,
,
![]() .
.
Решение задачи проиллюстрировано рис.3.5
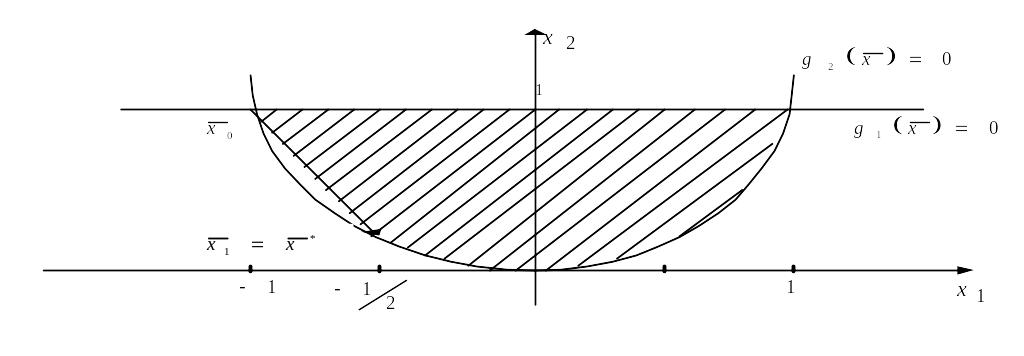
Шаг 3.Рисунок 13.5
