Глава 13. Методы условной оптимизации

13.1. Постановка задачи. Классификация методов

В дальнейшем будем рассматривать следующую задачу:

(13.1)

на множестве :

, (13.2)

где и - нелинейные функции.

При решении задач нелинейного программирования ввиду нелинейности функций выпуклость допустимого множества решений и конечность числа его крайних точек (в отличие от ЗЛП) необязательны. Задача нелинейного программирования не всегда имеет решение. Если задача имеет решение, то максимум функции может достигаться в крайней точке допустимой области значений , в одной из граничных точек или в точке, расположенной внутри допустимой области .

Определение 13.1. Решением или точкой максимума задачи условной оптимизации будем называть такой вектор , что для всех , т. е. .

Определение 13.2. Будем называть направление возможным в точке , если существует такое действительное число , что для всех .

Определение 13.3. Вектор будем называть возможным направлением подъёма функции в точке , если существует такое действительное число , что для всех :

и .

Методы решения задачи условной оптимизации можно представить как итеративный процесс, в котором, исходя из начальной точки , получают последовательность точек , монотонно увеличивающих значения функции . Это так называемые методы подъёма. Элементы этой последовательности точек определяются следующим образом: , где - возможное направление подъёма функции в точке , находятся при решении задачи одномерной оптимизации: . Если точка - внутренняя точка множества , т. е. для : , то всякое направление в ней является возможным (пример на рис. 13.1).

Если точка - граничная точка области , то возможные направления определяются ограничениями (направление на рис 13.2 возможным не является).

Прежде чем определять направление подъёма функции в точке , следует вычислить множество таких возможных направлений , для которых существовала бы окрестность точки , принадлежащая .

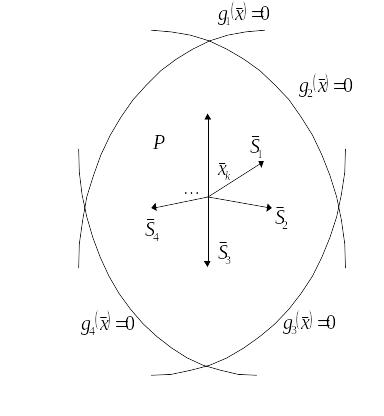
Рисунок 13.1

Рисунок 13.2

Общая схема методов условной оптимизации

Начальный этап. Задать и выбрать начальную точку .

Основной этап.

Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.

Шаг 2. Положить , где находим, решая задачу , .

Шаг 3. Заменить на и перейти к шагу 1.

Конкретные методы условной оптимизации различаются способом выбора возможного направления подъёма функции в точке .

Вообще говоря, методы решения задач нелинейного программирования с ограничениями можно разбить на следующие классы.

1. Методы, которые непосредственно применяются к задаче (13.1) – (13.2). Сюда можно отнести, например, такие методы, на которые можно смотреть как на естественные обобщения изложенных во второй главе пособия градиентных методов.

2. Методы, основанные на решении последовательности вспомогательных задач, которые могут быть, к примеру, задачами линейного программирования, возникающими путём замены целевой функции и функций ограничений задачи (13.1) – (13.2) на линейные или кусочно-линейные.

Для первого класса методов соотношение

, , (13.3)

которое при лежит в основе градиентных методов, не будет пригодным при определении решения задачи (13.1) – (13.2), поскольку для граничной точки множества , не являющейся решением задачи (3.1) – (13.2), и для , вообще говоря, не существует числа такого, что . Поэтому соотношение (13.3) различными способами модифицируется в методах проекций и методах возможных направлений.

Методы проекций основаны на построении проекции на множество : .

Методы проекций сходятся со скоростью геометрической проекции.

Методы возможных направлений основаны на следующем: при движении из точки в соответствии с (13.3) вектор и число выбираются таким образом, чтобы точка была допустимой и . Среди методов возможных направлений можно выделить методы Зойтендейка, проектируемых градиентов, приведённых градиентов. Методы возможных направлений имеют линейную скорость сходимости. Они используют производные целевой функции и функций ограничений первого порядка. В настоящее время для достижения более высокой скорости сходимости разработаны также методы возможных направлений, применяющие производные второго порядка.

Отметим теперь некоторые методы из второго класса.

В основе метода штрафных функций лежит идея введения “штрафа” за нарушение ограничений задачи (13.1) – (13.2). Для этого вместо этой задачи решается последовательность вспомогательных задач без ограничений:

,

где при , - штрафные функции.

Если в методе штрафных функций каждая не оптимальная в задаче (13.1) – (13.2) интервальная точка не является допустимой и для этой задачи, то в методе барьеров, наоборот, все итерационные точки допустимы. Вспомогательные задачи при этом составляются так, чтобы целевые функции задачи (13.1) – (13.2) и вспомогательных задач не отличались значительно внутри допустимой области , но при прибли­жении к границе происходило сильное изменение целевой функции вспомогательной задачи. Такого рода "барьеры" обеспечивают принад­лежность решения вспомогательных задач внутренности допустимой об­ласти, и с такими задачами можно обращаться как с задачами без огра­ничений.

Помимо названных существует также целый ряд методов решения задач условной оптимизации, которые ориентированы на различные ти­пы задач. По типу решаемых задач методы условной оптимизации можно разделить на два основных класса:

1. Методы решения задач с линейными ограничениями;

2. Meтоды решения задач с нелинейными ограничениями (как равенст­вами, так и неравенствами).

В настоящем учебном пособий рассмотрены некоторые методы из перечисленных выше классов.