
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
Методы первого и второго порядков
Методы нулевого порядка, рассмотренные в предыдущем разделе используют только значения целевой функции . Необходимость методов прямого поиска несомненна, особенно при решении практических задач. Но, с другой стороны, при использовании даже очень эффективных прямых методов иногда требуется большое количество вычислений значений функции, что может привести либо к переполнению памяти ЭВМ, либо к чрезмерным затратам времени. Поэтому необходимо рассмотрение методов, основанных на использовании первых и вторых производных функции .
Градиентные методы. Метод скорейшего спуска – метод Коши
Градиентные методы основаны на линейной аппроксимации целевой функции в окрестности точки , в которой требуется определить направление наискорейшего локального спуска, т.е. наибольшего локального уменьшения значения функции. Для определения этого направления разложим функцию в окрестности точки в ряд Тейлора:
![]() (12.3)
(12.3)
и отбросим член второго порядка и выше.
Наибольшее
уменьшение значения функции
будет достигнуто при выборе такого
направления
,
которое минимизирует скалярное
произведение
![]() .
Из свойств скалярного произведения
следует, что данное произведение примет
минимальное значение при
.
Из свойств скалярного произведения
следует, что данное произведение примет
минимальное значение при
![]() .
.
Методы безусловной оптимизации, в которых в качестве направления поиска берется градиент функции , называются градиентными. Градиентные методы являются методами первого порядка. Таким образом, последовательность точек генерируется градиентным методом в соответствии с формулой
![]() , (12.4)
, (12.4)
где
– параметр, характеризующий величину
шага вдоль направления. Величина шага
может выбираться разными способами.
Если значение параметра
![]() вычисляется путем решения задачи
одномерной оптимизации, то градиентный
метод называется методом скорейшего
спуска, или методом Коши.
вычисляется путем решения задачи
одномерной оптимизации, то градиентный
метод называется методом скорейшего
спуска, или методом Коши.
Алгоритм метода Коши
Начальный этап. Выбрать – начальную точку и – параметр окончания счета, положить .
Основной этап.
Если
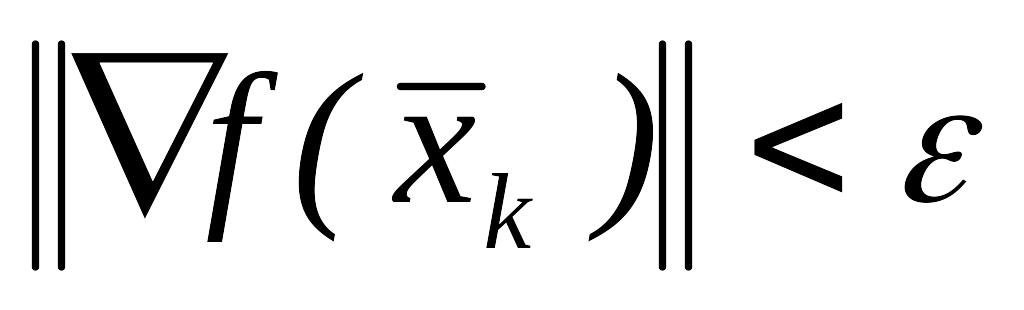 ,
то
,
остановится.
,
то
,
остановится.Положить
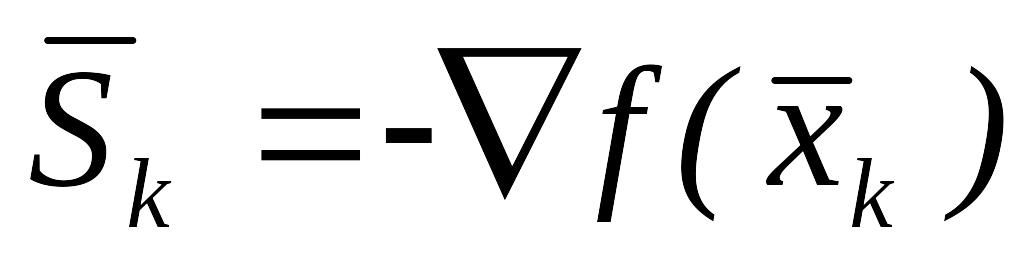 ,
вычислить
,
вычислить
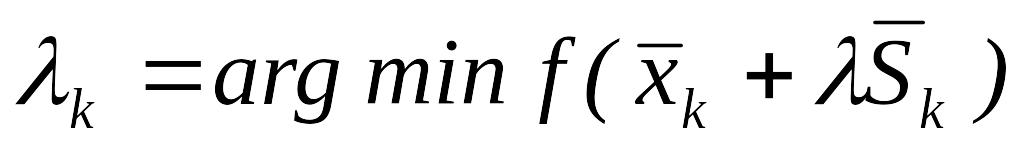 ,
,
положить
и перейти к шагу 1.
,
,
положить
и перейти к шагу 1.
Пример 12.5. Найти минимум функции методом Коши:
![]() .
.
Начальный
этап. Пусть
![]() ,
,
,
,
,
,
![]() .
.
Основной этап.
Вычислим
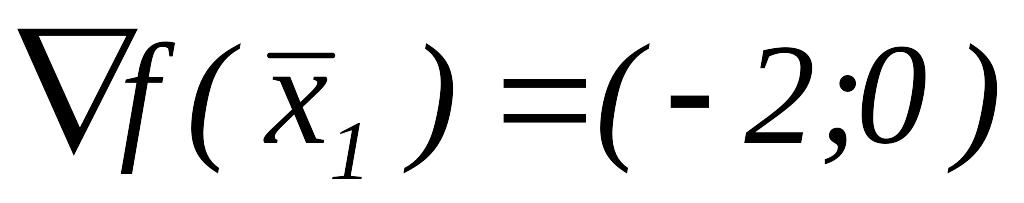 ,
так как
,
так как
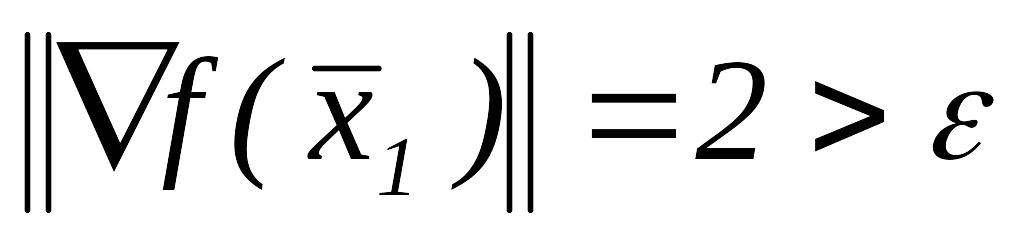 ,
переходим к шагу 2.
,
переходим к шагу 2.Положить
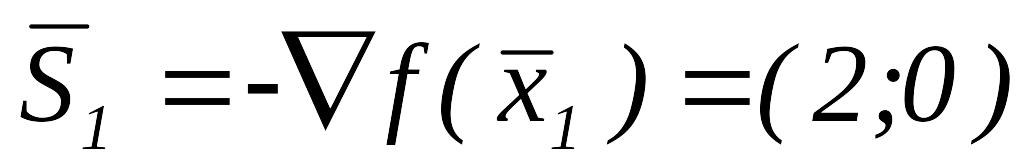 ,
вычислить
,
вычислить
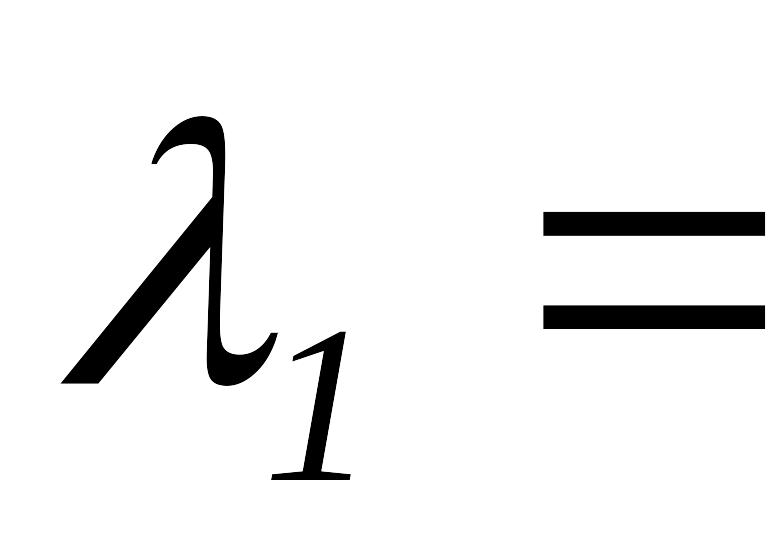
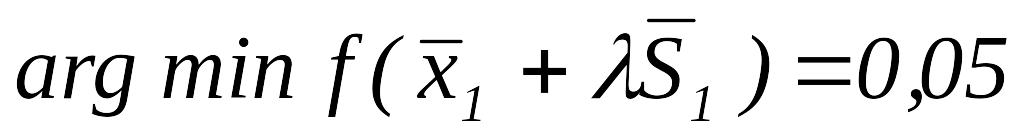 ,
,
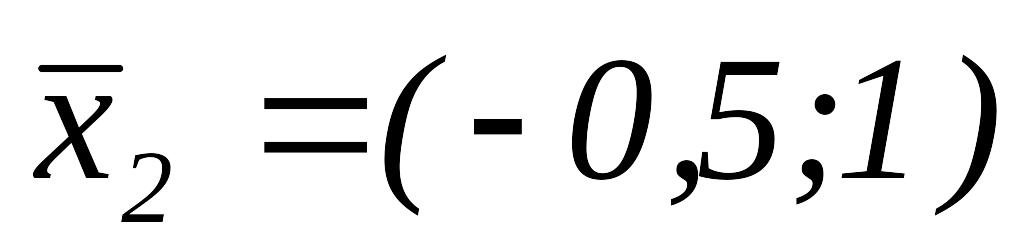 ,
положить
,
положить
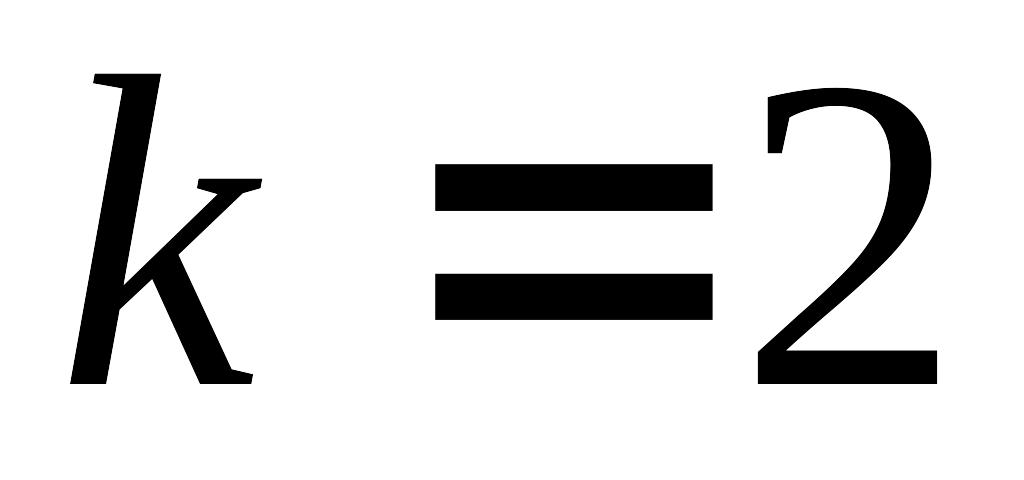 и перейти к шагу 1.
и перейти к шагу 1.Вычислим
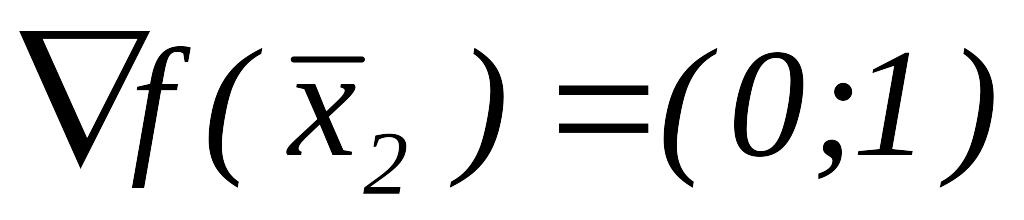 ,
так как
,
так как
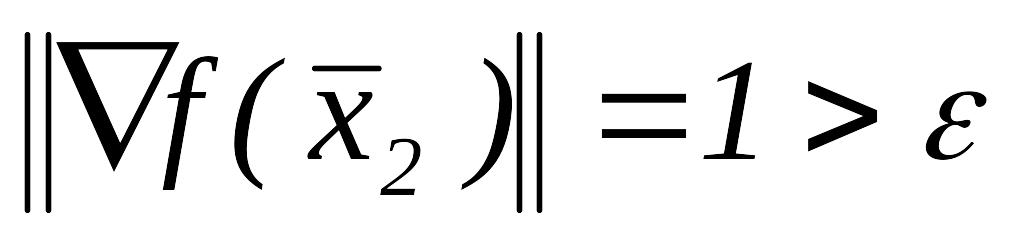 ,
переходим к шагу 2.
,
переходим к шагу 2.Положить
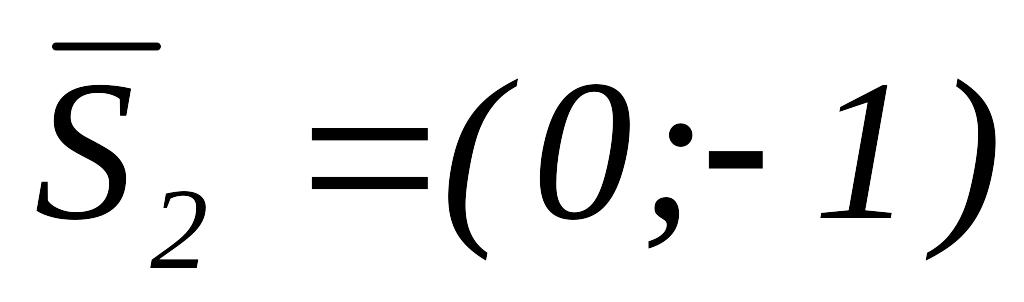 ,
вычислить
,
вычислить
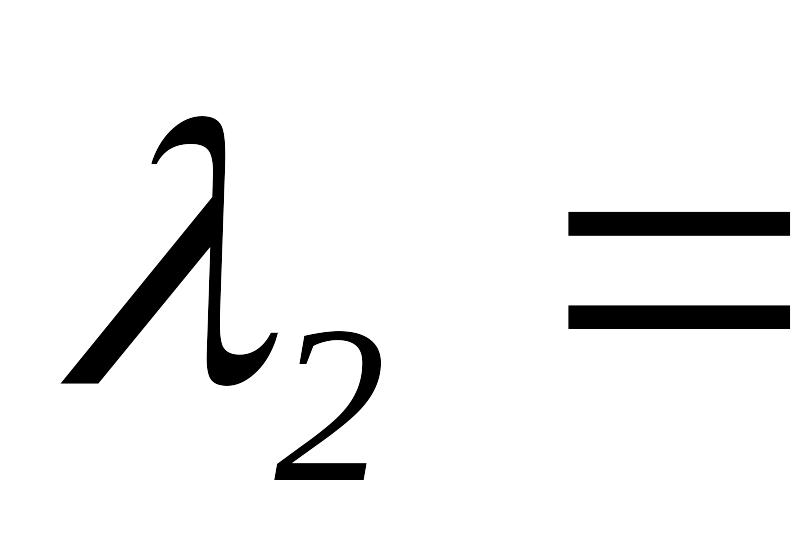
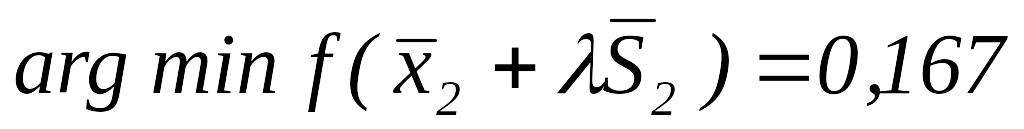 ,
,
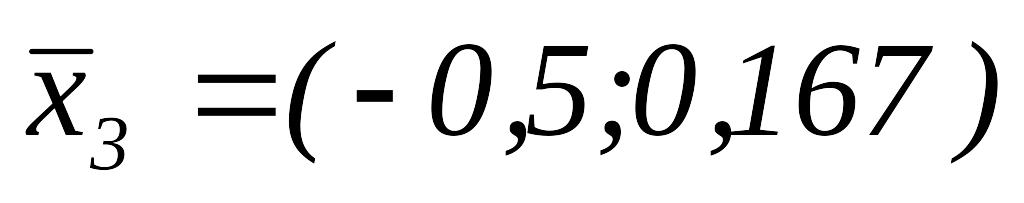 ,
положить
и перейти к шагу 1.
,
положить
и перейти к шагу 1.
Результаты
вычислений приведены в табл. 12.3 и на
рис. 12.7. Из таблицы следует, что значение
функции
становится меньше
![]() на 11-й итерации, а значение нормы градиента
станет меньше
на 11-й итерации, а значение нормы градиента
станет меньше
![]() только при
только при
![]() ,
так как значение нормы градиента
уменьшается в 5/6 раза каждые две итерации
(см. табл. 12.3).
,
так как значение нормы градиента
уменьшается в 5/6 раза каждые две итерации
(см. табл. 12.3).
Таблица 12.3
k |
|
|
|
|
|
|
1 |
(- |
|
(-2; 0) |
2 |
0,05 |
(- |
2 |
(- ; 1) |
|
(0; 1) |
1 |
1/6 |
(- |
3 |
(- ; ) |
|
(- |
|
0,05 |
( |
4 |
( |
|
(0;
|
|
1/6 |
( |
5 |
( ) |
|
( |
|
0,05 |
( |
6 |
( ) |
|
(0;
|
|
1/6 |
( |
7 |
( ; ) |
|
( |
|
0,05 |
( |
|
…………… |
…….. |
………… |
……… |
…… |
…… |
11 |
( |
|
…….. |
|
|
|

Скорость
сходимости метода Коши (это видно из
примера 12.5) является довольно низкой,
хотя на каждой итерации обеспечивается
дополнение неравенства
![]() ,
причем метод позволяет, как правило,
существенно уменьшить значение функции
при движении из точек, расположенных
на значительном расстоянии от точки
минимума, т.е. на начальных шагах процесса,
когда второе слагаемое в формуле (12.3),
определяющее приращение функции,
достаточно велико. Однако вблизи
оптимальной (стационарной) точки метод
Коши часто работает плохо, потому что
шаги по направлению
делаются маленькими (уменьшающимися).
Это явление называется явлением
“зигзага”. Явление “зигзага” и плохую
сходимость метода Коши на последних
итерациях можно объяснить, если разложение
(2.3) для
записывать в виде
,
причем метод позволяет, как правило,
существенно уменьшить значение функции
при движении из точек, расположенных
на значительном расстоянии от точки
минимума, т.е. на начальных шагах процесса,
когда второе слагаемое в формуле (12.3),
определяющее приращение функции,
достаточно велико. Однако вблизи
оптимальной (стационарной) точки метод
Коши часто работает плохо, потому что
шаги по направлению
делаются маленькими (уменьшающимися).
Это явление называется явлением
“зигзага”. Явление “зигзага” и плохую
сходимость метода Коши на последних
итерациях можно объяснить, если разложение
(2.3) для
записывать в виде
![]()
![]() , (12.5)
, (12.5)
где
![]() при
при
![]() .
.
Очевидно,
если точка
близка к оптимальной точке, где
![]() ,
то слагаемое
,
то слагаемое
![]() ,
определяющее приращение функции,
является очень малым и сравнимым по
порядку малости с не учитываемым в
методе Коши третьим слагаемым. Именно
поэтому метод Коши становится неэффективным
вблизи оптимальной точки. Метод Коши
основан на линейной аппроксимации
функции
,
чтобы построить более эффективный
алгоритм. Нужно привлечь информацию о
вторых производных функции
.
,
определяющее приращение функции,
является очень малым и сравнимым по
порядку малости с не учитываемым в
методе Коши третьим слагаемым. Именно
поэтому метод Коши становится неэффективным
вблизи оптимальной точки. Метод Коши
основан на линейной аппроксимации
функции
,
чтобы построить более эффективный
алгоритм. Нужно привлечь информацию о
вторых производных функции
.
