10.3. Достаточные условия оптимальности

Теорема 10.3. Пусть – седловая точка функции Лагранжа. Тогда – решение задачи (10.4), (10.5) и .

Доказательство. Из условия (10.14) теоремы 10.1. имеем и , , откуда .

Из неравенства (10.13) имеем

(10.32)

для всех .

В частности (10.32) верно для всех . Но при , так как и , . Поэтому из (10.32) следует, что для всех , т.е. – решение задачи (10.4), (10.5).

Замечание. Теоремы 10.1. и 10.3. доказаны без использования выпуклости функций , и вогнутости функции , т.е. наличие седловой точки функции Лагранжа определяет оптимальность точки для общей задачи математического программирования. Обратное утверждение, что из оптимальности точки следует существование седловой точки функции Лагранжа, справедливо лишь для задачи выпуклого программирования и при наличии дополнительных ограничений на множестве .

Теоремы, в которых устанавливается существование седловой точки функции Лагранжа задачи (10.4), (10.5), обычно называют теоремами Куна-Таккера.

10.4. Условия регулярности выпуклого множества

Определение 10.3. Множество , определяемое условиями (10.2), называется регулярным, если для любого существует точка , такая что

(10.33)

Определение 10.4. (условие регулярности Слейтера).

Множество , определяемое условиями (10.2), называется регулярным по Слейтеру, если существует точка , такая что

(10.34)

для всех .

Теорема 10.4. Определения 10.3 и 10.4 регулярного множества эквивалентны.

Доказательство. Пусть выполнено условие (10.34), тогда, полагая для всех , получим условие (10.33).

Обратно, пусть выполнены условия (10.33). Выберем , , , .

Тогда из теоремы 2.6 следует, что . Из теоремы 9.3. следует, что , т.е. выполняется условие (10.34).

10.5. Теорема Куна-Таккера. Общий случай

Теорема 10.5. Если в задаче выпуклого программирования (10.4)-(10.5) множество обладает свойством регулярности, то необходимым и достаточным условием оптимальности точки является существование такого , что точка является седловой точкой функции Лагранжа на множестве , .

Доказательство.

Достаточность условий теоремы доказана в теореме 10.3.

Необходимость. В пространстве рассмотрим два множества:

, (10.35)

. (10.36)

1. Множества и не имеют общих точек. Действительно, пусть , тогда существует , такая, что , , . Если при этом , то , откуда , т.е. . Если , то найдется номер , такой что , откуда , т.е. снова . Таким образом, .

2. и – выпуклые множества. Покажем, например, что выпукло. Пусть , тогда существуют точки , , такие что , , , , . Выберем произвольное , и положим , . Из вогнутости и выпуклости имеем ,

, т.е. , , , , следовательно, . Аналогично доказывается выпуклость .

3. В силу теоремы об отделимости выпуклых множеств существует гиперплоскость , разделяющая и и и . Это значит, что

(10.37)

для всех , .

Очевидно, что точка , действительно, если , то , , т.е. . С другой стороны, так как , то .

Из той же теоремы следует, что , т.е. неравенство (10.37) можно переписать в виде , , . (10.38)

4. Возьмем точку . Подставляя ее в левое неравенство (10.38), получим , откуда (10.39)

Далее, взяв , , из левого неравенства (10.38) получим , т.е. , . (10.40)

Таким образом, , .

5. Возьмем точку , тогда точки , . Подставляя эти точки в (10.38), получим , ,

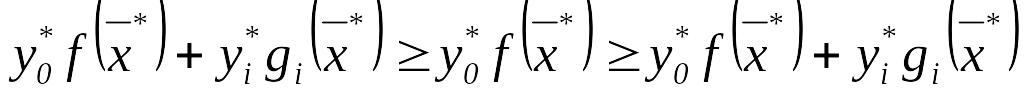откуда , . (10.41)

Таким образом, доказано выполнение равенств (10.14) из теоремы 10.1.

6. По условию регулярности существует точка , такая что для всех . Тогда точка , подставляя ее в (10.38), получим . (10.42)

Если допустить, что , и так как по предположению не все , , то из (10.42) получим (10.43)

Полученное противоречие показывает, что . Неравенство (10.38) поделим на , это значит, что в (10.38) можно принять .

7. Возьмем произвольную точку . Тогда . Подставляя эту точку в правое неравенство (10.38) и учитывая, что , получим . В силу (10.41) и из предыдущего неравенства имеем , т.е. условие (10.13) теоремы 10.1.. Таким образом, согласно теореме 10.1 – седловая точка.

Если в задаче выпуклого программирования (10.4), (10.5) функции и , являются непрерывно дифференцируемыми, то теоремы 10.2. и 10.5. можно объединить в одну (теорема 10.6).

Теорема 10.6. Если в задаче выпуклого программирования (10.4), (10.5) множество обладает свойствами регулярности, то необходимым и достаточным условием оптимальности точки является существование такого , что для точки выполняются условия (10.18)-(10.23).