8.2. Решение примеров.
Пример 8.1.
(1)
при условиях
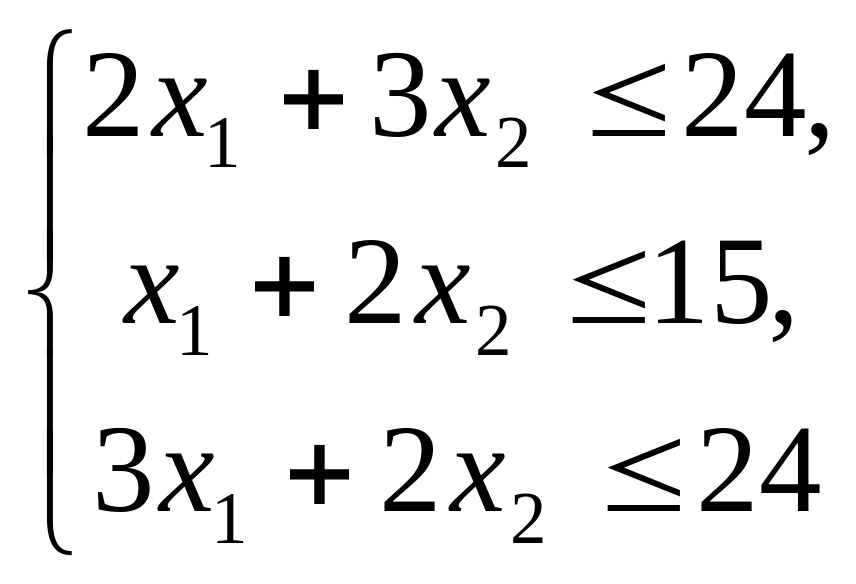(2)
(3)
Решение. Так как целевая функция (1) нелинейная, то задача (1) - (3)
является задачей нелинейного программирования. Областью допустимых
решений данной задачи является многоугольник OABC (рис. 8.1). Следовательно, для нахождения ее решения нужно определить такую
точку многоугольника OABC, в которой функция (1) принимает
максимальное значение. Построим линию уровня:
где
h
- некоторая
постоянная, и исследуем ее поведение
при различных значениях h.
При
каждом значении h
получаем
параболу, которая тем выше отдалена
от оси
,
чем
больше значение h
(рис.
8.1). Значит, функция F
принимает
максимальное значение в точке касания
одной из парабол с границей многоугольника
ОАВС.
В
данном случае это точка D
(рис.
8.1), в которой линия уровня:
касается стороны АВ многоугольника ОАВС. Координаты точки D можно найти из системы уравнений:
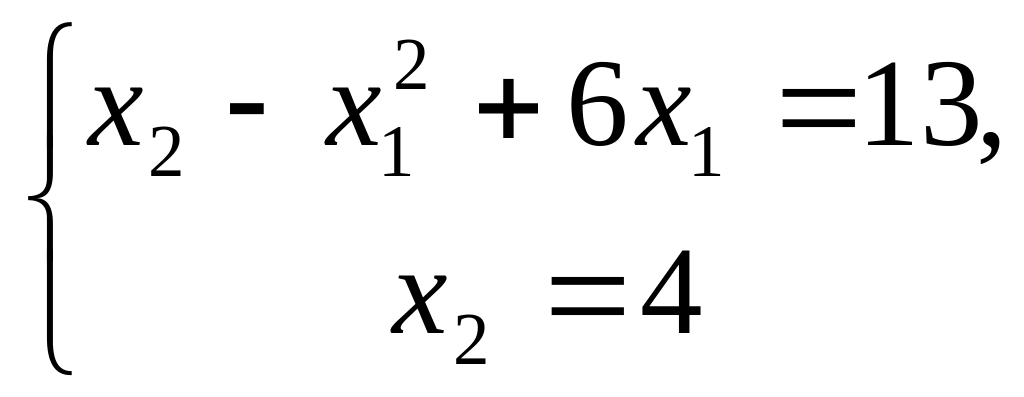
Решая
эту систему, получим
.
Итак
при
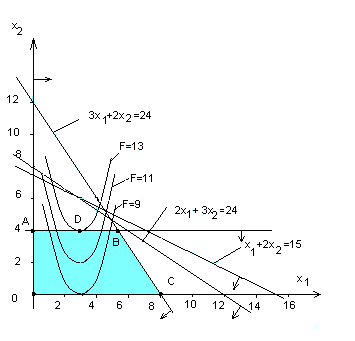
Рис. 8.1.
Как видим, в задаче (1) - (3) точка максимального значения целевой функции не является вершиной многоугольника решений. Поэтому процедура перебора вершин, которая использовалась при решении задач линейного программирования, неприменима для решения данной задачи.
Пример 8.2.
(5)
при условиях:
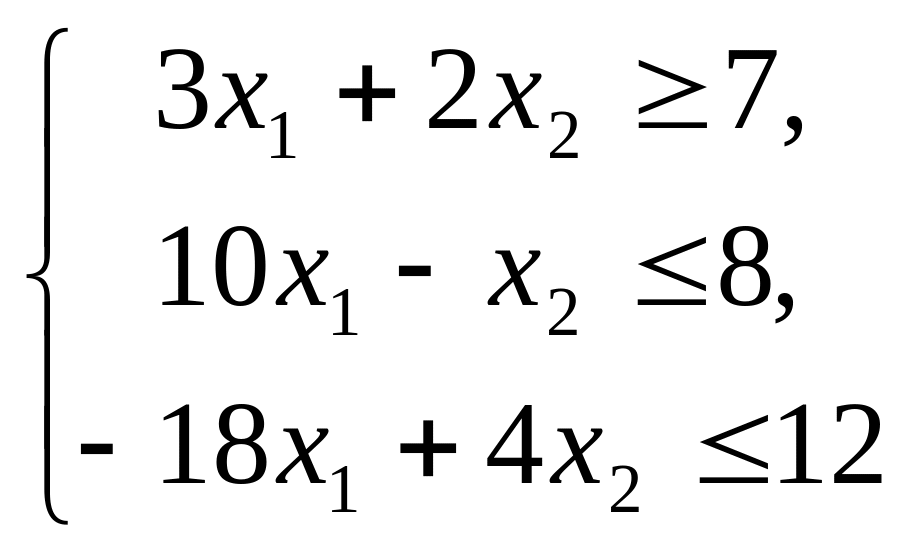(6)
(7)
Решение. Областью допустимых решений задачи (5) - (7) является треугольник ABC (рис. 8.2). Полагая значение целевой функции (5) равным некоторому числу h, получаем линии уровня, а именно окружности:
центром
Е
(3,
4) и радиусом
.
С увеличением (уменьшением) числа h значения функции F соответственно увеличиваются (уменьшаются).
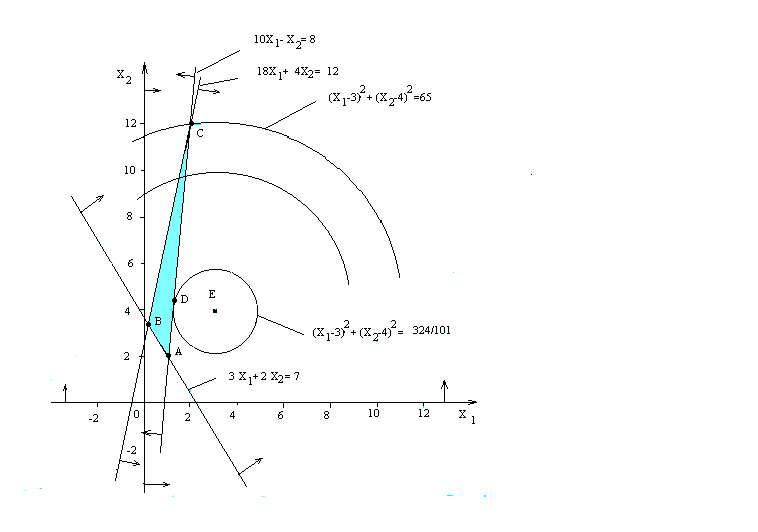
Рис.8.2.
Проводя из точки Е окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке D, в которой окружность касается области решений. Для определения координат этой точки воспользуемся равенством угловых коэффициентов прямой
и
касательной к окружности в точке D.
Из
уравнения прямой
видим, что ее угловой коэффициент в точке D равен 10. Угловой же коэффициент касательной к окружности в точке D определим как значение производной функции в этой точке.
Рассматривая как неявную функцию переменной и дифференцируя уравнение окружности, получим:
откуда
Приравнивая найденное выражение числу 10, получаем одно из уравнений для определения координат точки D. Присоединяя к нему уравнение прямой, на которой лежит точка D, имеем систему:
откуда
.
Таким
образом
.
Как видно из рис. 8.2, целевая функция принимает максимальное значение в точке С (2, 12). Ее координаты определены путем решения системы уравнений прямых, на пересечении которых находится точка С.
Таким
образом, максимальное значение функции
Пример 8.3.
Найти минимальное и максимальное значения функции.
(8)
при условиях:
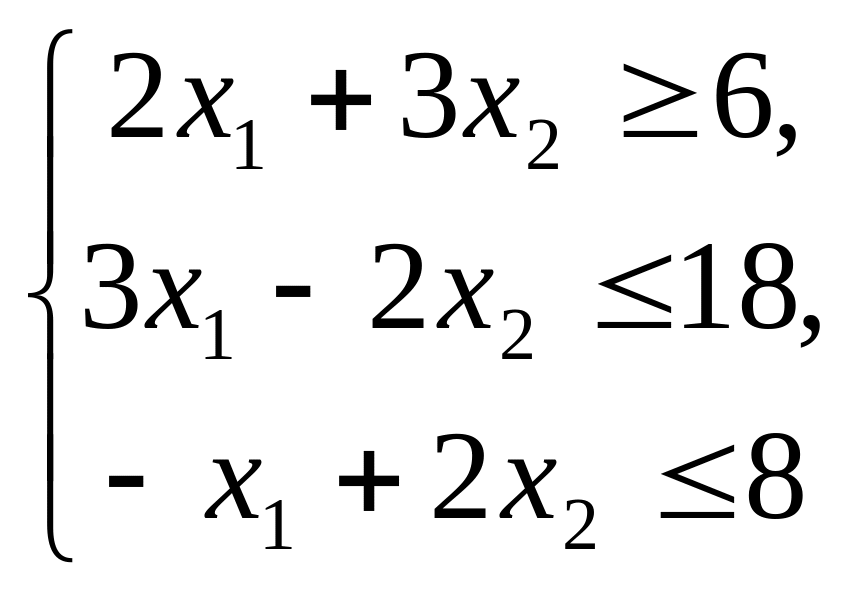(9)
(10)
Решение. Областью допустимых решений исходной задачи является
многоугольник ABCDE (рис. 8.3), а линиями уровня – окружности:
с центром F (4, 3) и радиусом .
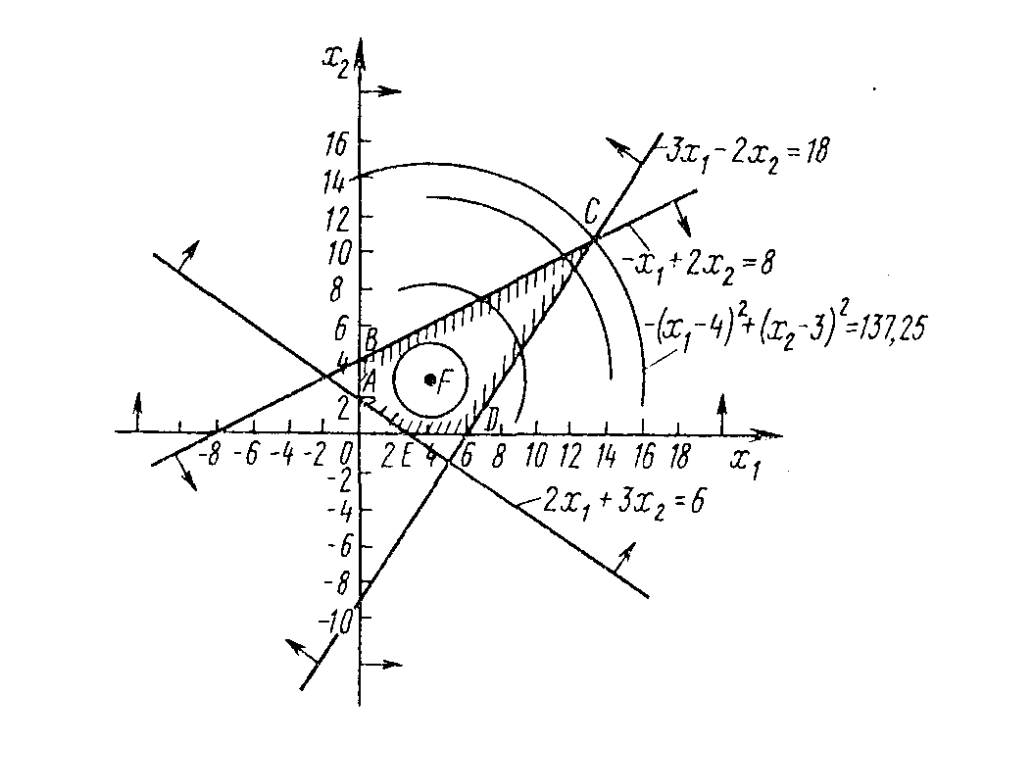
Рис. 8.3.
Из
рис. 8.3 видно, что целевая функция
принимает минимальное значение в точке
F
(4,
3), а максимальное - в точке С
(13,
21/2). Следовательно,
Пример 8.4.
Найти максимальное значение функции.
(11)
при условиях:
(12)
(13)
Решение. Область решений задачи (11) - (13) изображена на рис. 8.4.
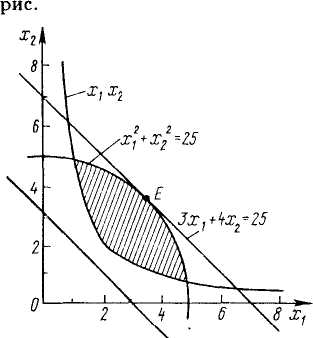
Рис. 8.4.
На этом рисунке построены две линии уровня, представляющие собой
прямые. Из рисунка 8.4 видно, что максимальное значение целевая функция
задачи
принимает в точке Е,
в
которой прямая касается окружности
.
Для определения координат точки Е
воспользуемся
равенством угловых коэффициентов
прямой:
,
(где h - некоторая постоянная) и касательной к окружности в точке Е.
Рассматривая как неявную функцию переменной , почленно дифференцируем уравнение окружности:
.
получим:
или
Приравнивая
найденное выражение числу
,
получаем одно из уравнений для определения
координат точки Е.
В
качестве второго уравнения возьмем
уравнение окружности. Таким образом,
для определения координат точки Е
имеем
систему:
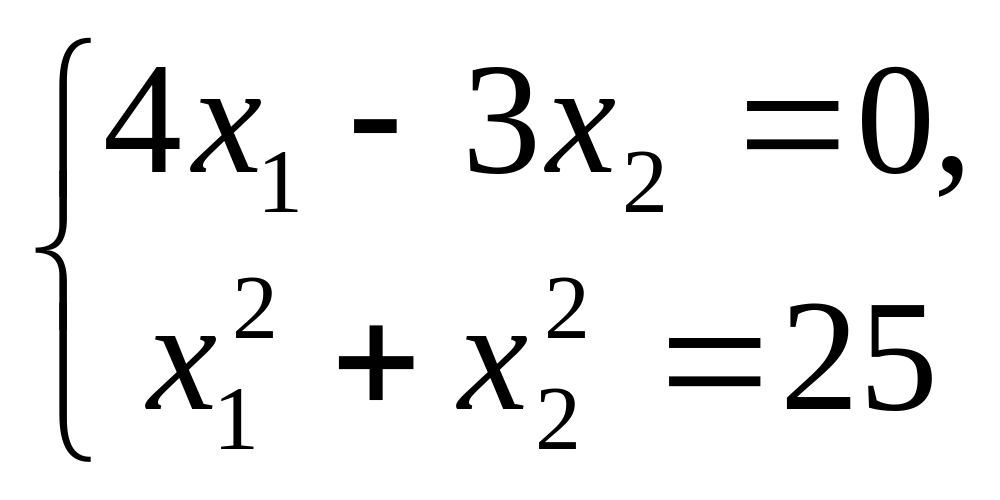
Откуда:
Значит,
Пример 8.5.
Найти минимальное и максимально значения функции:
при условиях:
.
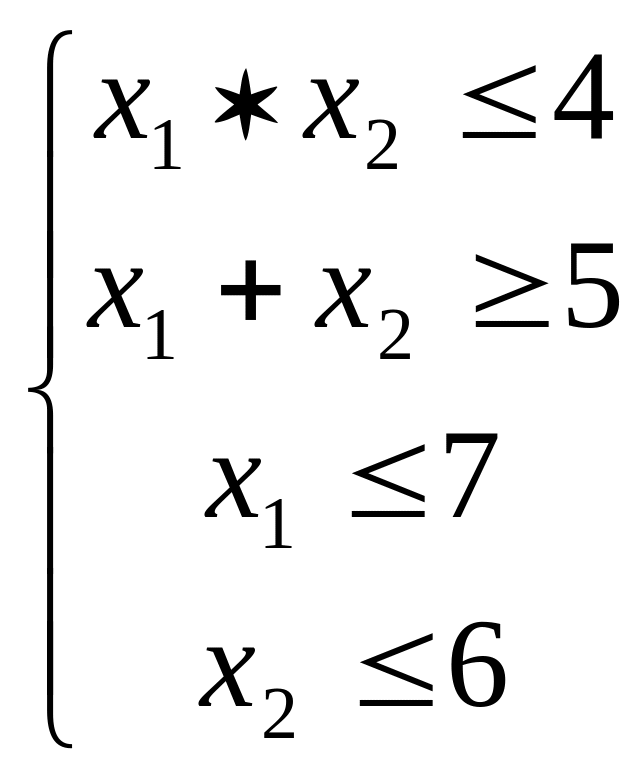
Решение.
В этом случае (рис. 8.5) область допустимых
решений не является выпуклой и состоит
из двух отдельных частей. Минимальное
значение функции
достигается
в точках А
(1;4) и L
(4;1). Функция
имеет
два локальных максимума: в точке D
(2/3;6) функция
и в точке
M
(7;4/7) функция
.
Точка М
является точкой глобального максимума.
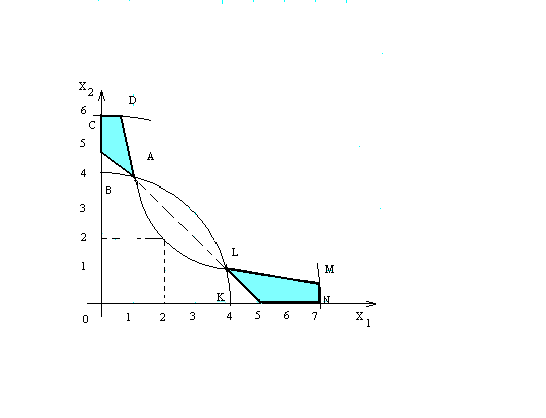
Рис.8.5
Пример 8.6.
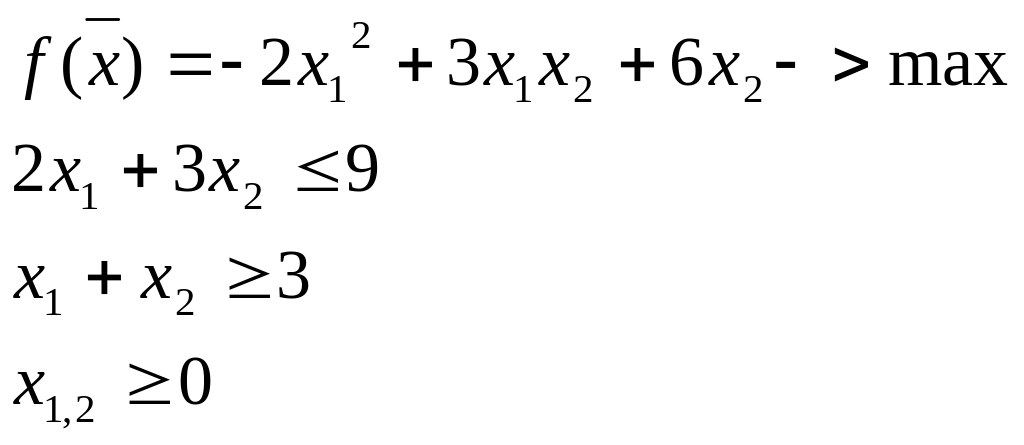
О
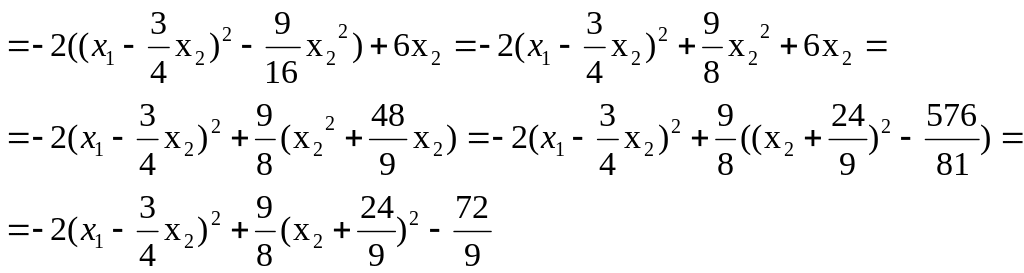пределим
вид линии уровня
с,
для этого приведем
к каноническому виду
П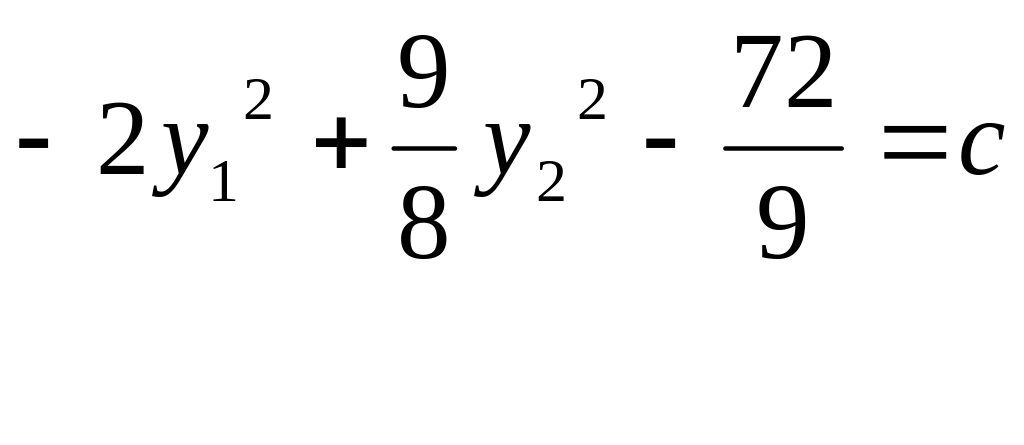
усть
т
огда
Итак, мы привели линию уровня к каноническому виду. Это гипербола.
Например, при с = 0
Построим линии уровня в системе координат (х1, х2).
откуда, выражая х2 через х1 , получим
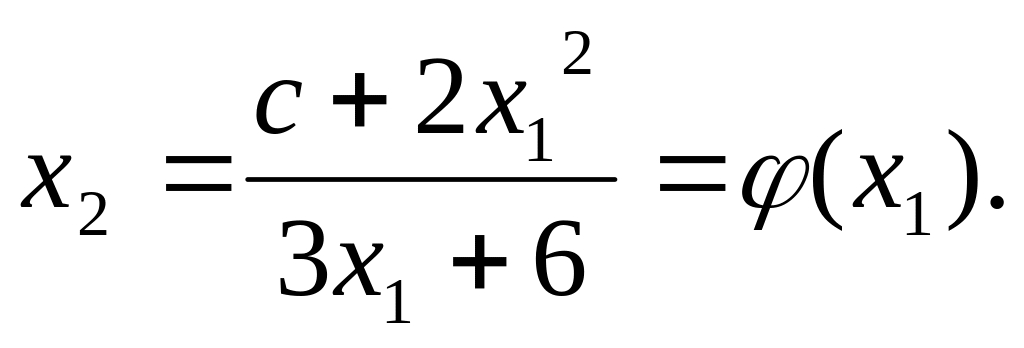
Найдем асимптоты функции.
Вертикальная асимптота - т.к.
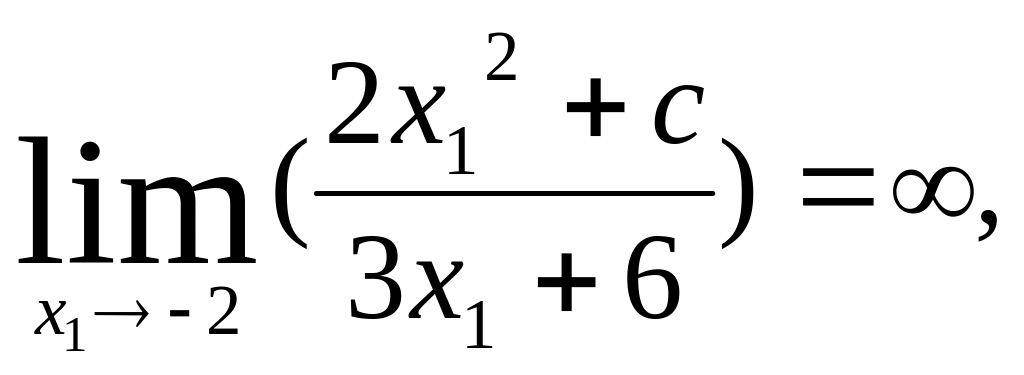
то вертикальная асимптота x1=-2.
Горизонтальная асимптота - т.к.
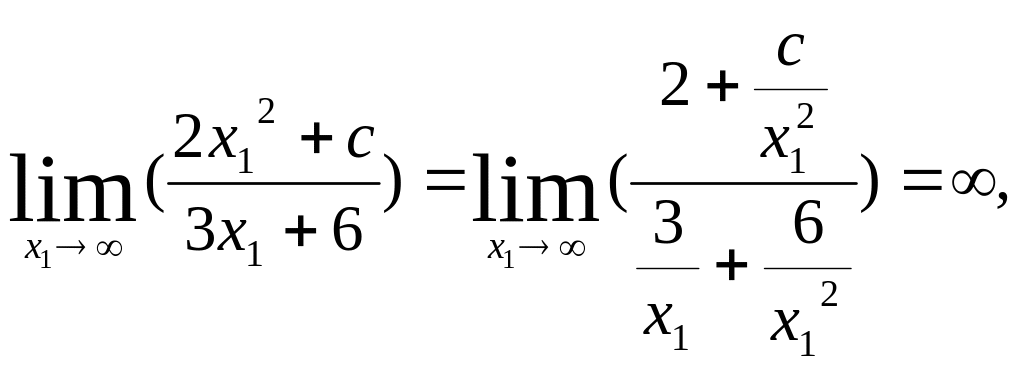
то горизонтальная асимптота отсутствует.
Н
аклонная
асимптота -
где
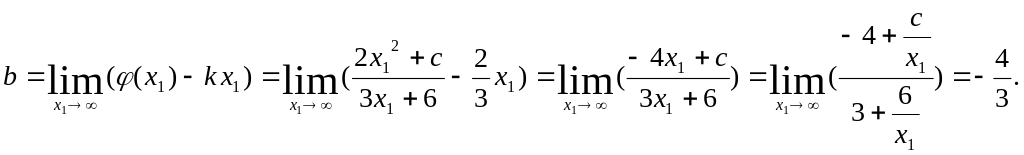
Итак, уравнение наклонной асимптоты
На координатной плоскости поместим ограничения, асимптоты и линии уровня
0; -6
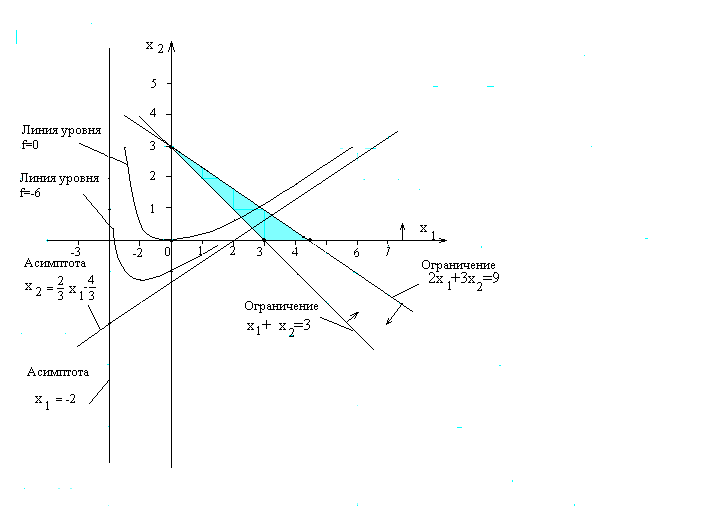
Рис. 8.6
Найдем стационарную точку функции, используя необходимое условие первого порядка
Решая систему методом Гаусса, получим
Проверим, является ли полученная точка точкой экстремума или седловой.
Для этого рассчитаем матрицу Гессе:
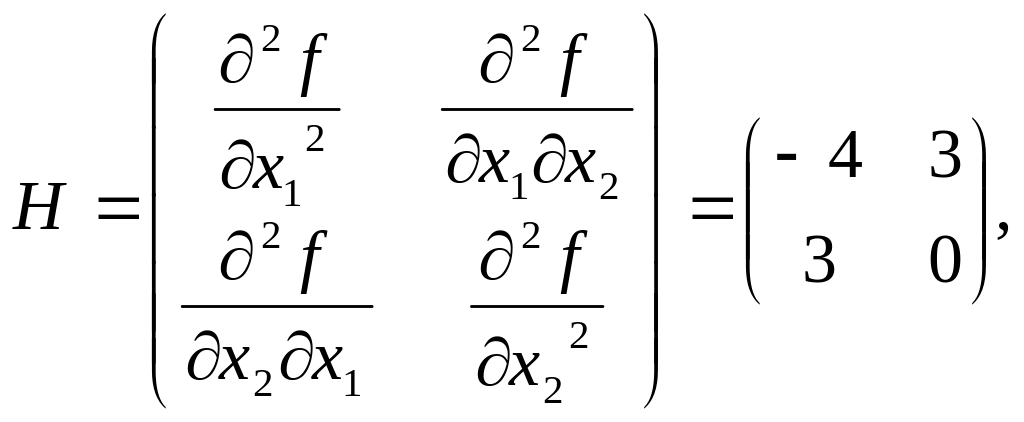
а также ее миноры:
Согласно критерию Сильвестра матрица Гессе не является ни положительно, ни отрицательно определенной, то есть стационарная точка (в которой градиент равен нулю) является седловой.
Т.к. множество планов нашей задачи является ограниченным множеством, то по теореме Вейерштрасса задача имеет решение и оно будет находиться на границе области
Условный максимум будет находиться на границе области (он не может находиться внутри области, т.к. стационарная точка находится вне её).
Как
видно из графика, точка максимума функции
является точкой касания линии уровня
(гиперболы) и ограничения
.
Для этого необходимо построить касательную
к гиперболе, угловой коэффициент которой
будет равен угловому коэффициенту
прямой
.
Тангенс угла наклона касательной к
гиперболе равен производной
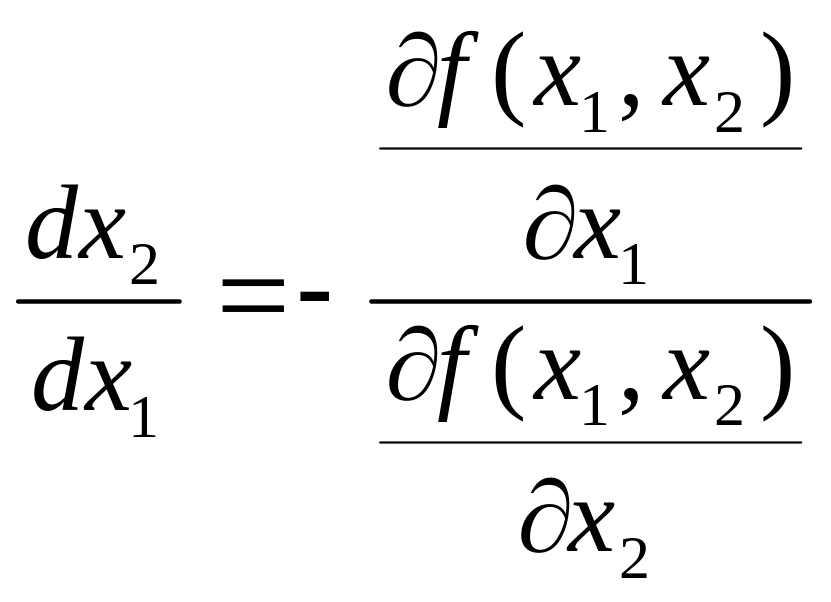
и
уравнение ограничения
Решим эту систему
м
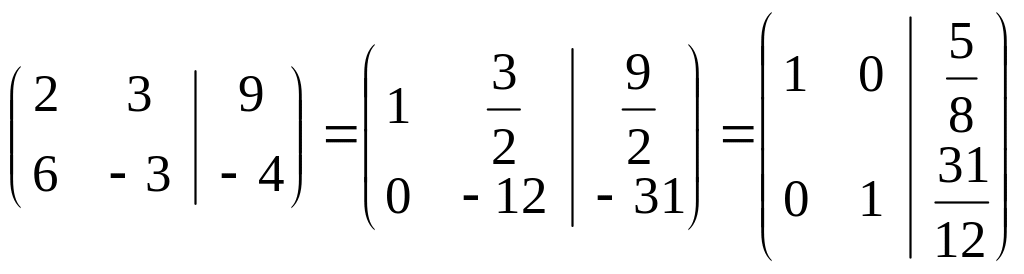етодом
Гаусса, получим
х1 = 5/8; х2 = 31/12.
f(5/8; 31/12) = 19.5625 - максимум функции
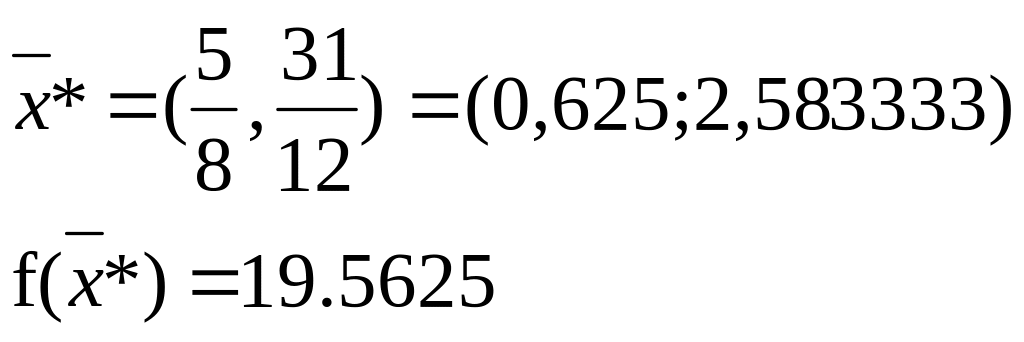
Ответ: