6.3. Классификация знп.

• По числу переменных:

• Задача одномерной оптимизации (ЗОО)

• Задача многомерной оптимизации (ЗМО)

  • По виду ограничений:

    • Задача безусловной оптимизации (ЗБУ)

• Задача условной оптимизации (ЗУО)

ЗУО принципиально сложнее, чем ЗБО.

• По степени гладкости функций, входящих в задачу:

  • гладкие

  • негладкие

• По виду функции (например):

  • Задача квадратичного программирования (ЗКП)

где – симметричная неположительно определенная матрица, – заданный вектор из , – заданная матрица, порядка , .

• Задача выпуклого программирования (ЗВП)

где определены и выпуклы на , определена и вогнута на .

6.4. Классическая оптимизация.

Под классической оптимизацией будем подразумевать тот подход к поиску точек экстремума функции, который основан на дифференциальном исчислении. В данной главе вкратце остановимся на данном подходе (в случае функции одной переменной).

Пусть функция кусочно непрерывна и кусочно гладка на отрезке . Это значит, что на может существовать лишь конечное число точек, в которых либо терпит разрыв первого рода, либо непрерывна, но не имеет производной. Тогда, как известно, точками экстремума функции на могут быть лишь точки, в которых выполняется одно из следующих условий:

1. либо терпит разрыв;

2. либо непрерывна, но производная 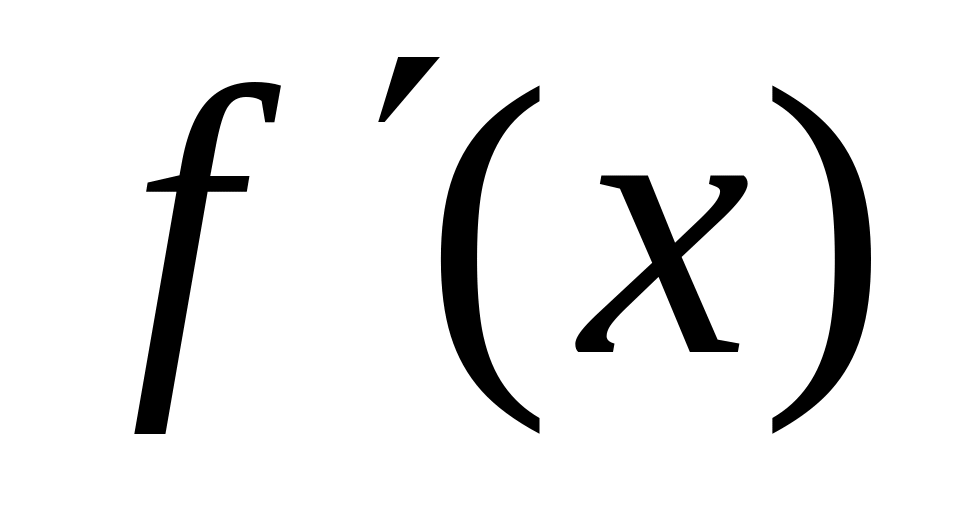не существует;

3. либо производная существует и равна нулю;

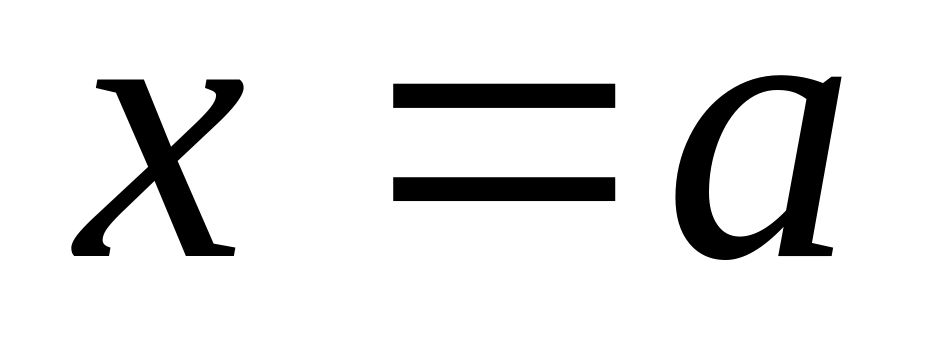4. либо и .

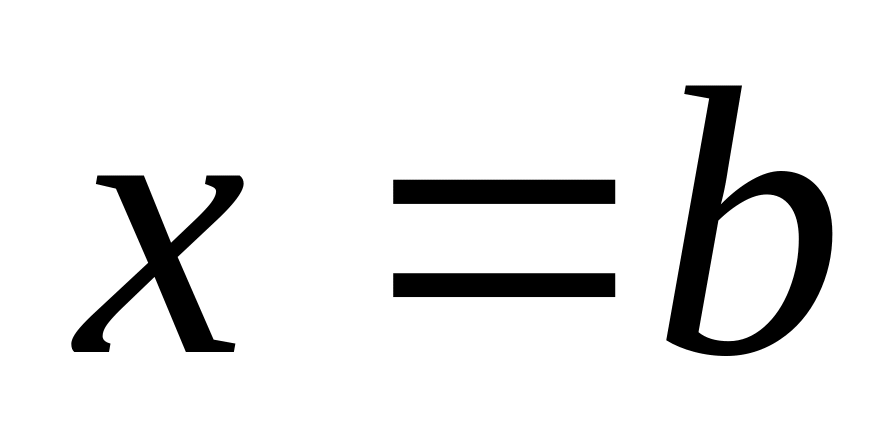Такие точки принято называть точками, подозрительными на экстремум.

Поиск точек экстремума функции начинают с нахождения всех точек, подозрительных на экстремум.

Сформулируем необходимые условия, которым должна удовлетворять точка локального экстремума функции одной переменной.

- необходимое условие первого порядка: для того чтобы точка являлась точкой локального максимума (минимума) на интервале необходимо

• 

- необходимое условие второго порядка:

• 

После того как такие точки найдены, проводят дополнительное исследование и отбирают среди них те, которые являются точками локального минимума или максимума. Для этого обычно исследуют знак первой производной в окрестности (или соответствующей полуокрестности граничных точек и ) подозрительной точки.

В тех случаях, когда удается вычислить в подозрительной точке производные второго и более высокого порядков, то их также можно использовать для исследования поведения функции в окрестности этой точки.

Чтобы найти глобальный минимум или максимум функции на , нужно перебрать все точки локального минимума (максимума) на и среди них выбрать точку с наименьшим (наибольшим) значением функции, если таковое существует.

Если эти условия не выполняются, то не может быть точкой локального максимума (минимума). С другой стороны, если эти условия выполняются, то может и не быть точкой локального максимума (минимума).

Сформулируем достаточные условия, которым должна удовлетворять точка локального экстремума:

• .

Определение 6.9. Стационарной точкой называется точка, в которой . Если стационарная точка не соответствует локальному оптимуму, то она является точкой перегиба или седловой точкой.

Пример 6.7. Исследуем свойства функции .

Вычислим:

1. , откуда очевидно, что стационарными точками являются .

2. .

Так как , то точки являются седловыми. А так как , то является точкой глобального минимума.

Классический метод исследования функции на экстремум следует использовать во всех тех случаях, когда достаточно просто удается выявить все подозрительные на экстремум точки и реализовать описанную выше схему отбора экстремальных точек. К сожалению, классический метод имеет весьма ограниченное применение. Дело в том, что вычисление производной в практических задачах зачастую является непростым делом. Например, может оказаться, что значения функции определяются из наблюдений или каких-либо физических экспериментов, и получить информацию о ее производной крайне сложно. Но даже в тех случаях, когда производную все же удается вычислить, решение уравнения и выявление других точек, подозрительных на экстремум, может быть связано с серьезными трудностями. Поэтому важно иметь также и другие методы поиска экстремума, не требующие вычисления производных, более удобные для реализации на современных ЭВМ.

Обобщим выше сказанное на случай функции конечного числа переменных, т.е. будем считать, что Р есть не пустое множество из , а - функция, определенная на этом множестве. Все определения, данные в параграфе 6.2, справедливы и в данном случае.

Сформулируем необходимые и достаточные условия, которым должна удовлетворять точка локального экстремума функции n переменных.

Необходимые условия, которым должна удовлетворять точка локального экстремума:

- необходимое условие первого порядка: для того чтобы точка являлась точкой локального максимума (минимума) , необходимо

- необходимое условие второго порядка:

- отрицательно полуопределенная матрица (положительно полуопределенная матрица).

Если эти условия не выполняются, то не может быть точкой локального максимума (минимума). С другой стороны, если эти условия выполняются, то может и не быть точкой локального максимума (минимума).

Сформулируем достаточные условия, которым должна удовлетворять точка локального экстремума:

- отрицательно определенная матрица (положительно определенная матрица).

Напомним, что - n-мерный вектор первых производных , а - симметрическая матрица порядка вторых частных производных .

Пример 6.8. Рассмотрим функцию

Требуется классифицировать точку .

Так как

то , и следовательно стационарная точка.

Определим матрицу :

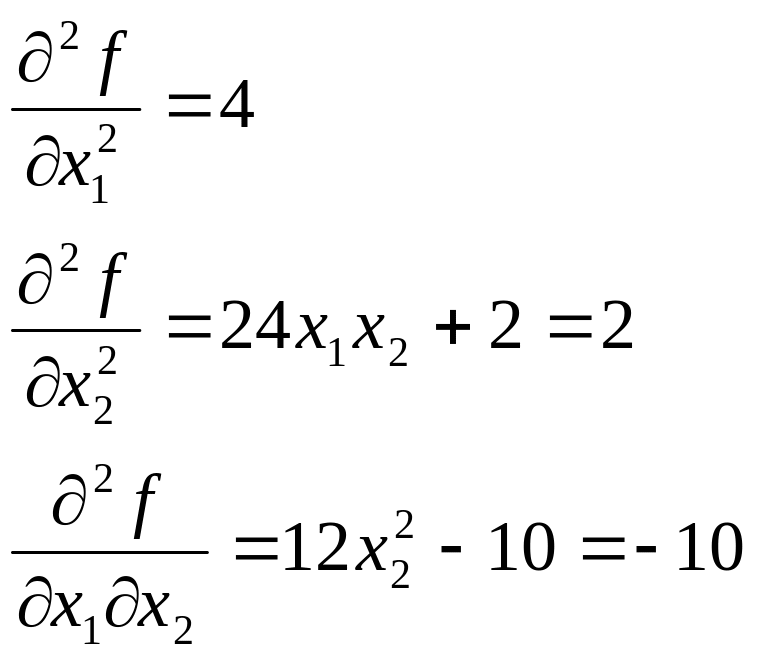
Следовательно, = .

По критерию Сильвестра матрица является неопределенной, так как . Следовательно, представляет собой седловую точку.