3. Ускорение

При движении тела скорость может быть не постоянна. Быстрота изменения скорости характеризуется ускорением. Ускорение, по определению, равно отношению бесконечно малого изменения вектора скорости ко времени dt этого изменения:

. (1.6)

То есть ускорение – это вектор­, равный первой производной от вектора скорости по времени. Через проекции вектора ускорения на декартовы оси координат , вектор полного ускорения равен . Величина полного ускорения по теореме Пифагора равна .

Кроме этого, принято представлять полное ускорение как векторную сумму составляющих ускорения на касательное и нормальное направление к траектории . Их называют соответственно касательным (тангенциальным) и нормальным (центростремительным) ускорениями. Величина полного ускорения равна .

Представим вектор скорости, который направлен по касательной, как произведения модуля скорости на единичный вектор касательной . Определим ускорение как первую производную от этого произведения по времени

. (1.7)

Первый член формулы характеризует изменение скорости по величине и определяет касательное ускорение . Второй член формулы определяет скорость поворота единичного вектора и характеризует изменение скорости по направлению. Это нормальное ускорение, которое направлено к центру кривизны траектории.

В ыведем формулу нормального ускорения. Разложим вектор полного изменения скорости на составляющие: на нормаль и на касательную к траектории (рис. 1.2). При бесконечно малом перемещении дугу dS можно принять за отрезок. Заштрихованные равнобедренные треугольник расстояний и треугольник скоростей подобны, Условие подобия . Подставим сюда путь , получим

. (1.8)

4. Уравнения равнопеременного движения

Движение точки называется равнопеременным, если вектор ускорения постоянен.

Так как, исходя из определения ускорения, элементарное приращение скорости равно , то полное изменение вектора скорости за конечное время равно сумме элементарных приращений скорости, т.е. равно интегралу от ускорения по времени . Откуда скорость в момент времени t может быть определена по уравнению

. (1.9)

Элементарное изменение радиус-вектора точки, по определению скорости, равно . Полное изменение вектора перемещения за конечное время будет равно сумме элементарных приращений, то есть будет равно интегралу от вектора скорости по времени . Откуда, радиус – вектор равен

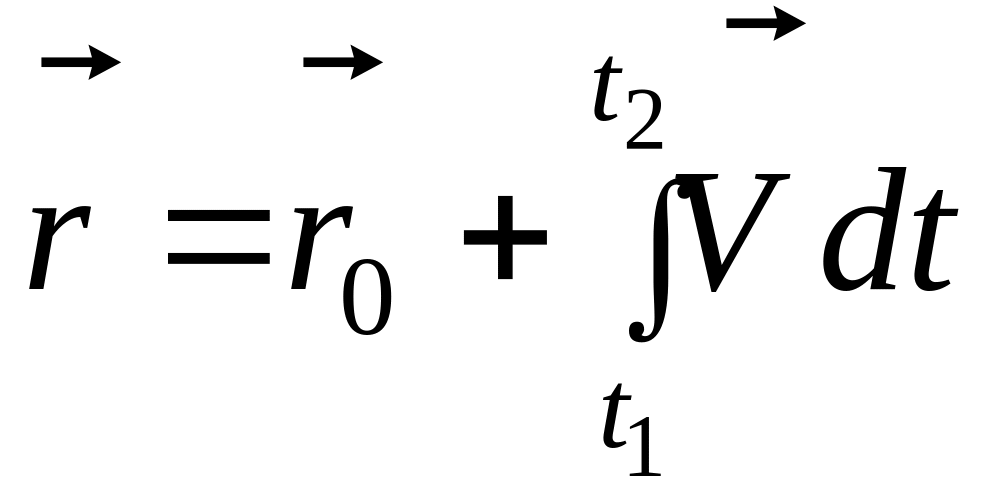(1.10)

Применим эти уравнения для вывода скорости и радиус-вектора точки при равнопеременном движении. Равнопеременное движение – это движение с постоянным по величине и по направлению ускорением. Например, полет тела в поле тяжести Земли с ускорением свободного падения g = 9,81 м/с².

Получим уравнение для скорости. Для этого проинтегрируем уравнение (1.9) при постоянном векторе ускорения, , в результате получим

. (1.11)

Подставив формулу скорости (1.11) под знак интеграла для вектора перемещения, получим основное кинематическое уравнение равнопеременного движения

. (1.12)

При решении конкретных задач векторные уравнения (1.11) и (1.12) проецируют на выбранные оси координат и получают систему уже алгебраических уравнений для решения задачи.