
- •Математический факультет Кафедра вычислительной математики и программирования
- •Содержание
- •2 Разностные методы решения задач математической физики….…..20
- •Разностные схемы для линейных дифференциальных уравнений
- •1 Математические модели физических систем
- •1.1 Физические системы и методы их исследования
- •Основные определения и понятия
- •Системы деформируемых твёрдых тел
- •1.1.3 Подходы к исследованию систем деформируемых твёрдых тел
- •1.1.4 Средства исследования состояния систем деформируемых твёрдых тел
- •Разностные схемы для основных уравнений математической физики
- •1.2.1 Основные уравнения математической физики и их классификация
- •1.2.2 Разностная аппроксимация основных производных. По определению производная функции одной переменной записывается в виде
- •Это значит, что аппроксимация
- •Общий принцип метода сеток
- •Сходимость, аппроксимация и устойчивость разностных схем
- •2 Разностные методы решения задач математической физики
- •2.1 Разностные схемы для линейных дифференциальных уравнений
- •2.1.1 Краевые задачи для линейных дифференциальных уравнений
- •2.1.2 О задаче Дирихле
- •2.1.3 Разностные аппроксимации уравнений эллиптического типа
- •2.1.4 Разностная аппроксимация граничных условий
- •2.2 Построение разностной аппроксимации задачи Дирихле для
- •2.2.1 Разностная схема задачи Дирихле для уравнения Пуассона.
- •2.2.2 Устойчивость и сходимость разностной задачи Дирихле
- •2.3. Разрешимость разностных уравнений и способы их решения. Правило Рунге
- •2.4. Разностные схемы для линейных дифференциальных
- •2.5. Разностные схемы для линейных дифференциальных уравнений
- •2.5.1. Общая постановка задачи.
- •3. Метод конечных элементов и суперэлементов
- •3.1. Физические предпосылки методов
- •3.2 Деформации твёрдых тел
- •3. 2.1 Линейно-упругие деформации твёрдых тел
- •3.2.2. Нелинейно-упругие деформации твёрдых тел
- •3.3. Прикладные вопросы метода конечных элементов
- •3.3.1. Основная концепция метода конечных элементов
- •3.3.2 Дискретизация и оптимальная нумерация узлов области
- •3.3.3. Метод конечных элементов в теории упругости.
- •3..4 Построение конечно - элементных соотношений
- •3.5. Аналитический алгоритм метода конечных элементов для исследования
- •Свойства матрицы жёсткости
- •3.7 Аналитический алгоритм метода суперэлементов
- •Методы исследования нелинейных математических
- •4.1 Общие предпосылки методов численного исследования нелинейных
- •4.2 Итерационные численные методы
- •4.3 Безитерационные методы исследования нелинейных математических моделей деформируемых твёрдых тел и их систем
- •4.4 Сравнительный анализ эффективности методов исследования
- •5 Основы методологии компьютерного объектно-
- •5.1 Основные понятия и определения
- •5.2 Построение виртуальной физической модели системы
- •5.3 Исходные данные при компьютерном моделировании
- •5.4 Деформации грунтовых оснований при устройстве отдельных
- •6 Технология компьютерного объектно-
- •6.1 Технологические этапы компьютерного объектно-ориентированного
- •6.2 Интерфейс визуального ввода данных
- •7 Программное обеспечение компьютерного
- •7.1 Структура программного обеспечения объектно-ориентированного моделирования системы деформируемых твёрдых тел
- •7.2 Технология объектно-ориентированного программирования
- •Объектно-ориентированного моделирования физической системы
- •7.3 Программный комплекс «Энергия - 2д » моделирования
- •7.4 Программный комплекс «Энергия - ос » моделирования
- •7.5 Программный комплекс «Энергия - 3д » моделирования
- •8 Верификация технологии и программного
- •8.1 Методологические аспекты верификации
- •8.2 Верификация технологии и программного обеспечения
- •8.3 Верификация технологии и программного обеспечения
- •8.4 Верификация технологии и программного обеспечения
- •Численные методы математической физики
- •1. Метод сеток для задачи дирихле
- •1.1. Основы метода сеток
- •1.3.Варианты задания
- •Лабораторная работа №2
- •Дополнение к лабораторной работе №2
- •Лабораторная работа №3 Метод сеток для уравнения параболического типа.
- •Лабораторная работа №4 Метод сеток для уравнения гиперболического типа
2.4. Разностные схемы для линейных дифференциальных
уравнений параболического типа. Решение задачи Коши.
Вопросы построения и исследования разностных схем, возникающих при решении параболических уравнений методом сеток, рассмотрим на примере задачи Коши для уравнения теплопроводности
![]() (2.28)
(2.28)
с условием на прямой t = 0
и(х, 0) = ψ(x), (2.29)
Требуется
найти функцию и
(х, t),
которая
при t
> 0 и
![]() удовлетворяла бы
удовлетворяла бы
уравнению (2.28), а при t = 0 выполняла бы условие (2.29). Будем считать, что задача (2.28) , (2.29) имеет в верхней полуплоскости единственное решение и(х, t), непрерывное вместе со своими производными. Запишем задачу (2.28) , (2.29) в виде L(u) = f. Для этого достаточно положить
L(u)
≡
![]()
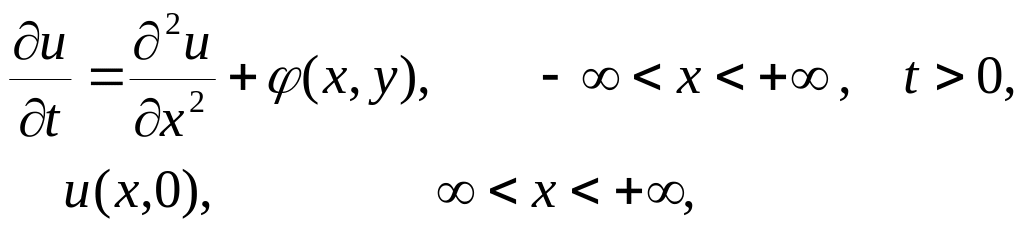
f
≡
![]()
![]()
Будем далее считать, что t изменяется в пределах 0 ≤ t ≤ T < + .
В рассматриваемом случае
D = {- < х < +, 0 < t ≤ T}, Г - объединение прямых t= 0 и t= T.
Выберем прямоугольную сетку и заменим область = D + Г сеточной областью Dh. К области Dh отнесем совокупность точек (узлов) (хт, tn ), координаты которых определяются по правилу
xm = mh, т = 0, ± 1, ±2, ..., h>0,
tn = n , п = 0, 1, ..., N, >0, N ≤ T< (N+).
Заменим
задачу L(u)
= f
разностной
схемой вида Lh(u(h))
= f
(h).
Обозначим
через и(
хт,
tn
)
точное
значение решения задачи L(u)=f
в
узле (хт,
tn
),
через
![]() — соответствующее приближенное
сеточное значение. Для замены
дифференциальных операторов разностными
воспользуемся формулами численного
дифференцирования.
— соответствующее приближенное
сеточное значение. Для замены
дифференциальных операторов разностными
воспользуемся формулами численного
дифференцирования.
(2.31)
(2.30)
(2.32)
(2.33)
некоторое время употреблялся в вычислительной практике.
Однако в настоящее время он не используется, так как оказалось, что соответствующая ему разностная схема неустойчива при любом выборе шага h — по пространству и шага —по времени.
2.5. Разностные схемы для линейных дифференциальных уравнений
гиперболического типа
2.5.1. Общая постановка задачи.
Будем рассматривать линейные дифференциальные уравнения 2-го порядка гиперболического типа. Такие уравнения часто встречаются в физических задачах, связанных с переносом энергии и с процессами колебаний. Метод сеток для уравнений гиперболического типа по своей структуре имеет много общего с методом сеток для уравнений эллиптического и параболического типов.
Мы уделим основное внимание типичному и наиболее простому по виду уравнению с постоянными коэффициентами гиперболического типа — волновому уравнению
![]() ,
(2.34)
,
(2.34)
где f (х, у) — известная функция, которую мы будем считать дважды непрерывно дифференцируемой в некоторой нижеуказываемой области D.
В связи с уравнением (2.34) будем рассматривать следующие задачи.
Задача Коши. В области D = { y > 0, - оо < х < + оо } найти дважды непрерывно дифференцируемую функцию и (х, у), которая в этой области удовлетворяла бы уравнению (2.34), а на прямой у = 0 — начальным условиям
и(х,
0)
= φ(x),
![]() (2.35)
(2.35)
где φ и ψ —заданные функции.
Смешанная граничная задача. В области D = { y>0, α < х < β} найти дважды непрерывно дифференцируемую функцию и (х, у), которая в этой области удовлетворяла бы уравнению (2.34), а на границе Г области D при у = 0 — начальным условиям (2.35) и при х = α, х = β — одному из трех граничных условий:
а) (условиям первого рода)
и (a, y) = μ1(y), u(β, y) = μ2(y); (2.36)
б) (условиям
второго рода)
(2.37)
(
2.38)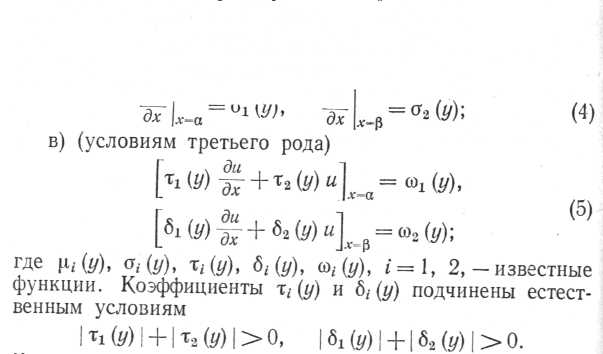
![]() =
σ1(y)
,
=
σ1(y)
,
![]() =σ2(y)
,
=σ2(y)
,
Отметим, что условия (2.36) и (2.37) являются частным случаем условий (2.38).
2.5.2. Решение задачи Коши. Рассмотрим метод сеток решения задачи Коши для дифференциального уравнения (2.67) с начальными условиями (2.68).
Выберем прямоугольную сетку, положив
xm = mh, m = 0, ±1, ±2, ..., yn = п1, n = 0, 1, 2....., h > 0, l > 0.
Рассмотрим трехслойный пятиточечный шаблон и в соответствии с этим шаблоном
определим
множество
![]() внутренних узлов и множество Гh
граничных узлов.
внутренних узлов и множество Гh
граничных узлов.
(m,n+1) К множеству отнесем узлы (хт, у„) D, к множеству Гh
 отнесем
узлы, лежащие на
прямой
у
= 0.
Вся сеточная область
отнесем
узлы, лежащие на
прямой
у
= 0.
Вся сеточная область
(m-1,n) (m,n) (m+1,n) на Dh = D°h + Гh будет состоять из узлов (хт, yn) = D +Г .
 Используя взятый шаблон и формулу для
замены
Используя взятый шаблон и формулу для
замены![]() ,
,
(m,n-1) получим разностную схему
где

Эта схема аппроксимирует уравнение (2.67)с погрешностью 1 порядка O(l2+h2) а начальные условия - с погрешностью порядка 0(l).
