Лабораторная работа №4 Метод сеток для уравнения гиперболического типа

Постановка задачи. Используя метод сеток, составить решение смешанной задачи для уравнения колебания струны

с начальными условиями u(x,0) = f(x), u_t (х,0) = Ф(х) (0 ≤ х ≤ 1) и

краевым условиями u(0, t) = (t), u(1, t) = (t).

Решение выполнить с шагом h = 0,1; 0 ≤ t ≤ 0,5.

Теоретические основы метода решения задачи

Рассмотрим смешанную задачу для уравнения колебания струны, заключающуюся в отыскании функции, удовлетворяющей уравнению

(4.1)

а также начальным условиям

u(x,0) = f(x), u_t (х,0) = Ф(х) (0 ≤ х ≤ s) (4.2)

и краевым условиям

u(0, t) = (t), u(s, t) = (t), (4.3)

Так как введение переменной  = at приводит уравнение (4.1) к виду

(4.4)

то в дальнейшем можем принять а =1.

Построив в полуполосе t  O, 0 ≤ х ≤ s (рис. 4.1) два семейства параллельных прямых

x = ih (i = 0,1,2, ..., n), t = j l (j = 0,1,2, .. .),

заменяем производные в уравнении (4.4) разностными отношениями.

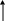
t

	h	(i,j+1)
(i-1,j)	(l, j)	l	(i+1,j)
	(i,j-1)

s

Рис. 4.1

Пользуясь симметричными формулами для производных, будем иметь

(4.5)

Обозначив  = l / h, получим разностное уравнение

(4.6)

Доказано, что при  ≤ l это разностное уравнение устой­чиво.

В частности, при  = 1 уравнение (4.6) имеет наиболее простой вид:

. (4.7)

Заметим, что для получения уравнения (4.6) была использована схема узлов, отмеченных на рис. 4.1. Эта схема является явной, так как уравнение (4.6) позволяет найти значения функции и (x, t) на слое t _j+1, если известны значения на двух предыдущих слоях. Для того чтобы найти приближенное решение задачи (4.1) - (4.3), не­обходимо знать значения решения на двух начальных слоях. Их можно найти из начальных условий. Существует три подхода к решению задачи, рассмотрим наиболее употребительный из них.

Заменяем производную u_t (x,0) разностным отношением , где u_{i, -1}

значения функции u(x,t) на слое j = -1. Тогда из начальных условий (4.2) будем иметь

u_i0 = f_i , = Ф_i. (4.8)

Напишем разностное уравнение (4.7) для слоя j = 0:

(4.9)

Исключив из уравнений (4.8), (4.9) значения u_i,-1 получим

u_i0 = f_i,, , (4.10)

причём x_i =0+ ih, (i = 0,1,2, ..., n), n = t_j =0+ jh (j = 0,1,2, .. .),

Замечание. Аналогичным образом применяется метод сеток при ре­шении смешанной краевой задачи для неоднородного уравнения.

Пример. Методом сеток найти решение задачи (4.1) – (4.4) при условии

f(x) = 2x(1-x²), Ф(x) = (x+0,4)cos(x+0,3), (t) = 0,5t², (t) = 0.

Решение по указанным формулам удобно выполнить в таблице, которая и является решением данной задачи.

Порядок заполнения таблицы:

1. Вычисляем значения u_i0=f(x_i) = 2x_i(1— x_i ²) при х _i = 0,1i и записы­ваем их в первую строку (она соответствует значению t₀ ⁼ 0).

2. Вычисляем значения u_0j = (t_j) = 0,5t_j² при t_j = 0,1 и записываем их в первый столбец таблицы (он соответствует значению х_о = 0).

xi tj	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1.0
0	0	0,198	0,384	0,546	0,672	0,750	0,768	0,714	0,576	0,342	о
0,1	0,005	0,2381	0,4247	0,5858	0,7092	0,7677	0,7942	0,7315	0,5825	0,3354	о
0,2	0,02	0,2317	0,4399	0,5879	0,6815	0,7534	0,7312	0,6627	0,4909	0,2405	0
0,3	0,045	0,2218	0,3949	0,5356	0,6321	0,6450	0,6219	0,4906	0,3207	0,1555	0
0,4	0,08	0,2082	0,3175	0,4391	0,4991	0,5006	0,4044	0,2799	0,1552	0,0802	0
0,5	0,125	0,1757	0,2524	0,2810	0,3076	0,2585	0,1586	0,6090	0,0394	-0,0003	0

3. Заносим значения u_10j = (t_j) = 0 в последний столбец таблицы (он соответствует значению x₁₀ = 1,0).

4. Вычисляем значения и_{i 1} по формуле , где f_i+1 и f_i-1 берутся из первой строки таблицы, а Ф_i = (x_i+0,4)cos(x_i+0,3), x_i = 0,1i; i =1, 2, ..., 9); h = 0,1.

Результаты записываем во вторую строку таблицы.

5. Вычисляем значения u_ij в последующих строках по формуле , где значения u_i+1,J, u_i-1,J, u_i,,J-1 берутся из двух предыдущих строк таблицы.

Варианты задания

№1. f(х)=х(х+1), №2. f(х)= x cos πх ,

Ф(x) = cosx, Ф(x) = х(2-х),

(t) = 0, (t) = 2i,

(t) = 2(t+1). (t) = -1.

№ 3. f(х)= cos х(х+1), № 4. f(х)= cos х(х+1),

Ф(x) = x², Ф(x) = sin(x+0.2),

(t) = 2t+1, (t) = t - 0,5,

(t) = 0. (t) = 3t,

№5. f(х) = 2х(х+1)+0,3; № 6. f(х)= (x+0.2)sin ,

Ф(x) = 2sinx, Ф(x) = 1+x²,

(t) = 0,3; (t) = 0,

(t) = 4,3+t. (t) = 1,2(t+1).

№ 7. f(х)= x sinx πх, № 8. f(х) = 2х(х+1)+0,3

Ф(x) = (х+1)², Ф(x) = cos(x+0,5),

(t) = 2t, (t) = 2t,

(t) = 0. (t) = 0.

№ 9. f(х)= х(2х-0,5), № 10. f(х)= (x+1) sinx πх

Ф(x) = cos2x, Ф(x) = x² +x,

(t) = t ², (t) = 0,

(t) = 1,5. (t) = 0,5t.

№ 11. f(х)= (1-х) cos 0,5πх, № 12. f(х)= 0,5x(x+1)

Ф(x) = 2x+1, Ф(x) = x cosx,

(t) = 2t + 1, (t) =2 t ²,

(t) = 0. (t) = 1.

55