10.4. DISCRETE INTERVENTION

319

Table 10.1: SMM Estimates of Krugman Target-Zone Model (units in percent) with deutschemark as base currency.

	η	σ	α	f¯	χ2
					1
Currency	(s.e.)	(s.e.)	(s.e.)	(s.e.)	(p-value)
Belgian	0.697	0.865	1.737	2.641	11.672
franc	(69.01)	(83.98)	(327.1)	(334.3)	(0.001)
French	0.007	0.117	6.045	2.44	12.395
franc	(0.318)	(1.759)	(1590)	(67.88)	(0.000)
Dutch	2.484	2.240	4.152	5.393	11.35
guilder	(1.317)	(0.374)	(146.19)	(5.235)	(0.001)

10.4Discrete Intervention

Flood and Garber [56] study a target-zone model where the authorities intervene by placing the fundamentals back in the middle of the band after one of the bands are hit. If the band width is β = f¯ − f and either f¯ or f is hit, the central bank intervenes in the foreign exchange market by resetting f = f¯ − β/2. Because the intervention produces a discrete jump in f, the central bank loses foreign exchange reserves when f¯ is hit and gains reserves when f is hit.

˜		λ1f¯	˜
	≡ Ae			≡ Be	λ2f
Letting A			and B					, rewrite the solution (10.33)

explicitly as a function of the bands f and f¯

¯		˜ λ1(f−f¯)	˜	λ2	(f−f)
G(f|f, f) = f + αη + Ae			+ Be					.

Impose the symmetry conditions, η = 0 and f = f¯.

λ1 = −λ2		2		˜			−	˜
	= λ = 2/(ασ		) > 0, and B =					A > 0.
written as	q
	G(f|f, f¯) = f + B˜ he−λ(f−				f	) − e−λ(f¯−f)i

(10.43)

It follows that

(10.43) can be (215)

.(10.44)

Under the symmetry assumptions you need only one extra side-condition

˜

to determine B. We get it by looking at the exchange rate at the instant t0 that f(t) hits the upper band f¯

¯ ¯ ¯			˜	−λβ	− 1].	(10.45)
s(t0) = G[f|f, f] = f + B[e

320	CHAPTER 10. TARGET-ZONE MODELS

Market participants know that at the next instant the authorities will reset f = 0. It follows that

Et0 s(t0 + dt) = s(t0 + dt) = G[0|f, f¯] = 0.			(10.46)

To maintain international capital market equilibrium, uncovered interest parity must hold at t0.6 The expected depreciation at t0 must be Þnite which means there can be no jumps in the time-path of the exchange rate. It follows that

lim s(t0 + ∆t) = s(t0),

∆t→0

which implies s(t0) = s(t0 + dt) = 0. Adopt a normalization by setting s(t0) = 0 in (10.45). It follows that

B˜ =	−β	.
	2[e−λβ − 1]

But if s(t0 + dt) = G(0|f, f¯) = 0 and s(t0) = G(f¯|f, f¯) = 0, then

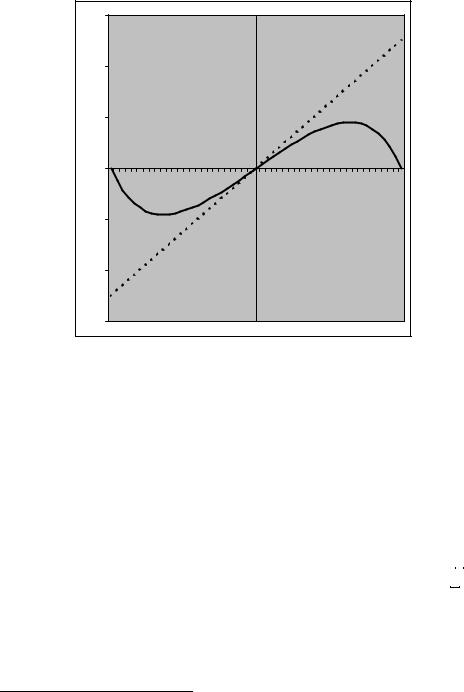
there are at least two values of f that give the same value of s so the G— function is not one-to-one. In fact, the G—function attains its extrema before f reaches f or f¯ and behaves like a parabola near the bands as shown in Figure 10.2.

As f(t) approaches f¯, it becomes increasingly likely that the central bank will reset the exchange rate to its central parity. This information is incorporated into market participant’s expectations. When f is su ciently close to f¯ this expectational e ect dominates and further movements of f towards f¯ results in a decline in the exchange rate. For given variation in the fundamentals within [f, f¯], the exchange rate under Flood-Garber intervention exhibits even less volatility than it does under Krugman intervention.

10.5Eventual Collapse

The target zone can be maintained indeÞnitely under Krugman-style interventions because reserve loss or gain is inÞnitesimal. Any Þxed

6If it does not, there will be an unexploited and unbounded expected proÞt opportunity that is inconsistent with international capital market equilibrium.

10.5. EVENTUAL COLLAPSE

321

0.03
						s
0.02								s=f
0.01
0
-0.025	-0.02	-0.015	-0.01	-0.005	0	0.005	0.01	0.015	0.02	0.025
-0.01	G(f)									f
-0.02
-0.03

Figure 10.2: Exchange rate and fundamentals under Flood—Garber discrete interventions

exchange rate regime operating under a discrete intervention rule, on the other hand, must eventually collapse. The central bank begins the regime with a Þnite amount of reserves which is eventually exhausted. This is a variant of the gambler’s ruin problem.7

The problem that confronts the central bank goes like this. Suppose the authorities begin with foreign exchange reserves of R dollars. It loses one dollar each time f¯ is hit and gains one dollar each time f is hit. After the intervention, f is placed back in the middle of the [f, f¯] band, where it evolves according to the driftless di usion df(t) = σdz(t) until another intervention is required.

Let L be the event that central bank eventually runs out of reserves, G be the event that it gains $1 on a particular intervention and Gc be

7See Degroot [37].

322 CHAPTER 10. TARGET-ZONE MODELS

the event that it loses a dollar on a particular intervention.8 In the Þrst round, the probability that f hits f¯ is 12 . That is, P(Gc) = 12 . By implication, P(G) = 1 − P(Gc) = 12 . It follows that before the Þrst round starts, the probability that reserves eventually get driven to zero

is	1		1
Pr(L) =		Pr(L|G) +		Pr(L|Gc).	(10.47)
	2		2

(10.47) true before the Þrst round and is true for any round as long as the authorities still have at least one dollar in reserves.

Let pj be the conditional probability that reserves eventually become 0 given that the current level of reserves is j-dollars. For any j ≥ 1,

(10.47) can be expressed as the di erence equation
p	=	1	p		+	1	p		,	(10.48)
		2						j−1
j				j+1		2

with p0 = 1.9 Backward substitution gives p2 = 2p1 − 1, p3 = 3p1 − 2, pk = kp1 − (k − 1), . . ., or equivalently, for k ≥ 2,

pk = 1 − k(1 − p1).

(10.49)

Since pk is a probability, it cannot exceed 1. Upon rearrangement you get

	pk	1
p1 = 1 +		−		→ 1, as k → ∞.	(10.50)
	k		k

but if p1 = 1, the recursion in (10.49) says that for any j ≥ 1, pj = 1. Translation? It is a sure thing that any Þnite amount of reserves will eventually be exhausted.

10.6Imperfect Target-Zone Credibility

The discrete intervention rule is more realistic than the inÞnitesimal marginal intervention rule. But if reserves run out with probability 1,

8G is the event that f hits f, and Gc is the event that f hits f¯.

9Clearly, p0 = 1 since if j = 0, reserves have been exhausted. If j = 1, there is a probability of 12 that reserves are exhausted on the next intervention and a probability of 12 that the central bank gains a dollar and survives to play again at which time there will be a probability of p2 that reserves will eventually be exhausted. That is, for j = 1, p1 = 12 p0 + 12 p2. Continuing on in this way, you get (10.48).

10.6. IMPERFECT TARGET-ZONE CREDIBILITY

323

there will come a time in any target-zone arrangement when it is no
longer worthwhile for the authorities to continue to defend the zone.
This means that the target-zone bands cannot always be completely
credible. In fact, during the twelve years or so that the Exchange Rate
Mechanism of the European Monetary System operated reasonably well
(1979—1992), there were eleven realignments of the bands. It would be
strange to think that a zone would be completely credible given that
there is already a history of realignments.
We now modify the target-zone analysis to allow for imperfect cred-
ibility along the lines of Bertola and Caballero [8]. Let the bands for the
fundamentals be [f, f¯] and let β = f¯− f be the width of the band. If
the fundamentals reach the lower band, there is a probability p that the
authorities re-align and a probability 1 − p that the authorities defend
the zone.
If re-alignment occurs, what used to be the lower band of the old
zone f, becomes the upper band of the new zone [f −β, f]. The realign-
ment is a discrete intervention that sets f = f − β/2 at the midpoint
of the new band. If a defense is mounted, the fundamentals are re-
turned to the midpoint, f = f + β/2. An analogous set of possibilities
describe the intervention choices if the fundamentals reach the upper	(217)
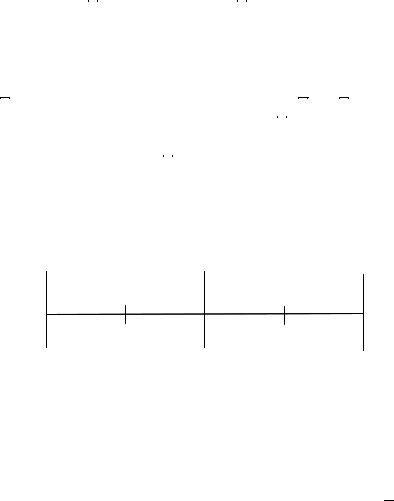
band. Figure 10.3 illustrates the intervention possibilities.

Realign

Defend

f	- b	f	- b/2	f		f	+ b/2	f	+ b

Figure 10.3: Bertola-Caballero realignment and defense possibilities.

We begin with the symmetric exchange rate solution (10.44) with η = 0 and an initial symmetric target zone about 0 where f = −f¯,

	324		CHAPTER 10.				TARGET-ZONE MODELS
(218)	λ1 = −λ2 = λ = q			> 0, and B˜ = −A˜ > 0.
			2/(ασ2)							¯
		˜
	To determine B, suppose that f hits the upper band f at time t0.
	Then
		¯ ¯ ¯					˜	−λβ	− 1).	(10.51)
		s(t0) = G(f|f, f) = f + B(e

At the next instant t0 + dt, the authorities either realign or defend

s(t0 + dt) =	( G(f¯	β/2|f, f¯) = f¯	β	2
	G(f¯	+ β/2 f¯, f¯+ β) = f¯+ β
		− |	− 2

w.p. p

(10.52)

w.p. 1 − p.

To maintain uncovered interest parity at the point of intervention, market participants must not expect jumps in the exchange rate. It follows

that, lim∆t→0 Et0 s(t0 +∆t) = st0 . Using (10.52) to evaluate Et0 s(t0 +dt) and equating to s(t0) gives

p	"f¯+ 2 #		+ (1 − p) "f¯−	2 #	= f¯+ B˜(e−λβ − 1),
		β		β

˜

and solving for B gives

B˜ =	(2p − 1)β2	).	(10.53)
	(e−λβ − 1

This solution is a striking contrast to the solution under Krugman

˜

interventions. B is negative if the target zone lacks su cient credibility (p > 12 ). This means that the exchange rate solution is an inverted ‘S- curve’. The exchange rate under the discrete intervention rule combined with low defense credibility is even more volatile than what it would be under a free ßoat.

10.6. IMPERFECT TARGET-ZONE CREDIBILITY

325

Target-zone Summary

1.The theory covered in this chapter was based on the monetary model where today’s exchange rate depends in part on market participant’s expectations of the future exchange rate. Under a target zone, these expectations depend on the position of the exchange rate within the zone. As the exchange rate moves farther away from the central parity, intervention that manipulates the exchange rate becomes increasingly likely and the expectation

of this intervention feeds back into the current value of s(t).

2. When the fundamentals follows a di usion process for f < f < f¯and the target zone is perfectly credible, the exchange rate exhibits mean reversion within the zone. The exchange rate is less responsive to a given change in the fundamentals under a target zone than under a free ßoat. The target zone can be said to have a volatility reducing e ect on the exchange rate.

3.Any target zone–and therefore any Þxed exchange rate regime–operating under a discrete intervention rule will eventually break down because the central bank will ultimately exhaust its foreign exchange reserves. But if the target zone must ultimately collapse, it cannot always be fully credible.

4.When the target zone lacks su cient credibility, the zone itself can be a source of exchange rate volatility in the sense that the exchange rate is even more sensitive to a given change in the fundamentals than it would be under a free ßoat.

326	CHAPTER 10. TARGET-ZONE MODELS