Тема 3. Системы линейных уравнений

В теме рассматриваются вопросы решения систем линейных уравнений методом обратной матрицы и формулы Крамера. Метод Гаусса. Понятие системы линейных однородных уравнений. Фундаментальная система решений.

Определение. Системой линейных алгебраических уравнений называют

или в развернутом виде

(1)

В дальнейшем будем использовать более короткий термин “линейные системы”.

Наиболее компактный вид линейной системы АХ=В, где

А - матрица коэффициентов при неизвестных, которые образуют матрицу-столбец - Х

=(х₁ х₂ ... x_n)^Т,

а свободные члены образуют матрицу-столбец В

=(b₁ b₂... b_m)^T.

Как видим, число уравнений в системе не обязательно равно числу неизвестных. При m=n известен из школьного курса математики метод исключения или метод алгебраического сложения для поиска решения этой системы - матрицы-столбца Х, подстановка которого в каждое уравнение обращает это уравнение в верное равенство (тождество). Однако при наличии большого числа уравнений эти методы становятся неприемлемыми с точки зрения объема вычислений. При этом всегда остается вопрос о наличии того, что мы ищем (есть ли вообще искомое решение), а также о количестве таких решений.

Сначала решим вопрос о поиске гарантированно существующего единственного решения.

3.1.Формулы Крамера

Теорема. Если матрица линейной системы невырождена, то система имеет единственное решение, определяемое по формулам

,

где j - определитель, полученный иззаменой столбца j матрицей-столбцом свободных членов; j=1,2,3,...,m.

Доказательство. Пусть матрица в системе (1) - квадратная размерности . Умножим в системе первое уравнение на А₁₁, 2-е - на А₂₁ и т.д. последнее - на А_m1. Затем суммируем отдельно левые и правые части всех уравнений. Получим после группировки по общим множителям x_j слева x₁(a₁₁A₁₁+a₂₁A₂₁+...+a_m1A_m1)+x₂(a₁₂A₁₁+a₂₂A₂₁+...+a_m2A_m1)+...

+ x_ь(a_1ььA₁₁+a_2ьA₂₁+...+a_mьA_m1) , а справа b₁A₁₁+b₂A₂₁+...+b_mA_m1 .

В первой скобке записан определитель , вычисленный по элементам 1-го столбца. Во 2-й скобке записан нуль по С10, т.к. там записана сумма произведений 2-го столбца на алгебраические дополнения 1-го столбца. Аналогично записана для остальных скобок слева. А справа записано выражение для этого же определителя, первый столбец которого заменен столбцом свободных членов системы. Таким образом получаем равенство. Откуда получаем. Теперь можно повторить весь процесс для алгебраических дополнений 2-го столбца. И получим требуемое утверждение теоремы.

Частный случай - однородная система линейных уравнений

всегда имеет решение Х=(0 0...0)^Т, которое называют тривиальным.

Перейдем к другим возможным ситуациям.

Общий алгоритм решения системы линейных уравнений

Определение. Наибольший из порядков не равных нулю миноров матрицы А называют рангом матрицы и обозначают .

Для поиска ранга используют разные методы. Мы используем метод окаймляющих миноров. Выполним реализацию этого метода на примере.

Пример. Определить ранг матрицы

Решение. Т.к. в матрице есть элементы (“определители” 1-го порядка), не равные нулю, то делаем вывод: . рассмотрим элемент а₁₁=1и записанный в левом верхнем углу матрицы. Если бы там был записан нуль, то всегда можно переставить местами параллельные ряды матрицы так, чтобы на этом месте был записан ненулевой элемент.

Теперь выпишем возможные окаймляющие миноры для элемента а₁₁=1.

Это будут миноры ,,,,,. Фактически - эти миноры поставляют “забор”, который оградил данный элемент “пролетами” из частей рядов матрицы. Легко видеть, что уже первый из них не равен нулю. Т.е.. Значит предстоит его окаймлять, тем более, что он записан в левом верхнем углу. Получаем окаймляющие миноры для минора М₂=.

Это будут и.

Легко подсчитать. что оба они равны нулю. Т.к. других миноров 3-го порядка, окаймляющих минор М₂, нет, то делаем вывод: . При этом М₂ назовем базисным минором матрицы А.

Определение. Матрицу А системы (1) называют основной матрицей системы.

Определение. Если к столбцам основной матрицы приписать справа матрицу-столбец свободных членов, то получится матрица, которую называют расширенная матрица системы.

Так А = 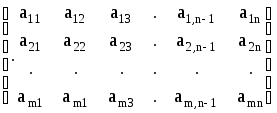основная , а

А₁ = - расширенная матрицы для системы (1).

Теорема Кронекера-Капелли. Для того, чтобы система (1) имела решение (была совместима), необходимо и достаточно, чтобы ранги основной и расширенной матриц были равны. (Без доказательства).

На базе этой теоремы построен алгоритм решения системы линейных уравнений (1) :

1-й шаг - выписываем основную А и расширенную А₁ матрицы системы;

2-й шаг - определяем(находим) ранги и;

3-й шаг - если ранг матрицы А равен рангу матрицы А₁, то переходим к шагу 4, иначе делаем вывод, что система не имеет решения (несовместна);

4-й шаг - выписываем базисный минор;

5-й шаг - отбрасываем уравнения, коэффициенты при неизвестных в которых не вошли в базисный минор;

6-й шаг - неизвестные, чьи коэффициенты не вошли в базисный минор, объявляем свободными (считаем известными величинами) и переносим в столбец свободных членов;

7-й шаг - решаем оставшуюся систему, в которой число уравнений равно числу неизвестных и определителем которой является базисный минор, не равный нулю; Метод решения выбираем по необходимости, т.к. система имеет единственное решение;

8-й шаг - записываем решение исходной системы (1).

Пример 1.5. Решите систему, расширенная матрица которой рассмотрена в примере 4, а основная имеет вид .

Решение. В данном случае пропущены шаги 1,2,3, т.к установлены ранги основной и расширенной матриц. И эти ранги равны.

Поэтому на шаге 4 выписываем готовый базисный минор . Теперь записываем систему, отбросив третье уравнение и положив свободное переменное х₃=С: .

Получаем решение этой системы Х= .

Его принято называть общим, т.к., полагая разные значения С, получим разные решения системы. Теперь запишем решение исходной системы с расширенной матрицей А₁ из примера 4:

Х=.

Ответ: система имеет бесчисленное количество решений, определяемых по формуле для Х.