1.2. Скалярное произведение векторов

Термином (билинейные операции над векторами) иногда называют операции скалярного и векторного произведений двух векторов.

Определение. Скалярным произведением двух векторов иназывают величинуCosф , где ф – угол между векторами. Обозначения или (,).

По этому определению двум векторам ставится в соответствие скаляр, который можно истолковать как работу постоянной по величине и направлению силы на прямолинейном участке пути.

Из определения вытекают простейшие свойства такого произведения.

1. =;

2. С()=(С).

3. (+)=+

4. =0

для ненулевых векторов, если векторы ортогональны (перпендикулярны).

Можно получить формулу для вычисления скалярного произведения,

если векторы заданы в координатной форме (своими координатами). Пусть =a_x+a_y+a_z и =b_x+b_y+b_z. Тогда =a_x b_x +a_y b_y +a_z b_z. Т.к. при перемножении по свойству 3 с учетом определения остальные слагаемые будут равны нулю.

Из последнего соотношения следует, что =² .Читается – скалярный квадрат равен квадрату модуля.

Из определения и полученных соотношений вытекают другие формулы. Например, для проекции одного вектора на другой получаем =. Условие перпендикулярности векторовa_xb_x+a_yb_y+a_zb_z=0.

1.3. Векторное произведение векторов

Определение. Векторным произведением двух векторов иназывают вектор, который:

-имеет модуль, равный произведению модулей перемножаемых векторов на синус угла меду ними - =sinф;

-ортогонален (перпендикулярен) каждому из векторов и(т.е. плоскости с векторамии);

-вместе с векторами ив порядке,,образует правую тройку векторов. Обозначают векторное произведениеили [,].

Классическое понятие правой тройки векторов ,,в указанном порядке: если наблюдать с конца любого вектора поворот от следующего за ним к предыдущему в направлении против часовой стрелки, то тройка векторов правая. В противном случае – левая.

Примером правой тройки будет набор декартовых базисных векторов ,,. А в бытовом понятии правую тройку связывают с правым буравчиком (правой резьбой), когда при вращении по часовой стрелке буравчик (винт, гайка) продвигается вглубь от вращающего.

Т.к. sinф, то геометрически определение говорит о том, что площадь параллелограмма, построенного на множителях иравна модулю вектора.

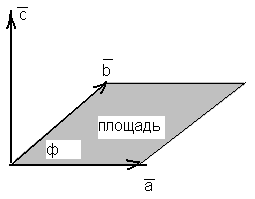
К определению

В качестве механической интерпретации векторного произведения может быть взят момент силы(постоянной по величине и направлению), приложенной к точке А относительно точки О. Векторнаправлен так, что образует правую тройку с перемножаемыми векторами и численно равен величинеSinф.

Механическая интерпретация .

Справедливы следующие свойства векторного произведения.

С1.Для коллинеарных векторов исправедливо=0.

С2. =.

С3. =).

Координатная форма вычисления . Пусть =a_x+a_y+a_z и =b_x+b_y+b_z. Тогда =(a_x+a_y+a_z)х(b_x+b_y+b_z). Далее используем взаимное расположение векторов,,и свойство 3 получим по определению

a_xb_xх+a_yb_xх+a_zb_xх+a_хb_ух+a_уb_yх+a_zb_ух+ +a_xb_zх+a_y b_z х+a_z b_zх= (a_хb_у-a_yb_x)+(a_zb_x- a_xb_z)+

+( a_y b_z - a_zb_у) =. Полученная символическая формула не противоречит ни свойствам определителя о смене знака при смене местами параллельных рядов, ни свойству векторного произведения о смене знака при смене порядка множителей. Из нее получается простое правило проверки коллинеарности векторов – равенство отношений (или пропорциональность координат).

Смешанное произведение векторов

Рассмотрим произведения трех векторов :

((,),) – уже известное нам произведение скаляра на вектор – и потому ничего нового;

[[,],] - двойное векторное произведение, которое имеет узкое приложение в механике;

([,],) – векторно-скалярное (смешанное) произведение, которое имеет широкое применение в математике и приложениях.

Анализируя известное произведение [,] по Рис.2.2, можно получить геометрическую интерпретацию для смешанного произведения

([,],). Модуль векторного произведения – площадь параллелограмма, построенного на векторах-множителях и равной=. Если теперь перемножить скалярно векторы и, то получим отрезок ОВ, равный высоте параллелепипеда, построенного на векторах-сомножителях,,как на ребрах. Т.о., модуль ([,],) численно равен объему параллелепипеда, построенного на векторах множителях.

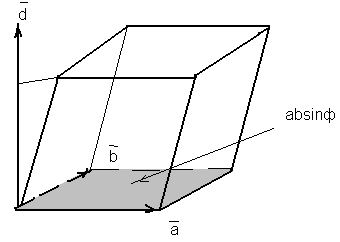
К определению ([,],)

Используя координатную форму векторного произведения, получаем координатную форму смешанного произведения

([,],)= ( с_x+с_y+с_z)=((a_хb_у - a_yb_x )+(a_zb_x- a_xb_z)+(a_y b_z - a_zb_у) ) ) ( с_x+с_y+с_z)=(a_хb_у - a_yb_x ) с_x +( a_zb_x- a_xb_z) с_y +( a_y b_z - a_zb_у) с_z = =.

Если в последнем определителе переставим местами 1-ю и 3-ю строки, то определитель не изменится и мы получим более удобную запись координат перемножаемых векторов в порядке их следования в произведении.

Из последней формулы для вычисления смешанного произведения следует возможность проверки компланарности (параллельности одной плоскости) трех векторов – если ([,],)=0, то векторы-множители компланарны. И следствием последнего равенства будет условие линейной зависимости трех векторов в пространстве.