4.7. Уравнения 2-й степени в пространстве

Определение. Уравнением второго порядка в пространстве (уравнением поверхности 2-го порядка) называют уравнение вида

a₁₁x²+a₂₂y²+a₃₃z²+2a₁₂xy+2a₁₃xz+2a₂₃yz+a₄₁x+a₄₂y+a₄₃z+ a₄₄=0 (7.1)

Мы познакомимся только с уравнением (6.3), в котором отсутствуют произведения текущих координат. В этом случае имеется возможность выделить полные квадраты по переменным и получить уравнение поверхности в каноническом виде. Последние и будем изучать более подробно.

Для исследования канонических уравнений поверхностей второго порядка используют метод сечений. В самом простом виде он выглядит так: проводят серии плоскостей, параллельных координатным плоскостям и по результатам (виду сечений) делают вывод о форме поверхности. Эта работа похожа на работу томографа при исследовании внутренних органов человека в медлабораториях или работу топографа при топографической съемке местности.

Реализуем метод при построении поверхности ++=1

Рассечем поверхность плоскостями z=h. Тогда в сечении получим

,

Из этой системы видно, что h не может превышать z=hс. Что означает – поверхность расположена между двумя плоскостями – выше h=-c и ниже h=c. Более того, в сечениях получаются эллипсы, самый большой из которых расположен в плоскости z=0. Чем дальше от плоскости хОу, тем меньше эллипс. И на высоте с эллипс вырождается в точку.

Если провести аналогичные серии плоскостей . параллельных другим координатным плоскостям, то получим похожие выводы. Следовательно, поверхность образована скольжением эллипсов по эллипса и называется трехосным эллипсоидом.

4.8. Цилиндры и поверхности вращения

Из поверхностей, отличных от 2-го порядка рассмотрим два частных случая.

Пусть задано уравнение F(x;y)=0 в пространстве. И требуется установить, как выглядит поверхность.

Комментарий. Т.к. сказано, что уравнение задано в пространстве, то отсутствие в уравнении некоторых переменных не противоречит определению поверхности в пункте 6.1.

Рассуждаем так. Добавим к этому уравнению уравнение z=0. Тогда

Эта система есть линия на плоскости хОу. На ней можно взять точку М(х;у). Если теперь эту точку перемещать вдоль Oz, не меняя х и у этой точки, то уравнение поверхности F(x;y)=0 будет тождественно выполняться, т.к. тождественно выполняется первое уравнение системы. Значит поверхность образована движением прямой, параллельной Oz и пересекающей данную линию на плоскости. Естественно эту поверхность назвать цилиндрической. У нее две характеристики, определяющие ее вид : кривая F(x;y)=0 при z=0 – направляющая цилиндра; и прямая, пересекающая эту кривую, перпендикулярная плоскости расположения кривой и называемая образующей цилиндра.

Вывод: всякое уравнение с двумя переменными в пространстве определяет цилиндрическую поверхность с образующей, параллельной отсутствующей координате и направляющей – кривой в плоскости переменных, записанных в уравнении поверхности.

Пусть дана плоская линия для определенности в плоскости хОу уравнениями

На ней можно взять точку М(х;у). Если теперь эту точку вращать около оси Oх, то точка опишет окружность с центром на оси Ох и радиусом, равным у точки М. Уравнение этой окружности Z2+Y2=y2 . В уравнении большими буквами записаны фактически меняющиеся координаты точки на окружности, а малое у – это радиус. Такие же окружности описывают все точки кривой и образуется поверхность вращения. На каждой окружности этой поверхности х=Х. Если из уравнения окружности выразить у и подставить в уравнение кривой, то получим F(Х,)=0. Но последнее уравнение содержит три переменные и потому является уравнением поверхности вращения взятой в начале линии относительно Ох.

Вывод: если в некотором уравнении квадраты двух переменных имеют одинаковые коэффициенты, то это поверхность вращения. А механизм получения уравнения поверхности , образованной вращением некоторой линии относительно координатной оси, представлен выше.

Контрольные вопросы и задания для самостоятельной подготовки:

1. Уравнение прямой на плоскости. Общее уравнение.

2. Уравнение прямой на плоскости. Уравнение линии в отрезках.

3. Уравнение прямой на плоскости. Уравнение с угловым коэффициентом.

4. Линии второго порядка. Эллипс.

5. Линии второго порядка. Парабола.

6. Линии второго порядка. Гипербола.

7. Прямая и плоскость в пространстве.

8. Даны три вектора: Составить Уравнение прямой, проходящей через точкуА(5;-1) под углом к осиОх.

9. Составить уравнение плоскости, проходящей через точку М(1;-2;3) и перпендикулярной вектору;

10. Составить уравнение плоскости, проходящей через точку М(1;-2;3) и параллельно плоскости 3х-4у+5z+6=0;

11. Составить уравнение плоскости, проходящей через точку М(1;-2;3) и точку и параллельной осиОу;

12. Составить уравнение плоскости, проходящей через точку М(1;-2;3) и проходящей через ось Оz.

13. Составить уравнение плоскости, проходящей через прямуюи точкуМ(2;0;1)

14. Составить уравнение плоскости, проходящей через две параллельные прямые

15. В треугольнике АВС даны уравнения: стороны АВ 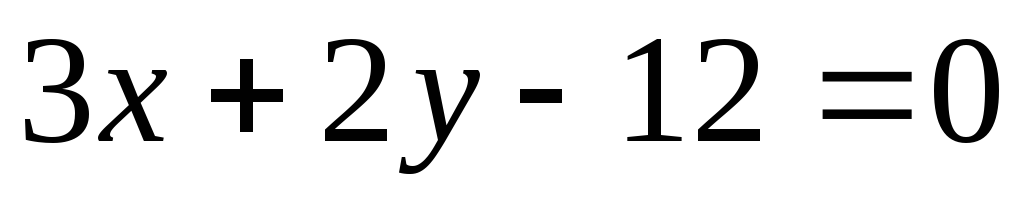, высоты ВМ ,высоты АМ ,где точка М – точка пересечения высот. Найти уравнения сторон АС, ВС и стороны СМ.

16. Две стороны параллелограмма заданы уравнениями и. Диагонали его пересекаются в начале координат. Найти уравнения сторон параллелограмма и его диагоналей.

17. Ординаты все точек окружности сокращены втрое. Написать уравнение полученной новой кривой.

18. Эллипс, симметричный относительно осей координат, проходит через точки и. Найти полуоси, координаты фокусов и эксцентриситет эллипса.

19. Для гиперболы найти действительную и мнимую полуоси; координаты фокусов; эксцентриситет; уравнения асимптот.

20. Составить уравнения параболы, проходящей через точки исимметрично относительно оси Ох.