3.3.Матричный метод решения линейной системы.

Определение. Матрицу А^-1 называют обратной для матрицы А, если А^-1 А=А А^-1 =Е.

Из определения следует, что матрицы А и А^-1 квадратные и для них справедлив переместительный закон.

Теорема. Если А невырождена, то обратная матрица существует.

Доказательство. Ограничимся квадратной матрицей 2-го порядка.

Пусть имеется некоторая матрица А=.

Пусть detA0. Пусть имеется некоторая матрица В=- неизвестная нам. И пусть АВ=Е , где Е=. Тогда после умножения слева по равенству матриц получаем систему 4-х уравнений с четырьмя неизвестными элементами матрицы В :, которая фактически распадается на две автономные системы, каждая из которых имеет один и тот же определитель, равныйопределителю матрицы А и только по две переменные.:Каждую из этих систем можно решить, например, по формулам Крамера и получить ответ в виде:в числителях каждой дроби записано алгебраическое дополнение соответствующих элементов транспонированной матрицы А^Т. Доказательство закончено. И из него вытекает алгоритм поиска А^-1 :

1-й шаг - вычисли detA;

2-й шаг - если detA не равен нулю, перейдите к пункту 3, иначе обратной матрицы не существует;

3-й шаг - транспонируйте матрицу А;

4-й шаг - для всех элементов транспонированной матрицы выпишите алгебраические дополнения;

5-й шаг составьте обратную матрицу из отношений .

Используя обратную матрицу легко решить линейную систему, если она имеет единственное решение. В самом деле, пусть дана система АХ=В с невырожденной матрицей А (т.е. detA0). Сформируем матрицу А^-1 по вышеприведенному алгоритму. Теперь умножим слева обе части уравнение АХ=В на матрицу А^-1. Получим А^-1АХ= А^-1 В. Но А^-1 А=Е, а ЕХ=Х и потому получаем Х= А^-1В.

Пример 1.6. Решите систему

Ранг основной и расширенной матрицы этой системы равен 2 и потому система имеет решение. Базисный минор системы равен М₂ и приведен в примере 5. Фактически нам предстоит решить систему .

На этот раз мы решим ее, используя обратную матрицу для последней системы. Так как матрица последней системы невырождена (detA= М₂), легко найти ее обратную матрицу А^-1 =, а потому решение принимает вид Х==.

А для исходной системы Х=.

Ответ: система имеет бесчисленное количество решений, определяемых по формуле для Х.

3.4. Понятие о приближенных методах решения линейных систем

Рассмотренные примеры решения линейных систем являются чисто учебными. На практике (при решении прикладных профессиональных или научных задач) приходится решать системы с сотнями , тысячами и даже сотнями тысяч уравнений. Естественно, что выполнить это можно только специальными численными методами. Понятие о некоторых из них и рассматривается в этом разделе. Сразу следует отметить, что эти методы обеспечивают поиск только единственно существующего решения системы. Вопросы обеспечения наличия или отсутствия решения решает тот, кто собирается решать такую систему.

Для линейных систем с несколькими сотнями уравнений используют метод Гаусса (метод последовательного исключения неизвестных в разных вариациях). Для систем с несколькими тысячами уравнений, матрицы которых имеют специальный вид, используют итерационные методы решения(о которых будет сказано ниже). Для большего числа уравнений используют вероятностные методы Монте-Карло).

Пусть систему АХ+В удалось преобразовать к виду Х= А₁Х+В₁. Если матрица А₁ такова, что:

- сумма модулей коэффициентов строки (для всех строк) не превосходит 1;

- сумма модулей коэффициентов столбца (для всех столбцов) не превосходит 1, тогда можно организовать вычислительный процесс по схеме Х^(k+1)= А₁Х^(k) +В₁, где k - номер предыдущего приближения к решению системы. Этот процесс называют итерационным (повторяющимся) и продолжают до тех пор, пока , где- требуемая погрешность решения задачи. В качестве приближенного решения системы берут матрицу-столбец Х^(k+1) .

Пример 1.7. Методом итераций решить систему

Решение. переставим в системе первое и второе уравнение. Затем из первого уравнения найдем х₁; из второго - х₂ и из третьего х₃. В результате получим систему вида

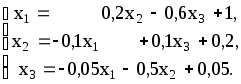
Теперь организуем итерационный процесс по схеме

Проверяем выполнение условий сходимости процесса к точному решению системы. Видим ,что сумма модулей коэффициентов при неизвестных в 1-й строке равна 0,8 , что меньше 1. То же самое верно для

2-й и 3-й строк. Т.о. система обеспечивает сходимость приближений к точному решению.

В эту итерационную схему в качестве нулевого (k=0) приближения в правую часть подставим столбец свободных членов (так чаще всего и делают, хотя можно было брать любой набор для неизвестных)

Х^(о) = (1 0,2 0,05) ^Т .Тогда после вычислений справа получим слева первое (k=1) приближение Х⁽¹⁾ = (1,01 0,105 -0,1) ^Т. Повторим вычисления и получим последовательно Х⁽²⁾ = (1,081 0,089 -0,053) ^Т ;

Х⁽³⁾ = (1,050 0,087 -0,048) ^Т ; Х⁽⁴⁾ = (1,046 0,090 -0,046) ^Т;

Х⁽⁵⁾ = (1,046 0,090 -0,047) ^Т; Х⁽⁶⁾ = (1,046 0,090 -0,048) ^Т. Мы видим, Что между 6-м и 5-м приближениями расхождение не превосходит 0,001. Поэтому в качестве решения системы может быть принято шестое приближение Х= Х⁽⁶⁾ = (1,046 0,090 -0,048) ^Т .Это значит : х₁=1,046; х₂=0,090; х₃=-0,046.

Контрольные вопросы и задания для самостоятельной подготовки:

1. Общий вид и свойства системы уравнений.

2. Матричная форма системы уравнений.

3. Методы решения систем линейных уравнений. Метод обратной матрицы.

4. Методы решения систем линейных уравнений. Метод Крамера.

5. Методы решения систем линейных уравнений. Метод Гаусса.

6. Вычисление обратной матрицы методом Гаусса.

7. Системы однородных линейных уравнений, их решение.

8. Фундаментальная система решений.

9. Решить систему линейных уравнений методом Крамера:

10. Методом Гаусса решить систему:

11. Решить систему линейных уравнений методом Крамера:

12. Решить систему линейных уравнений методом Гаусса:

13. Решить систему линейных уравнений методом Крамера:

14. Решить систему линейных уравнений методом Гаусса:

15. Решить систему линейных уравнений методом Крамера:

16. Решить систему линейных уравнений методом Гаусса:

17. Решить систему линейных уравнений методом Крамера:

18. Решить систему линейных уравнений методом Гаусса: