
- •Лекционный курс
- •Раздел 1. Линейная алгебра с элементами аналитической геометрии
- •Тема 1. Элементы векторной алгебры и ее приложения.
- •1.1. Линейные операции над векторами
- •1.2. Скалярное произведение векторов
- •1.3. Векторное произведение векторов
- •1.4. Типовые задачи, решаемые средствами векторной алгебры
- •1.5. Линейное, евклидово и нормированное пространства.
- •Тема 2. Матрицы и определители
- •2.1. Понятие матрицы и действия с ними.
- •2.2. Транспонирование матриц
- •2.3. Произведение матриц.
- •2.4. Ранг матрицы
- •2.5. Понятие обратной матрицы
- •2.6.Определители и их свойства.
- •2.7. Линейные операторы и матрицы
- •2.8. Задача о собственных значениях
- •2.9. Свойства симметрических матриц
- •2.10. Квадратичные формы и их приведение к каноническому виду
- •Тема 3. Системы линейных уравнений
- •3.1.Формулы Крамера
- •3.2. Метод Гаусса.
- •3.3.Матричный метод решения линейной системы.
- •3.4. Понятие о приближенных методах решения линейных систем
- •Тема 4. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.
- •4.1. Уравнения линий и поверхностей
- •4.2. Уравнение 1-й степени на плоскости
- •4.3. Уравнения первой степени в пространстве
- •4.4. Уравнения первой степени в пространстве
- •4.5. Типовые задачи на плоскость в пространстве.
- •4.6. Уравнения 2-й степени на плоскости.
- •4.7. Уравнения 2-й степени в пространстве
- •4.8. Цилиндры и поверхности вращения
- •Раздел 2. Математический анализ и дифференциальные уравнения.
- •Тема 5.Функции и их свойства
- •5.1. Функция, способы ее задания, свойства, график функции, преобразование графика сдвигом и деформацией.
- •Тема 6. Пределы и непрерывность.
- •6.1. Понятие предела
- •6.2. Замечательные пределы.
- •6.3. Алгоритм вычисления пределов.
- •6.4. Примеры эквивалентных бмв.
- •Тема 7. Производная и дифференциал функции.
- •7.1. Понятие производной
- •7.2. Дифференциальное исчисление функции одного переменного.
- •7.3. Из определения вытекает алгоритм вычисления производной.
- •7.4.Таблица и основные правила.
- •7.5. Производная и дифференциал.
- •7.6. Производная и дифференциал высшего порядка.
- •Тема 8. Приложения производной
- •8.2.Приложение производной к исследованию функций.
- •Тема 9. Неопределенный интеграл.
- •9.1.Первообразная. Неопределенный интеграл и его свойства
- •9.3.Методы интегрирования.
- •9.4.Рациональные дроби.
- •9.4.Рациональные тригонометрические функции.
- •9.5.Простейшие иррациональные выражения.
- •Тема 10. Определенный интеграл.
- •Методы нахождения определенного интеграла
- •10. 2.Несобственные интегралы.
- •Тема 11. Дифференциальные уравнения.
- •11.1 Определение дифференциального уравнения
- •11.2. Некоторые дифференциальные уравнения первого порядка. Методы Их Решения.
- •Тема 12 Функции нескольких переменных
- •12.1.Основные понятия
- •12.2.Непрерывность функций нескольких переменных
- •12.3.Частные производные и дифференциалы
- •12.4. Производная по направлению и градиент
- •12.5. Производная сложной функции нескольких переменных
- •12.6. Производные и дифференциалы высших порядков
- •12.7. Производные неявных функций
- •12.8.Экстремумы функций нескольких переменных
- •Раздел 3. Ряды.
- •Тема 13. Числовые и степенные ряды.
- •Раздел 4. Теория вероятностей и математическая статистика
- •Тема 14. Основные понятия теории вероятностей.
- •1. Понятие события.
- •2. Классическое определение вероятности. Свойства вероятности.
- •3. Статистическое определение вероятности.
- •4. Элементы комбинаторики
- •Тема 15. Основные теоремы теории вероятностей и следствия из них.
- •15.1.Теорема сложения.
- •15.2. Условная вероятность события. Теорема умножения
- •15.3. Вероятность появления хотя бы одного события
- •15.4. Формула полной вероятности.Формула Байеса.
- •15.5. Повторные независимые испытания
- •15.6. Локальная теорема Муавра- Лапласа
- •15.7. Интегральная теорема Муавра-Лапласа.
- •Тема 16. Случайные величины и способы их описания
- •16.1. Понятие случайной величины. Дискретные и непрерывные
- •16.2. Функция распределения случайной величины. График функции
- •16.4. Равномерный закон распределения.
- •16.6. Правило «трех сигм».
- •16.7. Показательное распределение.
- •16.8. Функция надежности.
- •16.9. Показательный закон надежности.
- •16.10. Математическое ожидание.
- •16.11. Дисперсия.
- •16.12. Числовые характеристики непрерывных случайных величин.
- •16.13. Числовые характеристики случайных величин, имеющих некоторые стандартные законы распределения.
- •1. Биномиальное распределение.
- •2. Закон Пуассона.
- •3. Равномерное распределение.
- •4. Нормальное распределение.
- •16.14. Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли.
- •Корреляционный анализ.
- •Глоссарий
- •Темы контрольных работ.
- •Основная литература
- •Дополнительная литература
7.4.Таблица и основные правила.
Применяя алгоритм, легко получить такие правила поиска производных:
(с)’=0
; x’=1;
(u(x)
![]() v(x))’=(
u(x))’
v(x))’=(
u(x))’
![]() (v(x))’.
(v(x))’.
Сложнее
получить формулу (u(x)v(x))’=u’(x)v(x)+u(x)v(x).
Получим ее, несколько сократив запись
алгоритма. Получаем f(x)=
u(x)v(x).
Тогда f(x+![]() )=
u(x+
)=
u(x+![]() )v(x+
)v(x+![]() ).
Но лучше это записать так f(x+
).
Но лучше это записать так f(x+![]() )=
(u(x)+
)=
(u(x)+![]() )(v(x)+
)(v(x)+![]() ),
потому что при изменении переменной х
изменяются и переменные u
и v.
Далее получаем f(x+
),
потому что при изменении переменной х
изменяются и переменные u
и v.
Далее получаем f(x+![]() )-
f(x)==
(u(x)+
)-
f(x)==
(u(x)+![]() )(v(x)+
)(v(x)+![]() )--u(x)v(x)=
v(x)
)--u(x)v(x)=
v(x)
![]() +u(x)
+u(x)
![]() .
Разделим полученное на
.
Разделим полученное на
![]() и вычислим предел отношения. Получим
рабочую формулу.
и вычислим предел отношения. Получим
рабочую формулу.
По
аналогичной схеме можно получить
производную частного
![]() =
=![]() .
Для доказательства достаточно записатьf(x+
.
Для доказательства достаточно записатьf(x+![]() )=
)=![]() в виде f(x+
в виде f(x+![]() )=
)=![]() и далее продолжить алгоритм вычисления
производной
и далее продолжить алгоритм вычисления
производной
![]() =
= =
=
 =
= =
=![]() .
.
Если
y=f(x)
и х=ф(у) взаимно обратные функции, то их
производные связаны соотношением y’x=![]() .
Доказательство следует из
.
Доказательство следует из
![]() =
=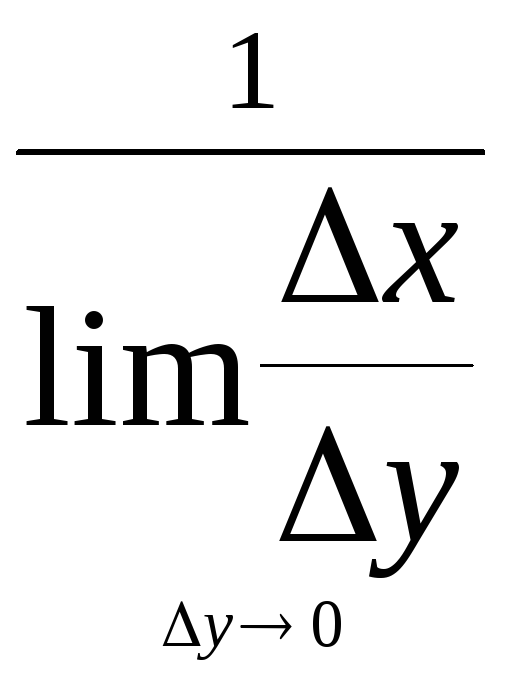
Если y=f(x) и х=ф(t) (т.е. y=f(ф(t)) – сложная функция), то y’t= y’xx’t , где y’x= f’x(x) , а x’t = ф’t(t).
Доказательство
следует из цепочки преобразований
![]() =
=![]()
![]() и затем вычислить предел полученного
при
и затем вычислить предел полученного
при
![]()
![]() 0,
что приведет к тому что
0,
что приведет к тому что
![]()
![]() 0.
0.
Бывают
ситуации, когда функция y=f(x)
задана параметрически, т.е. в виде
![]() .
Тогда используют тот факт, что отношение
.
Тогда используют тот факт, что отношение
![]() всегда можно преобразовать по схеме
всегда можно преобразовать по схеме
![]() .
А при вычислении производной получить
в ответе запись y’=
.
А при вычислении производной получить
в ответе запись y’=![]() .
.
Используя эти правила, получаем сначала таблицу производных основных элементарных функций.

Функция Ее производная Вывод формулы и комментарии

y=ax
, a![]() 1,a>0;
y’= ax
lna; Имеем
y+
1,a>0;
y’= ax
lna; Имеем
y+![]() =
ax+
=
ax+![]() ,
,
![]() =ax+
=ax+![]() -ax
= ax
(a
-ax
= ax
(a![]() -1)
-1)
Теперь
 =
= =
=
=
ax
![]() =ax
lna.
=ax
lna.
y=ex , y’= ex ; Как частный случай для предыдущей
формулы.
y=lnx
y’=![]() ;
Т.к. х=eу
, то на основании связи производных
;
Т.к. х=eу
, то на основании связи производных
взаимно обратных функций имеем
(lnx)’x= ==
==![]() =
=![]() .
.
y=х , y’=х , Имеем y=х = elnx . Далее используем
предыдущую формулу и производную от
сложной
функции
y’=
elnx
![]() =х
.
=х
.
y=Sinx
y’=Cosx Имеем
![]() =Sin(x+
=Sin(x+![]() )-Sinx=2Cos
)-Sinx=2Cos![]() Sin
Sin![]() ;
;
теперь
y’=
![]()
![]() =
=
![]()
![]() =Cosx.
=Cosx.
y=Cosx
y’=-Sinx В
самом
деле
(Cosx)’=(sin(![]() -x))’=
-x))’=
Cos(![]() -x)(-x)’=-Sinx.Применена
формула
-x)(-x)’=-Sinx.Применена
формула
Приведения и производная сложной
функции.
y=tgx
y’=![]() Достаточно записать производную
от дроби
Достаточно записать производную
от дроби
(tgx)’=![]() далее преобразовать рез-т.
далее преобразовать рез-т.
y=arcSinx
y’=![]() В самом деле, по условию x=Siny.
Для
В самом деле, по условию x=Siny.
Для
взаимно обратных функций имеем (arcSinx)’=
=![]() =
=![]() =
=![]() =
=![]() .
.
y=arctgx
y’=![]() Схему получения смотри выше.
Схему получения смотри выше.
y=arcCosx
y’=-![]() Ввиду того, что arcCosx=
Ввиду того, что arcCosx=![]() -arcSinx.
-arcSinx.
y=arcctgx
y’=-![]() Схему получения смотри выше.
Схему получения смотри выше.
В
тех случаях, когда применить вышеприведенные
правила и таблицу затруднительно, можно
использовать прием, называемый
логарифмическим дифференцированием .
Пусть мы имеем y=![]() .
Тогда невозможно применить ни одну их
записанных выше формул. Поступают так.
Сначала логарифмируем обе части равенства
и получаем lny=ф(х)ln(f(x)).
Теперь возьмем производную от каждой
части равенства, зная, что у – это функция
от х. Получаем
.
Тогда невозможно применить ни одну их
записанных выше формул. Поступают так.
Сначала логарифмируем обе части равенства
и получаем lny=ф(х)ln(f(x)).
Теперь возьмем производную от каждой
части равенства, зная, что у – это функция
от х. Получаем
![]() y’=ф’(x)lnf(x)+ф(x)
y’=ф’(x)lnf(x)+ф(x)
![]() f’(x).
Из полученного равенства найдем
требуемое
f’(x).
Из полученного равенства найдем
требуемое
y’=y(ф’(x)ln(f(x))+ф(x)
![]() f’(x))=
f’(x))=![]() (ф’(x)ln(f(x))+ф(x)
(ф’(x)ln(f(x))+ф(x)
![]() f’(x)).
f’(x)).
Возможен
и другой подход. Имеем y=![]() =
=![]() .
После чего можно искать производную по
правилу сложной функции. Получаем
.
После чего можно искать производную по
правилу сложной функции. Получаем
y’=![]() (
ф’(x)lnf(x)+ф(x)
(
ф’(x)lnf(x)+ф(x)
![]() f’(x))=
f’(x))=
![]() (ф’(x)ln(f(x))+ф(x)
(ф’(x)ln(f(x))+ф(x)
![]() f’(x)).
f’(x)).
Если же функция y=f(x) задана неявно, т.е. уравнением F(x;y)=0, то для поиска производной следует взять производную от равенства F(x;y)=0, зная, что у= f(x), хотя f(x) и неизвестна. Затем из полученного равенства находят y’.
