
- •Лекционный курс
- •Раздел 1. Линейная алгебра с элементами аналитической геометрии
- •Тема 1. Элементы векторной алгебры и ее приложения.
- •1.1. Линейные операции над векторами
- •1.2. Скалярное произведение векторов
- •1.3. Векторное произведение векторов
- •1.4. Типовые задачи, решаемые средствами векторной алгебры
- •1.5. Линейное, евклидово и нормированное пространства.
- •Тема 2. Матрицы и определители
- •2.1. Понятие матрицы и действия с ними.
- •2.2. Транспонирование матриц
- •2.3. Произведение матриц.
- •2.4. Ранг матрицы
- •2.5. Понятие обратной матрицы
- •2.6.Определители и их свойства.
- •2.7. Линейные операторы и матрицы
- •2.8. Задача о собственных значениях
- •2.9. Свойства симметрических матриц
- •2.10. Квадратичные формы и их приведение к каноническому виду
- •Тема 3. Системы линейных уравнений
- •3.1.Формулы Крамера
- •3.2. Метод Гаусса.
- •3.3.Матричный метод решения линейной системы.
- •3.4. Понятие о приближенных методах решения линейных систем
- •Тема 4. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.
- •4.1. Уравнения линий и поверхностей
- •4.2. Уравнение 1-й степени на плоскости
- •4.3. Уравнения первой степени в пространстве
- •4.4. Уравнения первой степени в пространстве
- •4.5. Типовые задачи на плоскость в пространстве.
- •4.6. Уравнения 2-й степени на плоскости.
- •4.7. Уравнения 2-й степени в пространстве
- •4.8. Цилиндры и поверхности вращения
- •Раздел 2. Математический анализ и дифференциальные уравнения.
- •Тема 5.Функции и их свойства
- •5.1. Функция, способы ее задания, свойства, график функции, преобразование графика сдвигом и деформацией.
- •Тема 6. Пределы и непрерывность.
- •6.1. Понятие предела
- •6.2. Замечательные пределы.
- •6.3. Алгоритм вычисления пределов.
- •6.4. Примеры эквивалентных бмв.
- •Тема 7. Производная и дифференциал функции.
- •7.1. Понятие производной
- •7.2. Дифференциальное исчисление функции одного переменного.
- •7.3. Из определения вытекает алгоритм вычисления производной.
- •7.4.Таблица и основные правила.
- •7.5. Производная и дифференциал.
- •7.6. Производная и дифференциал высшего порядка.
- •Тема 8. Приложения производной
- •8.2.Приложение производной к исследованию функций.
- •Тема 9. Неопределенный интеграл.
- •9.1.Первообразная. Неопределенный интеграл и его свойства
- •9.3.Методы интегрирования.
- •9.4.Рациональные дроби.
- •9.4.Рациональные тригонометрические функции.
- •9.5.Простейшие иррациональные выражения.
- •Тема 10. Определенный интеграл.
- •Методы нахождения определенного интеграла
- •10. 2.Несобственные интегралы.
- •Тема 11. Дифференциальные уравнения.
- •11.1 Определение дифференциального уравнения
- •11.2. Некоторые дифференциальные уравнения первого порядка. Методы Их Решения.
- •Тема 12 Функции нескольких переменных
- •12.1.Основные понятия
- •12.2.Непрерывность функций нескольких переменных
- •12.3.Частные производные и дифференциалы
- •12.4. Производная по направлению и градиент
- •12.5. Производная сложной функции нескольких переменных
- •12.6. Производные и дифференциалы высших порядков
- •12.7. Производные неявных функций
- •12.8.Экстремумы функций нескольких переменных
- •Раздел 3. Ряды.
- •Тема 13. Числовые и степенные ряды.
- •Раздел 4. Теория вероятностей и математическая статистика
- •Тема 14. Основные понятия теории вероятностей.
- •1. Понятие события.
- •2. Классическое определение вероятности. Свойства вероятности.
- •3. Статистическое определение вероятности.
- •4. Элементы комбинаторики
- •Тема 15. Основные теоремы теории вероятностей и следствия из них.
- •15.1.Теорема сложения.
- •15.2. Условная вероятность события. Теорема умножения
- •15.3. Вероятность появления хотя бы одного события
- •15.4. Формула полной вероятности.Формула Байеса.
- •15.5. Повторные независимые испытания
- •15.6. Локальная теорема Муавра- Лапласа
- •15.7. Интегральная теорема Муавра-Лапласа.
- •Тема 16. Случайные величины и способы их описания
- •16.1. Понятие случайной величины. Дискретные и непрерывные
- •16.2. Функция распределения случайной величины. График функции
- •16.4. Равномерный закон распределения.
- •16.6. Правило «трех сигм».
- •16.7. Показательное распределение.
- •16.8. Функция надежности.
- •16.9. Показательный закон надежности.
- •16.10. Математическое ожидание.
- •16.11. Дисперсия.
- •16.12. Числовые характеристики непрерывных случайных величин.
- •16.13. Числовые характеристики случайных величин, имеющих некоторые стандартные законы распределения.
- •1. Биномиальное распределение.
- •2. Закон Пуассона.
- •3. Равномерное распределение.
- •4. Нормальное распределение.
- •16.14. Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли.
- •Корреляционный анализ.
- •Глоссарий
- •Темы контрольных работ.
- •Основная литература
- •Дополнительная литература
Тема 10. Определенный интеграл.
Дается понятие определенного интеграла, его геометрический и экономический смысл. Свойства определенного интеграла. Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница. Замена переменной и формула интегрирования по частям в определенном интеграле. Геометрические приложения определенного интеграла. Несобственные интегралы. Приближенное вычисление определенных интегралов. Использование определенного интеграла в экономике.
Пусть
на [a;b]
задана f(x).
Разобьем
отрезок на n
частей точками. На каждой части выберем
точку Мк. Вычислим сумму
![]() и назовем ее интегральной. Таких сумм
можно составить сколько угодно (изменяя
способ разбиения и выбор токи Мк на
каждом участке разбиения). Вычислим
предел интегральной суммы приn
и назовем ее интегральной. Таких сумм
можно составить сколько угодно (изменяя
способ разбиения и выбор токи Мк на
каждом участке разбиения). Вычислим
предел интегральной суммы приn![]() и максимальном
и максимальном
![]() 0
0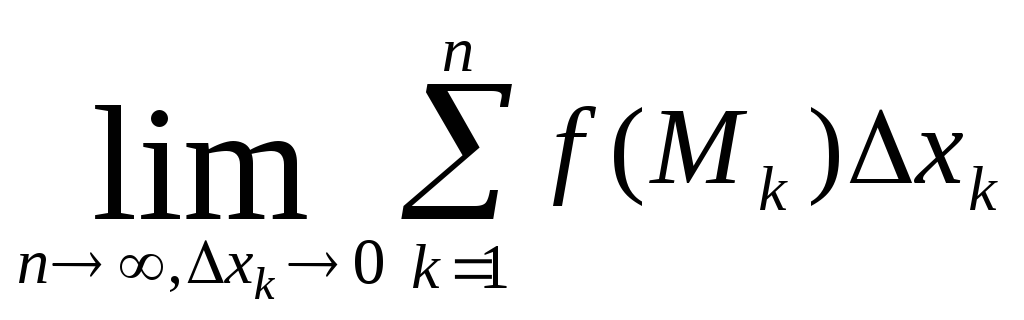 .
Если указанный предел существует
независимо от способа разбиения [a;b]
на части и выбора
.
Если указанный предел существует
независимо от способа разбиения [a;b]
на части и выбора
![]()
![]() на каждом участке разбиения, а только
в зависимости отf(x)
и длины отрезка [a;b],
то такой предел назовем определенным
интегралом и обозначим
на каждом участке разбиения, а только
в зависимости отf(x)
и длины отрезка [a;b],
то такой предел назовем определенным
интегралом и обозначим
![]() .
В этом определении : - символ определенного
интеграла; f(x)
– подынтегральная функция; а – нижний
предел интегрирования; b
– верхний предел интегрирования; х (под
знаком d)
– аргумент интегрирования.
.
В этом определении : - символ определенного
интеграла; f(x)
– подынтегральная функция; а – нижний
предел интегрирования; b
– верхний предел интегрирования; х (под
знаком d)
– аргумент интегрирования.
Теорема существования. Если f(x) ограничена на [a;b] и непрерывна на нем всюду кроме конечного числа точек разрыва 1-го рода, то определенный интеграл существует.
Основные свойства ОИ.
![]()
![]() .
Док. Следует из свойства предела.
.
Док. Следует из свойства предела.
![]() .
Достаточно в качестве одной из точек
разбиения выбрать точку С.
.
Достаточно в качестве одной из точек
разбиения выбрать точку С.
![]() .
Т.к. константу можно выносить за знак
предела.
.
Т.к. константу можно выносить за знак
предела.
![]() .
Трапеция вырождается в прямоугольник.
.
Трапеция вырождается в прямоугольник.
![]() f(x)dx.
Т.к. точки разбиения только поменяют
порядок.
f(x)dx.
Т.к. точки разбиения только поменяют
порядок.
Формула
Ньютона-Лейбница
![]() .
.
Методы нахождения определенного интеграла
Замена переменной в определенном интеграле и интегрирование по частям.
Теорема.
Если х=ф(t)
непрерывна на [
![]() ;
;
![]() ]
оси t
вместе со своей производной x’=ф’(t);
при изменении t
от
]
оси t
вместе со своей производной x’=ф’(t);
при изменении t
от
![]() до
до
![]() значение ф(t)
не выходит за пределы [a;b];
ф(
значение ф(t)
не выходит за пределы [a;b];
ф(![]() )=а
, ф(
)=а
, ф(![]() )
= b,
то для непрерывной на [a;b]
функции f(x)
справедливо равенство
)
= b,
то для непрерывной на [a;b]
функции f(x)
справедливо равенство
![]() f(x)dx=
f(x)dx=![]() f(ф(t))ф’(t)dt
(7.3)
f(ф(t))ф’(t)dt
(7.3)
называемое формулой замены переменной в определенном интеграле.
Док.
В самом деле
![]() f(t)dt=
F(b)-F(a)
, где F(x)
первообразная для f(x).
Т.к. при этом F(ф(t))
– есть первообразная для f(ф(t))ф’(t),
непрерывной на
f(t)dt=
F(b)-F(a)
, где F(x)
первообразная для f(x).
Т.к. при этом F(ф(t))
– есть первообразная для f(ф(t))ф’(t),
непрерывной на
[
![]() ;
;
![]() ],
то По Ньютону-Лейбницу имеем
],
то По Ньютону-Лейбницу имеем
![]() f(ф(t))ф’(t)dt
=F(ф(
f(ф(t))ф’(t)dt
=F(ф(![]() ))
- F(ф(
))
- F(ф(![]() ))=
F(b)-F(a)
=
))=
F(b)-F(a)
=![]() f(t)dt.
f(t)dt.
Комментарий. Имеются два подхода использования формулы замены. Один из них изложен выше. В другом (более употребимом) случае заменяют не переменную х, на некоторое выражение, а выражение, связывающее х заменяют одной переменной. А далее – как обычно. Не следует забывать также о смене пределов интегрирования в момент замены, чтобы не возвращаться к исходной переменной.
Интегрирование
по частям. Пусть u=ф(х)
и v=f(x)
непрерывны и дифференцируемы на [a;b].
Проинтегрируем равенство (uv)’=u’v+v’u
на этом отрезке и получим
![]() (uv)’dx=
(uv)’dx=![]() u’vdx
+
u’vdx
+![]() v’udx.
Но т.к. uv
есть первообразная для (uv)’,
то получаем
v’udx.
Но т.к. uv
есть первообразная для (uv)’,
то получаем
![]() v’udx
= uv
v’udx
= uv![]() -
-
![]() u’vdx
(7.3)
u’vdx
(7.3)
Формулу (7.3) называют формулой интегрирования по частям в ОИ
