u-lectures сопромат

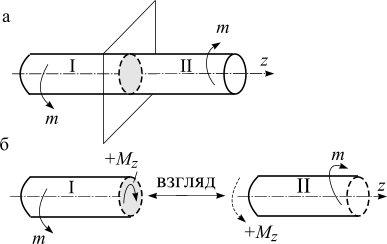
111

Если вал нагружен только двумя моментами, то из условия равновесия эти моменты всегда равны по величине и направлены в противоположные стороны (рис. 4.12, а). В других случаях крутящий момент определяют методом сечений. Вал рассекают плоскостью, мысленно отбрасывают одну часть, а ее действие на оставшуюся часть заменяют неизвестным крутящим моментом M к (рис. 4.12, б). Составляют уравнение равновесия для оставшейся левой

части:

∑mz = 0, ∑miz + M к = 0,

из которого и определяют значение момента:
M к = ∑miz .	(4.24)
отс.ч.

Крутящий момент, возникающий в произвольном сечении вала, численно равен алгебраической сумме внешних скручивающих моментов, приложенных к оставленной части.

Рис. 4.12

Правило знаков:

Условимся считать крутящий момент положительным, если внешний момент направлен против часовой стрелки при взгляде от сечения к любому концу

вала. Тогда положительный крутящий момент (Mz) изображается по часовой стрелке (рис. 4.12, б).

Например, для вала (рис. 4.12) крутящий момент в сечении I–I из равновесия:

–левой части M z1 = m1 − m2 ;

–правой части M z 2 = m4 − m3 .

Оба эти значения равны между собой, что видно из равенства (4.23).

112

Заметим, что принятое правило знаков не имеет физического смысла. Оно необходимо при построении эпюр. Положительные значения M z будем откла-

дывать вверх от базиса, отрицательные – вниз.

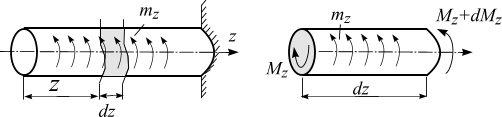
Иногда на вал действует распределенная моментная нагрузка интенсивности mz (рис. 4.13, а).

Вырежем малый элемент dz (рис. 4.13, б).

а

б

Рис. 4.13

Действие левой и правой отброшенной части вала заменим крутящим моментом, причем справа он имеет приращение dM z . Составим уравнение равнове-

сия:

∑mz = 0, M z − mz dz − (M z + dM z ) = 0 ,

Откуда
	dM z	= mz .	(4.25)
	dz

Производная крутящего момента по абсциссе сечения равна интенсивности распределенной моментной нагрузки.

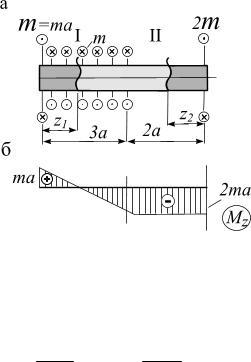
Пример. Построить эпюру крутящих моментов для вала (рис. 4.14, а). Скручивающие моменты изображены в виде двух кружочков: кружочек с точкой обозначает силу, направленную на наблюдателя, а кружочек с крестиком - силу от наблюдателя.

Решение: Разбиваем вал на два участка: I и II.

I участок, 0 ≤ z1 ≤ 3a;

лев.

M1 = ∑mi = m − mz1; (линейный закон)

z1 = 0, M1 = ma;

z1 = 3a, M1 = −2ma;

113

II участок 0 ≤ z2 ≤ 2a;

прав.

M 2 = ∑mi = −2ma, (const).

По полученным значениям строим эпюру M z (рис. 4.14, б).

Рис. 4.14

Для проверки используем зависимость (4.25). Вычислим первые производные на каждом участке:

dMdz1 = −m , dMdz2 = 0 .

Отсюда следует, что на I участке должна действовать распределенная моментная нагрузка m , а на II она отсутствует (рис. 4.14, а).

Напряжения при кручении круглого бруса

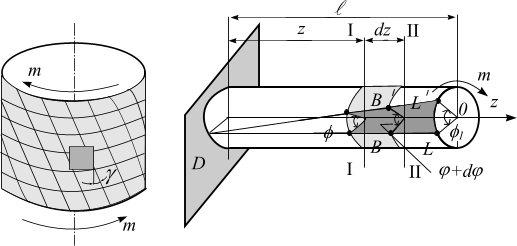
Представление о характере деформации кручения можно получить, подвергая скручиванию модель бруса с нанесенной на его поверхность сеткой продольных и поперечных линий.

После закручивания продольные линии превращаются в винтовые (рис. 4.15). Поперечные линии не искривляются, и расстояние между ними не меняется. Прямоугольники, образованные сеткой, перекашиваются за счет изменения первоначально прямого угла на малый угол γ.

Брус радиусом r (рис. 4.16) скручивается моментом m . Образующая DL после кручения перейдет в положение DL′. Сечение I–I повернется на угол ϕ, а сечение II–II на угол ϕ + dϕ. Следовательно, сечение II–II по отношению к I–I повернется на угол dϕ.

114

Рис. 4.15

Рис. 4.16

В результате наблюдений приходим к следующим гипотезам, на которых основана теория круглых валов:

1.Сечения, плоские до закручивания, остаются плоскими и после закручивания (гипотеза Бернулли);

2.Все радиусы данного сечения остаются прямыми и поворачиваются на один и тот же угол ϕ1 (рис. 4.16), т.е. каждое сечение поворачивается вокруг

оси z как жесткий тонкий диск;

3. Расстояния между сечениями не меняются, значит, продольные волокна не удлиняются и не укорачиваются, т.е. l = const .

На основании принятых гипотез кручение круглого бруса можно представить как результат сдвигов, вызванных взаимным поворотом сечений друг относительно друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения. Для их определения рассмотрим три стороны задачи. Статическая сторона задачи выражается интегральным уравнением равновесия:

M z = ∫τρdA,	(4.26)
A

т.е. крутящий момент M z представляет собой результирующий момент внут-

ренних касательных сил τ dA , действующих на бесконечно малых площадках сечения (рис. 4.17): ρ – плечо элементарной силы относительно продольной оси точки О.

115

Рис. 4.17

Рассмотрим геометрическую сторону задачи.

Выделим из бруса элемент dz (рис. 4.16) и рассмотрим картину деформирования, приняв левое сечение условно неподвижным (рис. 4.18).

Рис. 4.18

Радиус ОВ вместе с сечением поворачивается на угол dφ, а образующая CK произвольной точки K переходит в положение СК1, поворачиваясь на угол γ. Дуга KK1 = ρ dϕ, а из треугольника СКК1 отрезок KK1 = γ dz . Из равенства ρ dϕ = γ dz получим выражение угла сдвига на поверхности скручивания элемента, т.е. геометрическое уравнение,

γ = ρ	dϕ	.	(4.27)
	dz

Физическая сторона задачи определится законом Гука при сдвиге (4.5):

116

	γ =	τ	или τ = γ G .
		G

Проведем синтез трех сторон задачи. Формула (4.28) с учетом (4.27) принимает вид

τ = γ G = G ρ ddzϕ.

Подставляя (4.29) в (4.26), имеем:

	M z = ∫Gρ	dϕ	ρdA = G	dϕ	∫	2	dA ,
						ρ
		dz		dz
	A				A

где интеграл ∫ρ 2 dA = Jρ − полярный момент инерции сечения.

A

Из (4.30) следует:

dϕ = M z . dz GJρ

С учетом (4.31) формула (4.29) принимает окончательный вид

τ = M z ρ.

Jρ

(4.28)

(4.29)

(4.30)

(4.31)

(4.32)

По формуле (4.32) определяются касательные напряжения в любой точке поперечного сечения вала.

По закону парности такие же касательные напряжения возникают в продольных сечениях (рис. 4.19, а), и прямоугольный элемент испытывает состояние

чистого сдвига (рис. 4.19, б).

Анализ формулы (4.32) показывает:

1.Касательные напряжения τ распределены вдоль радиуса по линейному закону (рис. 4.19);

2.В каждой точке напряжения τ перпендикулярны текущему радиусу;

3.τ = 0 в центре круга ( ρ = 0);

4.Максимальные напряжения возникают в крайних точках сечения:

τmax =	M z	ρmax ,	(4.33)
	Jρ

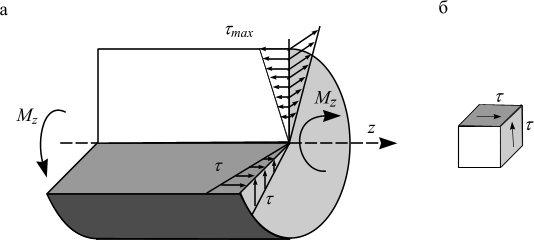
117

Рис. 4.19

				или	τmax	=	M z	,	(4.34)
							Wρ
	где W	=	Jρ	– геометрическая характеристика сечения, называемая поляр-
			ρ max
		ρ

ным моментом сопротивления, см3 или м3.

Общий вид эпюр крутящих моменты и углов закручивания вала

Скручивающая нагрузка в общем виде. Кручение бруса возникает от воз-

действия сосредоточенных и распределённых моментов относительно его оси. Для удобства расчёта введём понятие унифицированной схемы ступенчатого вала: пусть в начале каждого грузового участка приложен сосредоточенный момент Мi , и по всему участку действует распределённый момента интенсивности mi. Например, на рис. 4.20 приведена унифицированная схема ступенчатого вала с двумя участками. Для моментов используем известное правило знаков: при взгляде от заделки внешние положительные моменты направлены против хода часовой стрелки, такое направление показано на схеме вала. Чтобы упорядочить расчёт реального вала, внешние моменты нужно задавать числами со знаком, как это будет выполнено ниже.

Предлагаемая схема вала позволяет получить формулу для крутящих моментов и углов закручивания в общем виде, представить общий вид эпюр при кручении и хорошо демонстрирует их особенности.

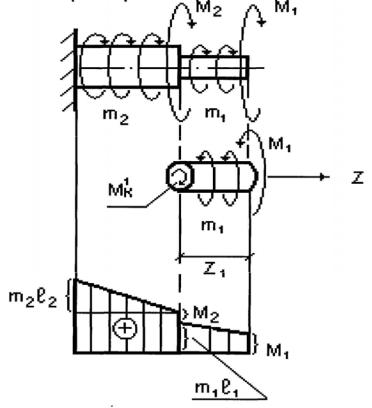
118

Рис.4.20 Унифицированная схема 2-х ступенчатого вала

Формула для вычисления крутящих моментов, общий вид их эпюр и за-

кономерности. Значения внутренних крутящих моментов Мк вычисляем методом сечений, выполняя последовательно правило РОЗУ (Разрезать, Отбросить, Заменить, Уравновесить). Рассмотрим вычисление крутящих моментов для двухступенчатого вала, представленного на рис. 4.20. В текущем сечении 1-го участка изобразим внутренний крутящий момент Мк, действующий по часовой стрелке (это общепринятое положительное направление). Запишем уравнение равновесия отсечённой части при кручении: сумма моментов относительно оси вала равна нулю, т. е.

∑ мом z= 0.

M1	−m z − M		1	= 0 , отсюда M1				= m z + M			1	.
кр	1	1					кр		1	1
Вычислим значения Mкр1		в начале участка (при z1=0) и в конце участка (при
z1=l1). Получим	M1	(0) = M				и M1	(l ) = M		+m l .
					1			1
	кр					кр	1			1 1

Рассуждая аналогично для 2-го участка, получим в текущем сечении, удалённом от его начала на расстоянии z2,

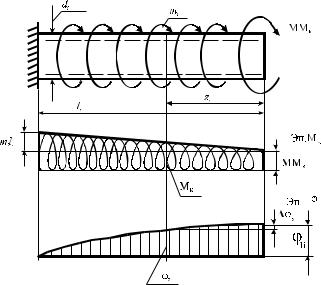
119

Mкр2 = Mкр1 (l1 ) + M2 +m2 z2 .

В начале участка (при z2 = 0) и в конце (при z2 = l2) имеем

Mкр2 (0) = M1(l1 ) + M2 и Mкр2 (l2 ) = M1(l1 ) + M2 +m2l2 .

По этим значения построим эпюру Мк в общем виде (см. рис. 4.20). Она будет нарастающей от свободного края по линейному закону. По ней хорошо прослеживаются особенности эпюры крутящих моментов. Подставляя цифровые значения моментов реального вала, можно получить для него эпюру Мк.

Для компактного представления изложенной методики вычисления крутящих моментов можно изобразить только один грузовой участок вала (рис. 4.21), это любой участок вала, который представляем по унифицированной схеме. Тогда запишем для крутящего момента общую формулу

M i	= MM i +m z	i	(4.35)
кр	i

где MM i − значение крутящего момента в начале i-го участка.

Можно сказать, что любой участок вала или одноступенчатый вал можно представить такой унифицированной схемой, как показано на рис. 4.21, и использовать одну и ту же формулу для крутящего момента (4.35).

Рассмотрим пример вычисления крутящего момента (рис. 4.22). Здесь для левого вала M=1,2 кН·м, m= -8 кН·м /м

Запишем крутящий момент по (4.35).

Рис. 4.21 Унифицированная схема грузового участка ступенчатого вала

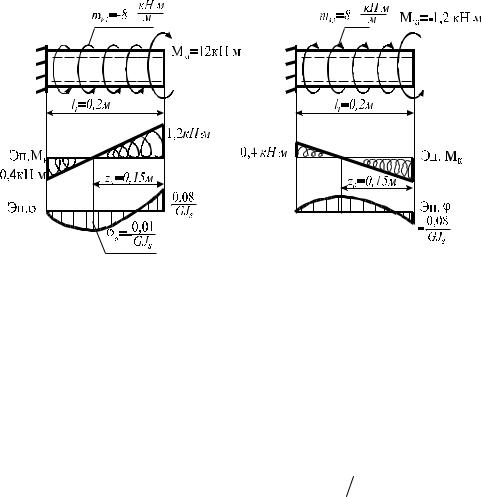
120

Получим Mкр =1,2 +(−8) z . Вычислим значения момента в начале и в конце

вала: при z = 0 Mкр =1,2 кН·м, при z = 0,2м Mкр = −0,4 кН·м.

Рис. 4.22 Эпюры крутящих моментов и углов закручивания

Отложив полученные значения от базисной линии, проведём согласно с линейной функцией (4.35) прямую линию эпюры крутящих моментов.

Формула для вычисления углов закручивания вала, общий вид их эпюр и закономерности. Для нахождения углов закручивания сечений нужен угол закручивания i-го участка Δϕi , который с учётом (4.35) принимает выражение

li	Mкрi		(MMi li +mi li2 2)
Δϕi = ∫		dz =	G JR	.	(4.36)
	G JR
0	i		i

Реальный угол закручивания свободного края φ11 (это первое сечение на 1-м участке) является суммой угловых деформаций всех участков (рис. 4.25):

i=n

φ11= ∑ φi. i=1

Записанные формулы позволяют вычислить углы закручивания любого сечения унифицированного вала (рис. 4.21) и построить эпюру углов закручивания ϕ, она будет нарастающей от заделки по кривой 2-го порядка. Подставляя цифровые значения моментов и размеры реального вала, можно получить углы закручивания и эпюры для реального вала.