u-lectures сопромат

21

σz

Рис. 1.13

Нормальные и касательные напряжения, если будет одновременно иметь место сдвиг и отрыв (в этом случае появится полное напряжение P ).

Выделим в окрестности рассматриваемой точки A элементарный объем материала в виде бесконечно малого элемента (БМЭ) – параллелепипеда. На его гранях действуют касательные и нормальные напряжения (рис. 1.13, б).

Совокупность этих напряжений носит название тензора напряжений:

Tн =	σx	τyx	τzx
	τxy	σy	τzy
	τxz	τyz	σz

Если поворачивать параллелепипед, то напряжения на его гранях будут изменяться. И в некотором положении касательные напряжения будут равны нулю:

τyx = τxy = τxz = τzx = τyz = τzy = 0 .

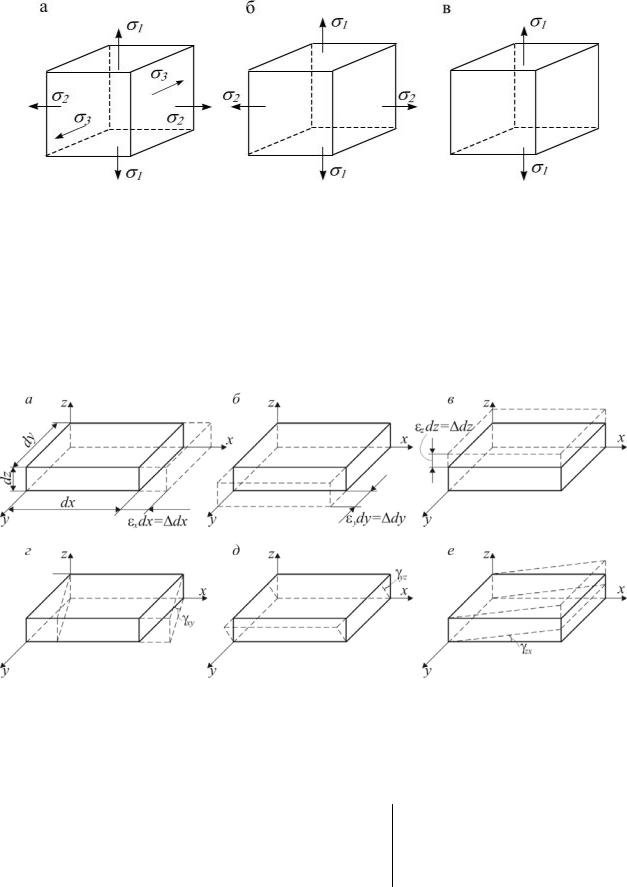
Площадки, на которых τ = 0, называются главными, а нормальные напряжения на этих площадках – главными напряжениями σ1 , σ2 , σ3 , при этом при-

нимают σ1 ≥ σ2 ≥ σ3 . В этом случае возникает объемное (трехосное) напря-

женное состояние (рис. 1.14, а).

Если одно из главных напряжений равно нулю, то напряженное состояние (н.с.) называется плоским (двухосным) (рис. 1.14, б). Если равны нулю два главных напряжения, то напряженное состояние называется линейным (одно-

осным) (рис. 1.14, в).

Линейное н.с. имеет место в стержнях, работающих на растяжение или сжатие, в некоторых точках стержня, работающего на изгиб или сложное сопро-

22

тивление.

Рис. 1.14

Плоское н.с. имеет место при кручении, сдвиге, изгибе и сложном сопротивлении бруса. В условиях плоского н.с. работают элементы в виде пластин и оболочек (панели, перегородки, стенки и днища резервуаров, листовые конструкции).

Объемное н.с. возникает в материале дорожного покрытия в месте давления колеса на плиту покрытия, в месте контакта колеса с поверхностью рельса, аналогично в грунтовом массиве.

Рис. 1.15

Аналогично понятию тензора напряжений введем понятие тензора деформаций (рис. 1.15), который полностью определяет деформированное состояние в точке тела:

TД =	εx	εyx	εzx
	εxy	εy	εzy
	εxz	εyz	εz

23

	εxy =	1	γxy ,	εxz =	1	γxz , …
		2			2

Сдвиговые деформации:

γ yx = γxy ; γzy = γ yz ; γxz = γzx .

Тема 1.4 Модель прочностной надежности

Всё большее значение для современных конструкций приобретает на столько прочность, сколько надежность, т. е. способность конструкций сохранять свои показатели в течение требуемого периода времени.

Допустимый срок службы конструкции, называемый ресурсом, указывается либо временем работы, либо числом циклов нагружений.

Свойство конструкции сохранять свои качества в течение требуемого периода времени называют надежностью. Совместить понятия прочность и надежность конструкции можно с помощью прочностной надежности, под которой понимается отсутствие отказов, т. е. нарушений в работе конструкции в течение требуемого ресурса. Количественной характеристикой прочностной надежности используют вероятность A события и вероятность B разрушения:

A = m , B =1− A.	(1.6)
n
где m – число испытаний, при которых событие наблюдалось,
n – общее число испытаний, например,	A = 0,95 означает, что в течение ре-

сурса из ста конструкций может отказать пять.

Нахождение вероятности разрушения на стадии проектирования в настоящее время еще сложная задача. Качество конструкции сейчас оценивают запасом прочности, под которым понимается

n =	σкр	≥ [n],	(1.7)
	σmax

здесь σкр – критическое значение параметра, нарушающее работоспособ-

ность (например, параметры коррозии, старения и др.),

σmax – наибольшее значение этого параметра при работе конструкции, [n] – допустимое значение запаса, которое назначается, исходя из опыта

эксплуатации, например, при случайных нагрузках [n]= 3 −5.

Модель прочностной надежности можно построить, если смоделировать (или схематизировать) свойства материала и формы конструкции, создать модель

24

(или схему) нагружения и разрушения. В итоге этих рассмотрений получают запас прочности (1.7) и вероятность разрушения (1.6).

Реальное строение и три модели строения материалов

В качестве конструкционных материалов в машиностроении используют металлы и сплавы, которые имеют кристаллические строения. К настоящему времени появление деформаций и разрушения металлов и сплавов хорошо объясняется с помощью дислокационной теории строения реального материала, но нужно отметить, что схематизация (или модель) реального материала должна отвечать задачам определенной отрасли науки, например, металловедение и детали машин имеют разные цели и методы исследования. В виду этого сформированы три вида моделей материала.

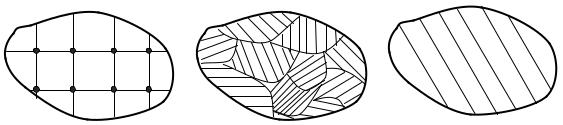
Физической называют модель, когда схематизируется кристаллическое строение (рис. 1.16, а). Оно изображается в виде кристаллической решетки атомов. Такая схема нужна в физике твердого тела.

а)	б)	в)
	Рис. 1.16 Модели строения материалов

Инженерно-физическая модель (рис. 1.16, б) рассматривает сплавы металлов как совокупность зерен с различной ориентацией кристаллической решетки, которые образуются в процессе охлаждения и кристаллизации. Эта модель позволяет объяснить особенности материала и служить основой для изучения металлов и сплавов.

Инженерная модель (рис. 1.16, в) это модель сплошной среды, при которой материал заполняет весь объем сплошным образом, без пустот и раковин. Она определяет свойства и служит для оценки прочности и жесткости конструкции в целом. Инженерная модель сплошной среды позволяет рассматривать тело как непрерывную среду и применять методы математического анализа, характеризовать упругость, пластичность и ползучесть материала.

Контрольные вопросы к разделу 1.

1.Перечислите основные задачи предмета сопротивление материалов.

2.Что такое расчетная схема объекта?

25

3.Укажите геометрические признаки стержня, оболочки и массивного тела.

4.Что такое сосредоточенная сила, распределенная нагрузка и момент?

5.Какие типы опор вам известны? Какие перемещения они ограничивают?

6.Какие силы можно считать распределёнными по линии, сосредоточенными в точке? Приведите примеры.

7.Поясните суть метода сечений.

8.Дайте определение каждого из шести внутренних силовых факторов

9.Перечислите виды простого и сложного сопротивления стержня.

10.Дайте определение понятия «напряжения». Какие виды напряжения Вы знаете?

11.Поясните, что такое тензор напряжений, линейное, плоское и объемное напряженное состояния.

12.Что такое линейная и угловая деформация, тензор деформации?

13.Сформулируйте принцип независимости действия внешних сил.

14.Что такое упругое тело?

15.Назовите основные допущения и гипотезы СМ.

16.В чем состоит модель прочностной надежности?

17.Перечислите известные вам предельные состояния конструкций и приведите примеры

26

Раздел 2 Центральное растяжение (сжатие) прямого стержня

Тема 2.1 Расчёты центрально растянутого (сжатого) прямого стержня

Осевым (центральным) растяжением или сжатием называют такой вид де-

формации, при котором в поперечном сечении бруса возникают только продольная сила N.

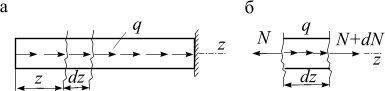
Дифференциальная зависимость между q и N Построение эпюры продольных сил

Рассмотрим стержень, нагруженный продольной распределенной нагрузкой, интенсивностью q (рис. 2.1, а). Выделим из стержня элемент длиной dz (рис. 2.1, б). На него будут действовать нагрузка q и продольные силы: в левом сечении – N, в правом – (N+dN), заменяющие действие отброшенных частей бруса, где dN – приращение продольной силы на участке dz.

Рис. 2.1

Составим уравнение равновесия для выделенного элемента:

∑Z = 0, − N + qdz + N + dN = 0,
откуда
	dN	= −q.	(2.1)
	dz

Производная от продольной силы по длине бруса равна интенсивности рас-

пределенной нагрузки q. По знаку производной можно судить о росте или убывании функции. Если q >0, то продольная сила убывает. Зависимость

(2.1) используется при проверке правильности построения эпюры N . Продольная сила N в сечении численно равна алгебраической сумме проекций на ось Z всех внешних сил, включая и опорные реакции, действующие на отсеченную часть бруса, взятых со знаком плюс, если они направлены от сечения (растяжение), и минус – если к сечению (сжатие):

N = ∑Z(Fi )отс.ч.

(2.2)

27

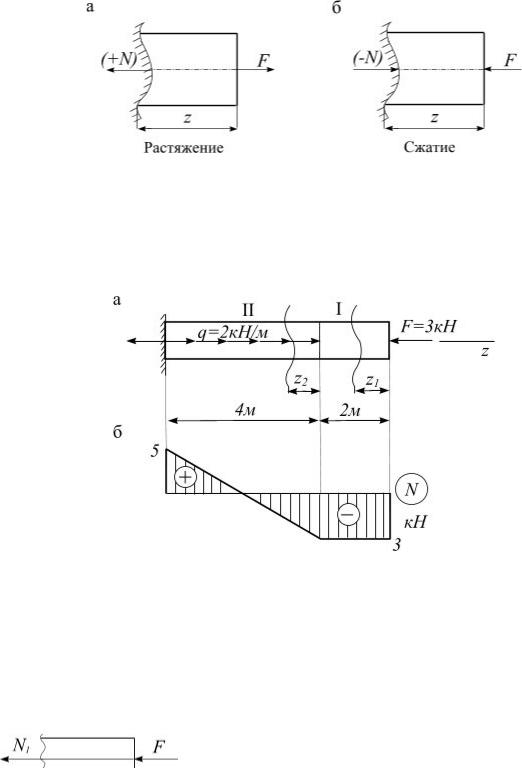
Знак продольной силы N определяется по схеме: растяжение – со знаком

«+» (рис. 2.2, а), сжатие – со знаком «–» (рис. 2.2, б).

Рис. 2.2

Пример 2.1. Для бруса (рис. 2.3, а) построить эпюру продольных сил N. Определим реакцию заделки.

∑Z = 0, − H + q 4 − F = 0, H = q 4 − F = 2 4 − 3 = 5кH.

Рис. 2.3

Разобьем брус на два участка, и, применив метод сечений, найдем продольные силы на каждом из них, рассматривая равновесие отсеченной части. Во избежание ошибки следует внутреннее усилие принимать всегда положительным (направлять от сечения).

Участок I 0 ≤ z1 ≤ 2 м

∑Z = 0, − N1 + F = 0,

N1 = −F = −3 кН(const).

На первом участке продольная сила постоянна и отрицательна.

28

Участок II

0 ≤ z2 ≤ 4м

q= 0, − N2 + qz2 − F = 0,

+qz2 − F.

На этом участке продольная сила изменяется по линейному закону.

при z2 = 0,	N2 = −F = −3кН,
при z2 = 4 м,	N2 = −F + q 4 = 5кН.

По найденным значениям продольных сил на отдельных участках строим эпюру N (рис. 2.3, б).

Примечание

Для бруса, закрепленного с помощью заделки, для построения эпюры, не обязательно определение опорных реакций, если оставлять часть бруса, которая не закреплена.

Знак усилия N , получаемый из решения, позволяет установить вид деформации – растяжение или сжатие.

На участке I, где q = 0 , эпюра N – прямая, параллельная оси ( N = const ).

На участке II, где q ≠ 0 , эпюра N – наклонная прямая (N изменяется по линейному закону).

В сечениях, где приложены внешние силы, внутренняя сила меняется скачкообразно, причем размер скачка равен соответствующей внешней силе. Так, скачок на уровне заделки характеризует значение реакции (Н=5 кН), скачок на свободном конце – значение внешней силы (F=3 кН).

Напряжения в поперечных сечениях стержня

Вывод формул для напряжений в стержнях будем всегда проводить по приведенной ниже схеме:

Статическая сторона задачи – запись интегральных уравнений равновесия;

Геометрическая сторона задачи – изучение деформаций на основе опыта и гипотез;

Физическая сторона задачи определяется законом Гука; Синтез – совместное решение полученных уравнений.

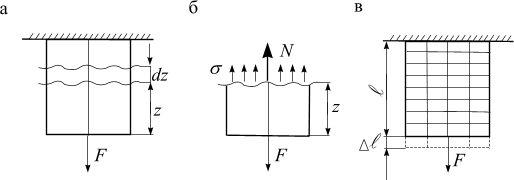
Рассмотрим стержень, нагруженный силой F (рис. 2.4 а). Для произвольного сечения z (рис. 2.4, б) статическая сторона задачи выражается уравнением

29

N = ∫σ dA,	(2.3)
A

где А – площадь поперечного сечения бруса.

Рассмотрим модель стержня (рис. 2.4, в), на боковой поверхности которого нанесена ортогональная сетка из продольных и поперечных линий.

Рис. 2.4

После нагружения можно заметить, что поперечные линии смещаются вдоль продольной оси, оставаясь прямолинейными и перпендикулярными ей. Это подтверждает гипотезу плоских сечений Я. Бернулли:

Сечения бруса, плоские и перпендикулярные его продольной оси до деформации, остаются плоскими и перпендикулярными оси в процессе деформации.

Продольные линии (волокна) удлиняются на одну и ту же величину		l (рис.
2.4, в), и их относительное удлинение одинаково.
Геометрическая сторона задачи выражается уравнением
ε =	l = const .	(2.4)
	l

Физическая сторона задачи заключается в установлении зависимости деформаций от напряжений. При упругих деформациях эта зависимость линейна, и, как известно, называется законом Гука:

ε = σ	или σ = ε E ,	(2.5)
E
где E = const для однородных	и изотропных материалов,	следовательно,
σ = const .
Из уравнений (2.3-2.5) получаем
N = ∫σ dA = ∫εE dA = εE∫dA = εEA = σ A.		(2.6)

A A

30

Окончательно

σ =	N	.	(2.7)
	A

В поперечном сечении бруса при растяжении (сжатии) возникают равномерно распределенные нормальные напряжения, равные отношению продольной силы к площади сечения (рис. 2.4, б).

Формула (2.7) справедлива лишь для сечений, достаточно удаленных от мест приложения нагрузки. При расчетах руководствуются принципом Сен-Венана,

который можно изложить так: способ приложения внешних сил влияет на распределение напряжений только в области их приложения.

Поэтому, нарушение равномерности распределения напряжений вблизи мест приложения нагрузки, носит местный характер. При расчетах эта часть стержня исключается из рассмотрения, что позволяет пользоваться формулой

(2.7).

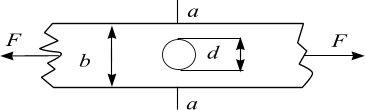
Исследования показали, что равномерное распределение напряжений по площади сечения на основании (2.7), будет только в тех случаях, когда по длине стержня поперечные сечения постоянны. Резкие изменения поперечного сечения (отверстия, канавки) приводят к неравномерному распределению напряжений, вызывают концентрацию напряжений. При наличии ослабления в пластине (например, заклепочными отверстиями, рис. 3.6) следует вводить площадь нетто Anet = A − Aослаблен..

Рис. 2.5

На основе предположения об отсутствии концентрации напряжений по формуле (2.7) вычисляется среднее напряжение в ослабленном сечении пластины:

σ =	N	.	(2.8)
	A
	net
Например, для сечения а–а, пластины (рис. 2.5) Anet = (b − d )×δ , где δ			–

размер пластины в направлении, перпендикулярном плоскости чертежа.

Напряжения в наклонных сечениях