u-lectures сопромат

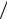
	201
ε		= σ1 .
11		E
Коэффициент Пуассона:
ν =		εпоп.		.
		εпрод.
Деформация ε 22= σ2 E – продольная деформация в направлении σ2 , тогда

деформация ε 12 , т. е. по направлению σ1 от действия σ2 , будет поперечной по отношению к направлению σ2 , и из уравнения Пуассона получим:

−	ε12	=ν,	отсюда ε12	= −	σ2	ν.
Аналогично	ε22				E
			= − σ3 ν.
		ε
	13		E

Полная относительная деформация ε1 в направлении σ1 получается в резуль-

	тате суммирования ε11, ε12 ,		ε13.
	ε =			1				[σ − ν(σ			2	+ σ	3	)]
	1				E			1
	ε2		=			1		[σ2 − ν(σ1				+ σ3 )]			(6.13)
						E
	ε	3	=		1			[σ	3	− ν(σ + σ			2	)]
						E					1

Формулы (6.13) – выражают обобщенный закон Гука, где ε 1 , ε 2 , ε 3 - глав-

ные деформации.

σ3 = 0 , тогда

При плоском напряженном состоянии

ε =

1

(σ −ν σ

2

); ε

2

=

1

(σ

2

− ν σ );

ε

3

= −

ν

(σ + σ

2

).

(6.14)

1

E

1

E

1

E

1

При линейном напряженном состоянии σ2 = σ3 = 0; σ1 = σ:

ε1

=

σ

,

ε2 = −

νσ

, ε3

= −νσ .

(6.15)

E

E

E

202

Обратная форма закона Гука

Плоское напряженное состояние (н. с.)

Перепишем уравнения (6.14) для ε1 и ε2 и сложим левые и правые части:

ε = σ1

−ν σ2 ; νε

2

= ν σ2

− ν νσ1

1

E

E

E

E

ε + νε

2

= σ1

− ν2 σ1 ;

1

E

E

отсюда обратная форма закона Гука

σ =

E

(ε

+ νε

)

1−ν2

1

1

2

(6.16)

E

.

σ

=

(ε

+ νε )

2

2

2

1−ν

1

Линейное напряженное состояние (н.с.)

σ1 = ε1E.

(6.17)

По формулам (6.16) и (6.17) можно найти главные напряжения через главные деформации.

Тензор напряжений. Напряжения на произвольной площадке. Обобщенный закон Гука для произвольной площадки

Рассмотрим элемент dxdydz (рис. 6.4). Полные напряжения на гранях пред-

ставляют нормальными и касательными составляющими. Совокупность этих напряжений носит название тензора напряжений:

Tн =	σ x	τ yx	τzx	.
	τxy	σ y	τzy
	τxz	τ yz	σ z

203

Рис. 6.4

Считаем, что нормальные напряжения вызывают линейные деформации ребер dx, dy, dz по направлениям x, y, z - εx , εy , εz .

Касательные напряжения вызывают изменения прямых углов, т.е. сдвиговые деформации:

γyx = γxy ;γzy = γyz ;γxz = γzx .

Тогда обобщенный закон Гука примет вид

εx = E1 σx − ν(σy + σz ) ;

εy = E1 σy − ν(σx + σz ) ;

εz = E1 σz − ν(σx + σy ) ;

γyx	= γxy	=		τxy			;
				G
γzy	= γyz	=		τyz		;		(6.18)
				G
γxz	= γzx	=	τzx		.
				G

Формулы (6.18) – обобщенный закон Гука для произвольной площадки. При плоском напряженном состоянии σ z = 0 (рис. 6.5).

εx	=	1			(σx − νσy )
		E
		1
εy	=				(		σy − νσx )
		E
											(6.19)
					ν
εz	= −							(σx + σy )
				E
									τxy
γyx = γxy							=
									G

Рис. 6.5

204

Изменение объема. Удельная потенциальная энергия упругой деформации

Относительное изменение объема при объемном напряженном состоянии:

θ = V −V0 ,

V0

где V0 = abc – объем до деформации; V – объем после деформации.

Под действием σ1 , σ2 , σ3 стороны параллелепипеда получают удлинение

a , b ,	c . Тогда
V = (a +	a)(b + b)(c + c) = a b c (1+	a)(1+	b)(1+			c) =
=V0 (1+ ε1)(1+ ε2 )(1+ ε3 );		a	b			c
	θ = V0 (1+ε1)(1+ ε2 )(1+ ε3 ) −V0	= (1+ ε )(1		+ ε	2	)(1	+ ε	) −1 =
	V0		1				3

=1+ ε1 + ε2 + ε3 + ε1ε2 + ε2ε3 + ε1ε3 + ε1ε2ε3 −1.

Так как ε1 , ε2 , ε3 малы, то их произведениями пренебрегаем. Тогда объемная деформация будет равна сумме главных деформаций:

θ ≈ ε1 + ε2 + ε3 .

(6.20)

Если рассматривать средние значения деформаций и напряжений в виде

εср =	ε1 + ε2 + ε3	;σср =	σ1 + σ2 + σ3	,	(6.21)
	3		3

действующих согласно (6.11) на октаэдрических площадках, получим:

θ = 3εср .

(6.22)

Если в (6.20) и (6.21) подставить закон Гука (6.13), то можно объемную деформацию выразить через напряжения:

205

θ= 3ε

ср

=

1− 2ν3σ

ср

=

1− 2ν (σ + σ

2

+ σ

) .

E

E

1

3

Тогда:

θ

1− 2ν

1− 2ν

εср =

=

3σср

=

σcp .

(6.23)

3

E3

E

По выражению (6.23) можно оценить предельное значение коэффициента Пуассона – коэффициента поперечной деформации. При положительных σср ве-

личина θ должна быть положительна, при отрицательных σср отрицательной должна быть и величина θ. Это возможно, когда:

1−E2ν ≥ 0 → ν < 12 .

Потенциальная энергия деформации при простом растяжении:

U= 1 σε = σ2 . 2 2E

При объемном напряженном состоянии:

			U = 1		σ ε +		1	σ	ε		+	1	σ	ε	.
			2		1	1	2	2		2		2	3	3
Подставим значения ε1 , ε2 , ε3				по закону Гука (6.13):
	1	2	2			2
U =			+ σ2	+ σ3 − 2ν(σ1σ2												(6.24)
	2E σ1											+ σ2σ3 + σ1σ3 ) .

Уравнение (9.24) определяет полную потенциальную энергию, которая включает в себя энергии изменения объема U0 и формы Uφ тела:

U =U0 +Uφ .

Объемная деформация θ определяет только энергию изменения объема. Так как величина θ связана с εср и σср , то энергия изменения объема будет:

206

U

0

=

1

σ

cp

ε

cp

+

1

σ

cp

ε

cp

+ 1 σ

cp

ε

cp

= 3 σ

cp

ε

cp

=

2

2

2

2

(6.25)

=

3 (σ1 + σ2 + σ3 ) 1− 2ν (σ1 + σ2 + σ3 )

= 1− 2ν

(σ + σ

+ σ

)2 ,

2

3

E

3

6E

1

2

3

144424443

εcp

Если из общей энергии U вычесть энергию изменения объема U0 , то полу-

чим энергию формоизменения:

Uφ =U −U0 = 13−Eν (σ12 + σ22 + σ32 −σ1σ2 − σ2σ3 −σ1σ3 ) =

(6.26)

= 16+Eν (σ1 −σ2 )2 +(σ2 −σ3 )2 +(σ1 −σ3 )2 .

При простом растяжении σ2 = σ3 = 0,

U	0	=	1− 2ν σ2		; U	φ	=	1+ ν σ2.		(6.27)
			6E	1				6E	1

Чистый сдвиг: σ1 = τ, σ3 = −τ, σ2 = 0 . По (6.23) и 6.25) имеем:

θ = 1−E2ν(τ −τ +0), U0 = 1−6E2ν(τ −τ +0)2 = 0 ,

т. е. при чистом сдвиге объем не меняется, и энергия изменения объема равна нулю. Следовательно, потенциальная энергия накапливается только за счет изменения формы (6.26):

	U =Uф =	1+ν 6τ2		=	τ2	,
					2G
			6E
	где		E
	G =			.
			2(1+ν)

Анизотропия

207

В общем случае анизотропного линейно-упругого тела закон Гука можно представить в виде

σij = Сijkl εij

(6.28)

где σij - тензор напряжений, εij - тензор деформаций, тензор четвертого ранга

Сijkl - тензор упругих постоянных. Подробно данный вопрос рассматривается

вкурсе «Теория упругости».

Прямая задача при плоском напряженном состоянии. Круг Мора

Аналитическое решение прямой задачи дается формулами (6.5). Графически σα , τα , σβ , τβ по известным σ1 , σ2 (рис. 6.6, а) определяются с помощью

круга Мора (рис. 6.6, б).

Круг Мора (круг напряжений) – геометрическое место точек, абсциссы и ординаты которых равны соответственно нормальным и касательным напряжениям, возникающим на площадках данной серии.

τα

Рис. 6.6

Серией площадок называют совокупность бесчисленного множества площадок, перпендикулярных одной и той же грани элементарного параллелепипеда.

Порядок построения

1.На плоскости выбирается ось σ (ось абсцисс) параллельно 1–му главному напряжению.

2. Выбирается ось ординат – ось касательных напряжений τ.

3.На оси абсцисс откладываются главные напряжения σ1 , σ2 (с учетом их

208

знаков), и на разности этих напряжений, как на диаметре, строится круг напряжений (круг Мора). Точка В характеризует напряжения по вертикальным боковым граням параллелепипеда, изображенного на рис. 6.6, а, а точка А – по его горизонтальным граням.

4.Из точек В и А проводятся лучи параллельные нормалям к соответствующим граням, до пересечения с окружностью в точке К, называемой полюсом. Затем из точки К проводится луч, параллельный нормали nα ; точка пересече-

ния луча с кругом Mα определяет напряжения σα, τα на площадке α .

5. Из этой же точки проводится луч, параллельный нормали nβ, пересечение которого с кругом Мβ дает σβ и τβ (рис. 6.6, б). Из построений можно получить формулы 6.5:

σα = ONα = OB − BNα = OB − MαB sin α =

=OB −(AB sin α) sinα = σ1 − (σ1 −σ2 ) sin α sin α =

=σ1 −σ1 sin2 α + σ2 sin2 α = σ1 (1−sin2 α) + σ2 sin2 α;

σα = σ1 cos2 α + α2 sin2 α.

Аналогично для σ	:	σ	β	= σ sin2	α +σ	2	cos2	α.
β				1

τα = NαMα = MαB cosα = (AB sin α) cos = σ1 −2 σ2 sin 2α.

Обратная задача. Определение главных напряжений с помощью круга Мора

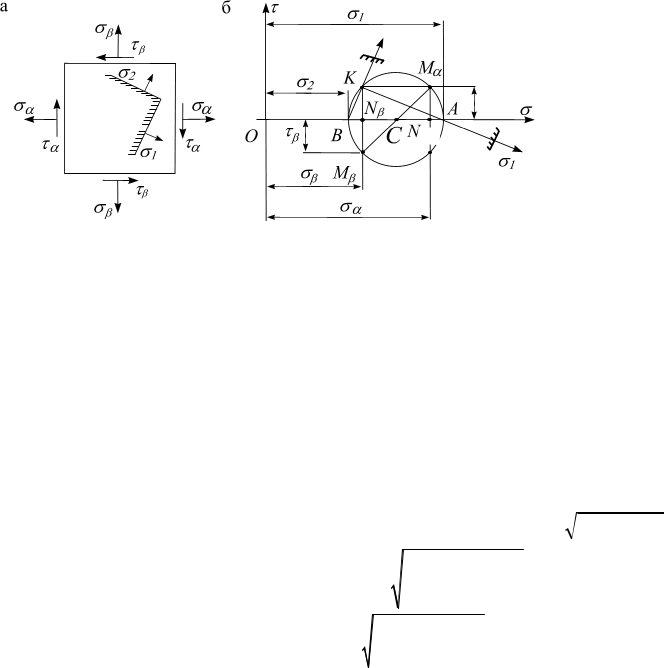
Известно σα , τα , σβ , τβ (рис. 6.7, а). Пусть σα > σβ; τα > 0, τβ < 0 . Определить

σ1 , σ2 .

1.Ось абсцисс параллельна большему из напряжений σα (рис. 6.7, б).

2.Ось касательных напряжений перпендикулярна оси нормальных напряжений.

3.На оси абсцисс откладываются σα , σβ (точки Nα и Nβ ).

4.Из концов σα и σβ откладываются отрезки τα и τβ (точки Mα и Mβ ), концы τα и τβ соединяются.

209

τα

С

Рис. 6.7

5.На линии, соединяющей концы τα и τβ , как на диаметре, строится

круг Мора, который отсекает на оси абсцисс отрезки ОА и ОВ, равные σ1 и

σ2 .

6. Из точек Mα и M β проводят лучи параллельные нормалям к вертикальной

и горизонтальной граням параллелепипеда до пересечения с окружностью в точке К (полюс круга). Направления σ1 и σ2 получатся, если точки А и В со-

единить с полюсом К круга Мора, имеющего координаты (σβ и τα ). Из построений можно получить выражения для главных напряжений:

σ1 = OC + CB = OC + CMα = OC + 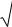CNα2 + NαM

σ

α

+σ

β

σ

α

−σ

β

2

=

+

+τα2 ;

2

2

σ

α

+ σ

β

σ

α

−σ

β

2

σ2 = OA = OC − AC = OC −CMα =

−

+ τα2 ;

2

2

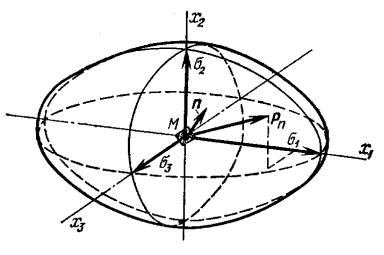
Эллипсоид напряжений

Интерпретация поверхности напряжений в виде эллипсоида была предложена Ламе (1795-1870). Координатные оси совместим с главными осями тензора напряжений для некоторой точки М. При таком положении касательные напряжения будут равны нулю, а нормальные равны главным σ1 , σ2 , σ3 .

Уравнение эллипсоида напряжений (или эллипсоида Ламе) с полуосями, равными главным напряжениям σ1, σ2, σ3 имеет вид:

210

		x2	+		x2	+		x2	=1	(6.29)
		1			2			3
	σ 2			σ 2			σ 2
	1			2			3

Рис. 6.8

Поверхность эллипсоида представляет собой геометрическое место концов векторов напряжений pn на всем множестве площадок, проходящих через данную точку М.

Выводы о напряженном состоянии:

1.Наибольшее напряжение в рассмотренной точке тела равно максимальному из трех главных напряжений в этой точке.

2.Если ни одно из трех главных напряжений не равно нулю, то векторы полных напряжений на всем множестве площадок, проходящих через данную точку тела, располагаются в объеме эллипсоида Ламе. Такое напряженное состояние в точке тела называется объемным или трехосным. В зависимости от знаков главных напряжений это есть растяжение или сжатие в направлении трех главных осей тензора.

3.Если одно из главных напряжений равно нулю, то эллипсоид превращает-

ся в эллипс, что соответствует плоскому или двухосному напряженному состоянию.

4.Если два главных напряжения равны нулю, то элемент превращается в отрезок прямой линии, расположенной на одной из главных осей тензора на-

пряжений, что соответствует линейному или одноосному напряженному состоянию.

Тема 6.2 Экспериментальное определение напряжений и деформаций

Классификация экспериментальных методов