u-lectures сопромат

221

Если выполняется условие
F (σ1,σ2 ,σ3 ) < C ,	(6.31)

то материал, согласно критерию пластичности, не переходит в пластическое состояние, сохраняя упругие свойства, а, согласно критерию разрушения, в материале не образуется трещин, приводящих к разрушению.

Условие (6.30) геометрически интерпретируется в трехмерном пространстве σ1 − σ2 − σ3 поверхностью, ограничивающей область безопасных напряжен-

ных состояний с точки зрения наступления текучести или разрушения.

Основные теории прочности

Критерии пластичности. Критерий наибольших касательных напряжений. III теория прочности

Пластическая деформация обусловлена сдвигами кристаллической решетки металла, приводящими к возникновению плоскостей скольжения – линии Людерса – Чернова.

Предполагается, что критерий наступления пластического состояния связан с достижением некоторой функцией F (σ1,σ2 ,σ3 ) величины наибольшего каса-

тельного напряжения τmax , т.е.

F(σ1, σ2 , σ3 ) = C = τmax .

(6.32)

При объемном напряженном состоянии:

	τmax =	σ1 − σ3	= C .	(6.33)
		2

С другой стороны, в условиях одноосного растяжения, при которых проводятся испытания по определению механических свойств материалов, предельное состояние наступления пластических деформаций опишется соотношением:

σ 2= σ 3= 0 ; σ 1 = σт ; тогда τmax = σт 2 = C ,	(6.34)
где σт – предел текучести при одноосном растяжении.
Сопоставляя (6.33) и (6.34), получим условие пластичности в виде
F(σ 1,σ 2,σ 3 )= σ 1 −σ 3 = σт .	(6.35)

222

Критерий наибольших касательных напряжений был предложен Ш. Кулоном (1773 г.), а в качестве условия пластичности Г. Треска (1868 г.) и впоследствии математически обоснован Сен-Венаном.

Условие (6.35) не учитывает влияние среднего напряжения σ 2 на наступле-

ние пластического состояния, однако эксперименты Лоде (1926 г.) показали, что это влияние необходимо учитывать.

Энергетический критерий.

Критерий наибольших октаэдрических касательных напряжений. IV теория прочности

Губер (1904 г.) и Генки (1924 г.) предположили, что критерий достижения пластического состояния должен быть связан с накопленной в единице объема удельной потенциальной энергией деформации, а именно с той ее частью, которая связана с энергией формоизменения Uф. Была исключена из рас-

смотрения энергия изменения объема Uоб, т.к. при всестороннем сжатии (σ1= σ 2= σ 3= −σ) пластические деформации не возникают, а потенциальная энергия деформации возрастает. Итак, когда энергия формоизменения Uф, соответствующая некоторой функции F (σ1,σ2 ,σ3 ), достигнет предельного значения, наступает состояние текучести, т. е.

F(σ1,σ2 ,σ3 ) = C =Uф.

(6.36)

При объёмном напряженном состоянии:

Uф = 16+Eν [(σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ1 − σ3 )2 ]= C . (6.37)

При чистом сдвиге U0 = 0 , и изменение потенциальной энергии деформации происходит только за счет энергии формоизменения Uф.

При одноосном растяжении предельное состояние описывается соотношениями:

σ = σ

;

σ

2

= σ

3

= 0;

U

ф

= 2

1+μ

σ2

= C .

(6.38)

1

Т

6E

Т

Тогда условие пластичности будет в виде

223

F(σ , σ	2	, σ	3	) =	1	(σ − σ	2	)2	+ (σ	2	− σ	3	)2 + (σ − σ	3	)2	= σ	.	(6.39)
1				2		1							1				Т

Выражение для энергии формоизменения (6.37) с точностью до постоянного множителя совпадает с выражением для касательного октаэдрического напряжения:

τ		=	1	(σ − σ		)2	+ (σ		− σ				)2	+ (σ − σ		)2	,	(6.40)
	окт		3	1	2			2				3		1	3
т. е.										3 1 +ν
							Uф	=						2
														τокт .				(6.41)
										2		E

Поэтому Р. Мизес (1913 г.) в качестве критерия предельного состояния при наступлении условий текучести принял величину касательного напряжения на октаэдрической площадке C = τокт и с учетом того, что при осевом растя-

жении в предельном состоянии (σ 1=σ Т , σ 2= σ 3= 0 ):

τ	окт	=		2	σ
				3		Т
получил аналогичное условие пластичности в форме уравнения (6.39).
В условиях чистого сдвига (σ1 = τТ , σ2 = 0							,	σ3 = −τТ ) теория Треска–Сен–
Венана (6.35) дает:
τ Т		σ Т		= 0,5			,	(6.42)

а теория Губера – Мизеса (6.38):

	τ	σ =	1	≈ 0,577 .	(6.43)
			3
	Т	Т

Для большинства конструкционных металлов соотношение (6.43) согласуется с результатами экспериментов лучше, чем (6.42). Наибольшее расхождение имеет место при чистом сдвиге – 15 %. Однако обе теории пластичности получили широкое распространение в практических расчетах.

Критерии разрушения. Критерий максимальных нормальных напряжений.

224

I теория прочности

Предельное состояние разрушения естественно связать с максимальным нормальным напряжением, т. е.

F(σ1, σ2 , σ3 ) = C =		σmax		.	(6.44)

Согласно (6.44), разрушение произойдет в той точке тела, где величина σmax

достигнет определенной для данного материала величины.

При одноосном растяжении σmax = σ1= σ ВР , σ 2= σ 3= 0 , а при одноосном сжатии σmax = σ 3= σ ВС , σ1= σ 2= 0, и тогда условие (6.44) примет вид

F(σ ) = σ

max

= σ

− растяжение

1

ВР

,

(6.45)

F(σ

) =

σ

= σ

− сжатие

3

max

ВС

где σ ВР , σ ВС – пределы прочности материала при растяжении и сжатии.

Критерий максимальных линейных деформаций. II теория прочности

Предельное состояние разрушения при объёмном напряженном состоянии возникнет тогда, когда в данной точке тела максимальная линейная деформация достигнет определенной для данного материала величины. В данном случае переходят к функции деформаций, имеющей тот же смысл, что и

F (σ1,σ2 ,σ3 ):

F(ε1, ε2 , ε3 ) = C = εmax .

(6.46)

При объемном напряженном состоянии:

εmax = ε1 = E1 [σ1 − ν(σ2 + σ3 )],

апри одноосном растяжении:

εmax = σE1 = σEВР ,

отсюда получаем:

225

F(σ1, σ2 , σ3 ) = σ1 − ν(σ2 + σ3 ) = σВР .

(6.47)

Рассмотренные критерии разрушения подтверждаются на практике только для весьма хрупких материалов (стекло, мрамор, гипс) и используются в расчетах на прочность крайне редко.

Эквивалентные напряжения

При проведении расчетов на прочность необходимо знать, при каких значениях напряжений σ1,σ 2,σ 3 функция F (σ1,σ2 ,σ3 ) достигнет своего предель-

ного значения. Для этого необходимы экспериментальные исследования предельного напряженного состояния. Однако комбинаций σ1,σ 2,σ 3 может

быть бесконечное множество, и провести экспериментальные исследования для всех случаев невозможно. Наиболее просто эта задача решается в случае линейного напряженного состояния, т. к. по результатам механических испытаний на осевое растяжение (сжатие) определяются σ Т и σ В .

Поэтому заданное напряженное состояние (объемное или плоское) сводится к эквивалентному линейному напряженному состоянию, описываемому экви-

валентным (расчетным, приведенным) напряжением и которое сопоставляется с предельным состоянием, определенным из эксперимента на осевое растяжение или сжатие (рис. 6.12).

Рис.6.12

Эквивалентные напряжения - напряжения, которые следует создать в растянутом образце, чтобы его состояние было равноопасно с заданным на-

пряженным состоянием. Для определения эквивалентных напряжений используют теории прочности. По результатам экспериментального определе-

ния опасных напряжений (σТ – для пластичных материалов; σВ							– для хруп-
ких и пластичных) устанавливаются допускаемые напряжения
[σ]= σ0 ;	[σ]=	σТ	;	[σ]=	σВ	,	(6.48)
n		n			n
		Т			В

226

где nТ = 1,2 ... 2,0 − коэффициент запаса по пределу текучести σ Т , n В = 1,8 ...

3,0 − коэффициент запаса по пределу прочности σ В .

Эквивалентные напряжения для рассмотренных теорий пластичности и разрушения и соответствующие условия прочности определяются формулами

σэквI = σ1 ≤ [σ];

σэквII = σ1 −ν(σ2 + σ3 ) ≤ [σ];

σIII	= σ −σ			3	≤ [σ];										(6.49)
экв	1
σIV	=	1	(σ − σ			2	)2	+ (σ	2	− σ	3	)2 + (σ − σ	3	)2	≤ [σ].
экв	2				1							1

Объединенные теории прочности Теория прочности Мора

Теория основана на предположении о том, что прочность при объемном напряженном состоянии не зависит от величины второго главного напряжения

σ 2 . Тогда любое напряженное состояние можно представить одним кругом Мора, построенном на напряжениях σ1 и σ 3 . Предельному напряженному

состоянию соответствует предельный круг напряжений. Для различных напряженных состояний имеем семейство предельных кругов Мора. Огибающая кривая предельных кругов Мора зависит от свойств материала и является его механической характеристикой прочности (рис. 6.13).

Рис. 6.13

Для точного построения огибающей требуется большое число экспериментов при различных напряженных состояниях, что трудно реализовать практически. На практике обычно проводят эксперименты при растяжении и сжатии, определяют опасные напряжения σoр и σoc . Огибающая заменяется ка-

сательной АВ к кругам Мора, построенным по результатам испытаний (рис. 6.14).

Главный круг с напряжениями σ1 и σ2 касается прямой АВ.

227

C′

Рис. 6.14

Установим зависимость прочностных свойств материала от вида напряженного состояния. Из подобия треугольников АВВ1 и АСС1 следует:

BB1	=	CC1	.	(6.50)
AB
		AC
1		1

Как видно из рис. 6.14:

BB1 = 12 (σoс −σ

AB1 = 12 (σoc +σ

oр

oр

), CC1 = 12 [(σ1 −σ3 )−σoр]

), AC1 = 12 [σoр − (σ1 +σ3 )].

Подставляя эти выражения в равенство (6.50), получим:

	σoc −σoр			(σ1 −σ3 )−σoр
		=					,
	σoc +σoр			σoр − (σ1 +σ3 )
	или σ1 −		σoр		σ3	=σoр.
			σ
				oc

Примем отношение опасных (предельных) напряжений при растяжении и сжатии:

σoр = μ ,

σoc

тогда получим:

σ1 − μσ3 =σoр .

(6.51)

228

При этом для хрупких материалов вместо σoр и σoc берутся пределы прочности σu , а для пластичных - пределы текучести σ Т .

Соответствующие расчетные формулы условия прочности запишутся:

По методу допускаемых напряжений:

σэкв =σ1 − μσ3 ≤ [σ]р			,	(6.52)
где
	[σ]
μ =	р	.
	[σ]
	c
По методу предельных состояний:
σэкв = σ1 −μσ3 ≤ R			,	(6.53)

где R – расчетное сопротивление при растяжении.

Данная теория описывает разрушение материалов, имеющих разное сопротивление растяжению и сжатию.

F(σ1, σ3 ) = σ1 −μσ3 = σВР ;μ = σВР 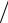σВС ,

где σ ВР , σ ВС – пределы прочности (временное сопротивление) при растяже-

нии и сжатии. Теория дает хорошие результаты для хрупких материалов в случаях, когда круги Мора располагаются между кругами сжатия и растяжения.

Критерий Писаренко-Лебедева

Г. С. Писаренко и А. А. Лебедев, считая, что наступление предельного со-

стояния обусловлено способностью материала оказывать сопротивление как касательным, так и нормальным напряжениям, предложили искать кри-

терий прочности в виде инвариантных по отношению к напряженному состоянию функций касательных напряжений и максимального нормального напряжения.

В этой связи в основу критериального уравнения положены IV и I теории прочности:

μσIV	+ (1−μ)σI	≤ [σ]	; μτ	экв	+ (1−μ)σ	max	≤ σ	вр
экв	экв	p

229

μ =	[σ]p	; σIV =	1	(σ − σ )2 + (σ			− σ )2 + (σ − σ )2 = σ				(6.54)
			2
	[σ]c			1	2	2	3	1	3	i
		экв

σэквI = σ1

μσ1 + (1−μ)σ1 ≤ [σ]р .

Когда материал находится в пластичном состоянии [σ ]p =[σ ]c , μ = 1 , и ус-

ловие (6.54) преобразуется в IV теорию прочности. Для хрупких материалов, когда μ= 0 , получаем I теорию прочности.

Условие прочности (6.54) хорошо согласуется с данными экспериментов для широкого класса конструкционных материалов.

Контрольные вопросы к разделу 6

1. Что называется напряженным состоянием в точке тела?

3. Какими компонентами напряжений характеризуется напряженное состояние в точке? Каково их число?

5.Какие площадки и напряжения называются главными?

6.Какое напряженное состояние в точке деформируемого тела называется линейным, плоским или объемным?

7.Как определяются напряжения на произвольной площадке при плоском напряженном состоянии?

8.Запишите обобщенный закон Гука для изотропного материала.

9.Какими компонентами деформаций характеризуется деформированное состояние в точке тела?

10.В чем состоит прямая и обратная задачи теории упругости?

11.Каким образом связаны между собой три упругие константы материала?

12.Как определяются главные напряжения и положения главных площадок при помощи круга Мора?

13.Что такое эллипсоид напряжений?

14.Охарактеризуйте основные экспериментальные методы определения напряжений и деформаций.

15.Поясните принцип действия механических тензометров, датчиков омического сопротивления.

16.Сформулируйте основные теории прочности.

17.Что такое эквивалентные напряжения?

230

Раздел 7 Расчеты при сложном сопротивлении

Тема 7.1 Косой изгиб

Основные понятия

Впредыдущих разделах курса СМ были рассмотрены простейшие виды нагружения бруса: осевое растяжение и сжатие, сдвиг, кручение и прямой изгиб. В реальных условиях элементы конструкций часто подвергаются воздей-

ствию различных комбинаций простых нагружений. Такие случаи называют сложным сопротивлением.

Под сложным сопротивлением бруса деформированию понимают такие сочетания простых нагружений, когда в его сечениях одновременно возникают несколько внутренних силовых факторов.

Воснове расчетов на сложное сопротивление лежит принцип независимости действия сил, согласно которому напряжения и деформации, вызванные комбинацией силовых факторов, определяются как сумма (алгебраическая или геометрическая) напряжений и деформаций от каждого фактора в отдельности. Данный принцип применим во всех случаях, когда рассматриваются малые деформации в пределах справедливости закона Гука.

Рассмотрим основные виды сложного сопротивления: косой изгиб, внецен-

тренное сжатие (растяжение), изгиб с кручением.

Плоский и пространственный косой изгиб

В случае прямого изгиба силовая плоскость совпадает с одной из главных плоскостей инерции, например – yOz (рис 7.1, а). При этом силовая линия (с.л.) и нейтральная линия (н.л.) взаимно перпендикулярны, а изогнутая ось балки лежит в силовой плоскости.

Нормальные напряжения в случае прямого изгиба вычисляются по формулам

σ =	M x	y и	σ =	M x	.	(7.1)
	Jx			Wx

Косой изгиб – вид нагружения бруса, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей сечения. При этом изогнутая ось балки – плоская кривая, не совпадающая с силовой плоскостью.

Если косой изгиб вызван нагрузками, действующими в одной плоскости (силовой), то изгиб называют плоским (рис.7.1,б). Если нагрузки действуют в разных продольных плоскостях, то это сложный, или пространственный изгиб (рис. 7.1, в). Изогнутая ось балки – не плоская кривая.