u-lectures сопромат

181

ную нагрузку интенсивности qi. Cила QQi представляет собой сумму всех сил левее i-го участка и силы Рi:

j=i

QQi = ∑Pj

j=1

j=i−1

+∑q j lj .

j=1

Момент MМi есть сумма моментов от нагрузки левее i-го участка относительно первого сечения i-го участка и момента Мi.

j=i	j=i−1	k =i−1		j=i−1	k =i−1	l
							j
MMi = ∑M j + ∑ Pj ∑lk				+ ∑ q j lj ∑lk +				.
						2
j=1	j=1	k = j		j=1	k = j+1

Теперь нетрудно записать формулы для поперечных сил Qy и изгибающих моментов Мx в текущем сечении i-го участка (рис. 5.40), удалённом от начала участка на расстоянии zi:

								q z2
Q	= QQ + q	z ,	M	x	= MM	i	+ QQ z +	i i	(5.66)
y	i i	i					i i	2

Подставляя значения нагрузок реальной балки, можно получить для неё по (5.66) значения Qy и Мx.

Необходимо заметить, что при расчёте двухопорных балок нужно положить Р1=P1+RA. Этим сохраним унифицированную схему нагружения, возможность выделить i-й участок как отдельную балку и использовать (5.66) для всех балок.

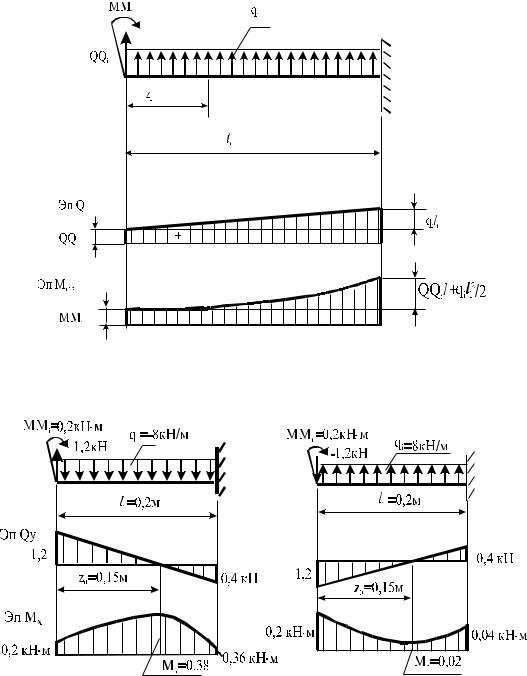
При унифицированном представлении можно изобразить общий вид эпюр поперечных сил Qy и изгибающих моментов Мx, (для консольной см. рис. 5.38, для двухопорной балки − рис. 5.39). Подставляя значения нагрузок реальной балки, можно получить для неё эпюры.

Выполним вычисление поперечных сил и изгибающих моментов на примере левой балки, изображённой на рис. 5.41. Здесь QQ = 1,2кН, MM = 0,2кН·м, q = -8кН/м, l = 0,2м, поэтому в текущем сечении балки по (5.66)

	Qy	=1,2 +(−8) z , M x = 0,2 +1,2 z +(−8) z2 / 2 ,
при	z = 0 Qy =1,2	кН, M x = 0,2 кН·м;
при	z = 0,2м Qy = −4 кН, M x = 0,36 кН·м.

182

Рис. 5.40 Общий вид i-го участка балки

Рис. 5.41 Примеры эпюр поперечных сил и изгибающих моментов

Откладывая от базисной линии на рис. 5.41 полученные значения, изобразим эпюры поперечных сил Qy и изгибающих моментов Мx.

На эпюре Qy наклонная прямая пересекает базисную линию в сечении с абсциссой z0. В этом сечении Qy = 0, а изгибающий момент принимает экстремальное значение Мэкс, и нужно уточнить эпюру моментов. Вычислим по

(5.66) значения z0.и Мэкс :

z0=		QQi / qi		=1,2/8=0,15м, Мэкс=0,2 +1,2 z0 +(−8) z0	2 / 2 =0,38кН·м.

183

Отложив это значение, изобразим перегиб на эпюре моментов (рис. 5.41), соответствующий пресечению наклонной линии на эпюре сил.

Отметим особенности эпюр внутренних усилий, которые хорошо прослеживаются на унифицированной схеме балки.

1.В сечении, где приложена сосредоточенная сила P, на эпюре поперечной силы Q будет скачок по направлению этой силы и на её величину, а на эпюре моментов М – перелом, направленный в сторону действия силы, если эпюра М построена на растянутом волокне.

2.В сечении, где приложен сосредоточенный момент М, на эпюре поперечной силы Q нет изменений, а на эпюре моментов будет скачок на его величину, направленный вниз при взгляде «слева – направо» для положительного момента

М.

3.Чем больше по величине поперечная сила Q, тем круче линия, ограничивающая эпюру моментов М.

4.На участке, где имеется распределённая нагрузка, поперечная сила Q изме-

няется по линейному закону, а изгибающий момент – по квадратичной зависимости (т.е., по кривой 2-го порядка, по параболе), причём тангенс угла наклона эпюры моментов равен Q. Эта особенность является хорошей демонстрацией теоремы Д.И Журавского:

dMx 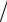dz =Qy , dQy 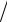dz =qy .

Напомним, что угол наклона эпюры моментов – это угол между касательной к линии, ограничивающей эпюру моментов, и осью бруса.

Тема 5.3 Особенности расчета балок при изгибе

Балка равного сопротивления изгибу

Балка равного сопротивления изгибу – это такая балка, для которой отноше-

ние изгибающего момента M x к осевому моменту сопротивления Wx остается постоянным по всей длине балки

σ = M x = const .

(5.67)

Wx

Так как значение изгибающего момента M x изменяется вдоль балки, то для выполнения условия (5.67) необходимо, чтобы Wx ≠ const . Отметим, что закон изменения M x зависит от вида нагрузки, поэтому находить функцию Wx (z) нужно для конкретной балки.

184

Пусть на консоль действует сосредоточенная сила P . Изгибающий момент будет M x = P z , а напряжение тогда

	σ =	M x =	P z	=		P	= C ,
			W		W кр
		W
		x	x			x
где W кр	– момент сопротивления круглого сечения B. Тогда
x
Wx (z) =	P z						(5.68)
	C

и балка должна иметь такие размеры сечений, чтобы Wx (z) была линейной

функцией.

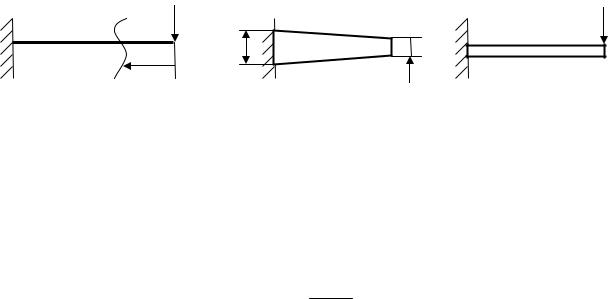
Чаще всего принимают n = const и получают балку, представленную на рис. 5.42, б.

P

B

z

A

а)

P

b b0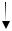

б)

в)

а) нагруженная балка; б) вид сверху; в) фронтальный вид

Рис. 5.42

Переменная ширина изменяется по закону:

b(z) = b0 + b −l b0 z .

Значение b0 определяют из условия среза свободного края балки, а величину

b с помощью выражений (5.67) и (5.68).

Консольная балка равного сопротивления изгибу находит применение при исследовании напряженно-деформированного состояния, т. к. она удобна для тарировки датчиков.

185

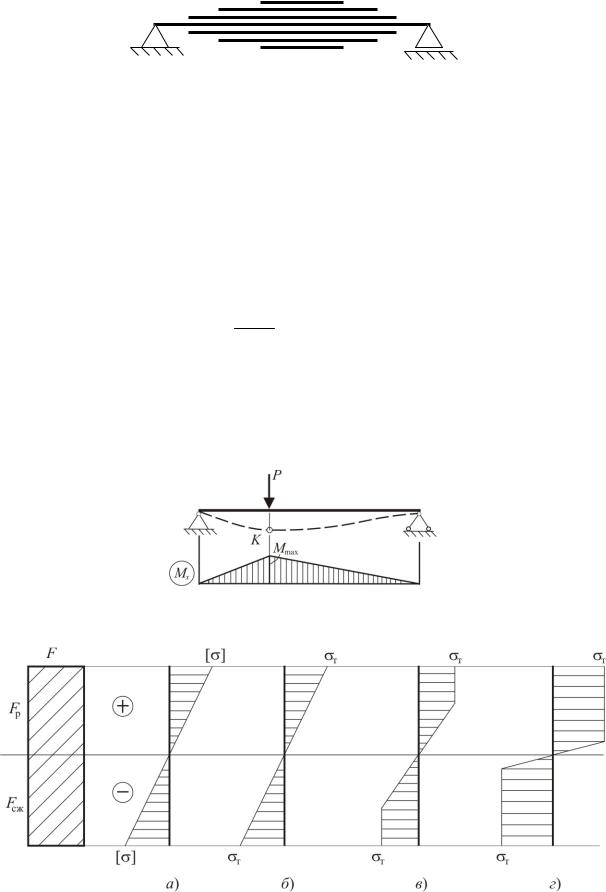
Рис. 5.43

Для других условий и нагрузок можно также найти закон изменения размеров сечения, чтобы соблюсти условие (5.67). Так, например, рессоры в виде положенных друг на друга пластин создают балку равного сопротивления изгибу, если уложены, как представлено на рис. 5.43.

Упруго-пластический изгиб и расчёт по несущей способности

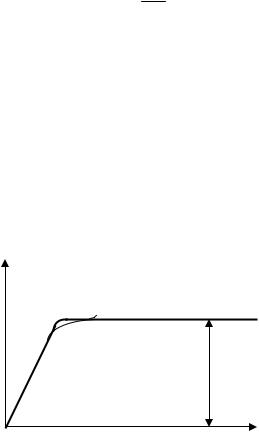
Пусть к балке на 2-х опорах приложена сила P (рис. 5.44). Опасным является

сечение K , в котором σmax = M max , т. к. напряжения σ по сечению изменя-

Wx

ются по линейному закону и σmax возникает в крайних (верхних и нижних)

волокнах балки. Для условия прочности по несущей способности необходимо, чтобы σmax ≤ [σ] (рис. 5.45, а). Рассмотрим возможную работу балки при

дальнейшем увеличении силы P .

Рис. 5.44

186

Рис. 5.45

Сначала σmax = σт возникнет в крайних волокнах (рис. 5.45, б), далее текучесть распространяется вглубь сечения и при возникновении σт практически

по всей высоте сечения (рис. 5.45, г), балка получает возможность резкого поворота своих частей вокруг точки K – это явление получило название «пластического шарнира».

Вычислим изгибающий момент Mпл , в момент образования пластического шарнира.

M пл = ∫σт	ydA + ∫σт			∫ydA +		= σт (Sx− + Sx+ ),
		ydA = σ	т		∫ ydA
Fсж	Fраст		Fсж		Fраст

где Sx− и Sx+ – статические моменты частей сечения с положительным и отрицательным напряжением σт . Сумма (Sx− + Sx+ ) характеризует пластические качества сечения и является пластическим моментом сопротивления Wпл :

(Sx− + Sx+ )=Wпл .

Например, для прямоугольного сечения

Wплпр = bh2 h4 + bh2 h4 = bh42 ,

при этом

Mплпр = σт Wплпр = σт bh42 .

Сравним Mпл с опасной величиной момента, соответствующего опасному моменту метода допускаемых напряжений M т = σт Wx ,

для прямоугольника	W	пр		bh2	4	=1,5 ,
	пл		=
				bh2	6
	Wx

для круга это соотношение будет 1,7 , для двутавра – 1,15. Видно, что полное исчерпание прочности балок происходит при образовании пластического шарнира и при этом разрушающие моменты существенно больше, чем по расчету по допускаемым напряжениям. Это состояние балки называется пре-

187

дельным состоянием и соответствующая ему нагрузка носит название предельной или разрушающей Pпр .

Расчет по предельным нагрузкам более плотно использует несущую способность, поэтому экономически более выгодный. Этот способ расчета называется расчетом по несущей способности (или по предельному состоянию, или по разрушающим нагрузкам). Методика расчета предполагает отыскание пре-

дельной нагрузки Pпр через M xmax (согласно эпюре M x ) и далее расчет предельно допускаемой нагрузки [Pпр]:

[Pпр]= P[nпр],

где [n] – нормативный коэффициент запаса прочности, который устанавливается таким образом, чтобы напряжения при предельнодопускаемых нагрузках были меньше предела текучести σт .

Схематизация диаграммы напряжений

Расчет по несущей способности применим только для конструкций из пластичных материалов. Остановимся на диаграмме напряжений (рис. 5.46).

σ

A B

	σт≈σпц
O	ε

Рис. 5.46. Диаграмма Прандтля

Так как при расчете учитывается текучесть материала конструкции и несущая способность будет считаться исчерпанной, когда произошло течение всего поперечного сечения, то за площадкой текучести дальнейшие участки диаграммы теряют смысл и диаграмму изображают условно виде ломаной прямой OAB (рис. 5.46). Эта диаграмма получила название – диаграмма Прандтля (по имени предложившего её немецкого ученого). При этом материал называют идеально упруго-пластичным.

188

Балка на упругом основании

Многие реальные конструкции (рельсы, резервуары, трубопровод, ленточный фундамент и др.) опираются нижней поверхностью на основания, которые не остаются жесткими, а деформируются. Для таких конструкций введена особая расчетная схема – балка на упругом основании (рис. 5.47).

q

балка

упругое

основание

z r(z)

Рис. 5.47

При нагрузки в упругом основании возникает непрерывно рассматриваемая реакция. Чаще всего основание считают вилклеровским (по имени ученого Э. Вилклера, предложившего эту схему), для которого реакция r в каждой точке основания пропорциональна прогибу v = v(z):

r = k v b,

где b – ширина балки,

k – коэффициент жесткости упругого основания (или коэффициент Постели), который определяется опытным путем, например, для рыхлого песка

k =1–5 МН/м3.
При расчетах в качестве неизвестной принимается функция прогиба v(z), по-
лучив которую, определяют внутренние усилия M x и Qy по формулам
M		x	= EJ		d 2v(z)		,	(5.69)
					dz2
Q	y		= EJ	d 3v(z)		.		(5.70)
					dz3
Учитывая нагрузку q								и реакцию r , запишем суммарную нагрузку в виде

P = q − r . Известно, что интенсивность распределенной нагрузки и поперечная сила связаны дифференциалом:

P = dQdzy .

189

С учетом формул (5.69) и (5.70), получим выражение

	′′	″			(5.71)
	(EJ v (z)) = P = q − k b v(z)
	или при EJ = const
			vIV (z) + 4β4v(z) =	q	,
				EJ
	где β = 4	kb	. Уравнение (5.71) – это дифференциальное уравнение изгиба
		4EJ

балки на вилклеровском основании. Решением этого уравнения является сумма общего v1 и частного решения v2 : v = v1 + v2 . Общее решение выбираем

из математического уравнения, а частное зависит от вида правой части уравнения (5.71). Постоянные определяются из граничных условий. На практике рассматривают расчеты бесконечной, полубесконечной и короткой балки. Также, существуют и другие модели основания.

Остаточные напряжения

Пусть балка нагружена до появления пластического шарнира (рис. 5.48).

Рис. 5.48

В балке возникает момент Mпл . Выясним, что происходит с напряжениями при снятии нагрузки с балки. Эффект снятия можно воспринимать как воз-

190

действие нагрузки противоположного знака, при которой дополнительно возникают напряжения

σсж =	M max	=	σтWпл .
max	Wx		Wx

Эти напряжения показаны на рис. 5.48, б.

При снятии нагрузки исчезают упругие деформации и напряжения (рис. 5.48, б). Практически, происходит алгебраическое сложение напряжений (рис. 5.48, а и б) и в итоге получаем график напряжений (рис. 5.48, в). Эти напряжения называются остаточными.

σA = σт + σсж = σт +		σтWпл = σт	(Wx −Wпл ).
ост	max	Wx	Wx

Для прямоугольного сечения согласно этой формуле будем иметь:

σ	A	= σ	т	(bh2 6 −bh2 4)				= −	σ	т .
	ост			bh	2
						6			2

Предельное состояние и условие прочности по несущей способности

Условимся под предельным состоянием понимать момент исчерпания несущей способности конструкции. Здесь нужно заметить, что к настоящему времени в расчетной практике строительных конструкций (работы профессоров Н. Стрелецкого, А. Гордеева и др.) рассматриваются два других предельных состояния: по развитию чрезмерных деформаций и по раскрытию трещин.

Выше шла речь о предельном состоянии статически определимых балок и приводилась общая методика расчета по несущей способности. Теперь рассмотрим статически неопределимые балки (рис. 5.49). Для такой балки нужно построить эпюру изгибающих моментов M x (рис. 5.49, а).