u-lectures сопромат

121

Поясним вычисление углов закручивания на примере (см. рис. 4.24). Свободный край вала получил угловую деформацию, равную углу закручивания всего вала, который найдём по (4.36):

ϕ11=Δϕ=	1	(1,2 0,2 +(−8) 0,22 / 2) =	0,08	.
	G JR
			G JR
			i

Заметим, что наклонная прямая на эпюре Мк пересекает ось на расстоянии z0 от начала участка. В этом сечении Мк=0, а значение угла ϕ экстремально. Найдём величину z0 по (4.35):

	z0 =		MM i		=	12	= 0,15 ,
			qi			80

и угловую деформацию всего участка z0 по (4.36):

Δϕ0=

(MMi z0 +mi z0

2

2)

=

1

(1,2 0,15 +(−8) 0,152 / 2) =

0,09

.

G JR

G JR

G JR

i

Значение экстремального угла ϕэ в сечении z=z0

равно разности

ϕэ=ϕ11-Δϕ0= =

0,8

−

0,9

= −

0,1

G JR

G JR

G JR

Откладывая полученные значения, изобразим на рис. 4.23 для рассматриваемого вала эпюру ϕ.

Подводя итог рассмотрения унифицированной схемы вала, можно отметить простоту вычислений и построения эпюр.

Расчеты на прочность

Полярный момент сопротивления для круга и кольца соответственно (рис. 4.20, а, б):

Jρ =	πd 4	и	Jρ =	πd 4	(1−α4 ) ,	(4.37)
	32			32

где α = Dd .

122

Рис. 4.23

Тогда моменты сопротивления для сплошного сечения (рис. 4.23, а):

	Wρ =	Jρ		=	πd 3	,	(4.38)
		d	2		16

для кольцевого сечения (рис. 4.23, б):

	Wρ =	Jρ	=	πD3	(1−α4 ) .	(4.39)
		d 2		16

При проектировании валов машин и механизмов расчет ведется по допускае-

мым напряжениям:

τmax =	M z	≤[τ] ,	(4.40)
	Wρ

где M z – нормативный крутящий момент без учета перегрузок; [τ ] – допус-

каемое напряжение материала.

При подборе сечения вала из (4.40) выражают требуемый момент сопротивления:

Wρ = M[τ]z ,

затем в соответствии с (4.38) или (4.39) находят требуемый диаметр, например, сплошного вала:

d ≥ 3 16M z .

π[τ]

123

Условия (4.37) и (4.40) позволяют решать три основные задачи прочности: проверка прочности, проектный расчет и определение несущей способности. Остановимся на сравнительной оценке валов сплошного и кольцевого (полого) сечения. Из эпюры τ для сплошного сечения (рис. 4.23, а) видно, что материал вблизи оси мало нагружен и удаление его снижает затраты материала, облегчает вес вала, при этом τmax возрастает незначительно.

Если валы равнопрочны, то вес полого вала почти в два раза ниже веса сплошного. Это свидетельствует о рациональности применения полых валов, что широко используется в моторостроении.

Определение углов закручивания. Расчет на жесткость

Из соотношения (4.31) находим:
dϕ =	M z dz	,	(4.41)
	GJρ

где GJρ – жесткость сечения при кручении.

После интегрирования (4.41) получим взаимный угол закручивания двух сечений, расположенных на расстоянии l.

	l	M z
	ϕ = ∫		dz .	(4.42)
	0	GJρ

Если на участке M z = const и GJρ = const , то после интегрирования получаем в радианах:

ϕ =	M z l	.	(4.43)
	GJρ

Полный угол закручивания вала определяется суммированием по участкам.

Для оценки жесткости вала используют относительный угол закручивания

( θ), который является мерой деформации при кручении. Из (4.41) получаем:

θ =	M z	.	(4.44)
	GJ ρ

Условие жесткости вала:

124

θ =			M z					≤[θ]		(4.45)
			GJρ
или
θmax =		M z					180		≤[θ] ,	(4.46)
	GJρ							π

где θmax – наибольший относительный угол закручивания, рад/м; θ0max – то же, град/м; [θ ] – допускаемый относительный угол закручивания, зависит от назначения вала и обычно лежит в пределах [θ 0 ]= 0,15 ... 2 град/м.

Выражения (4.45) и (4.46) служат для непосредственной проверки жесткости вала, проектного расчета и определения допускаемого крутящего момента. При подборе сечения вала из (4.45) или (4.46) выражают момент инерции:

Jρ = GM[θz] ,

затем с учетом (4.35) находят требуемый диаметр, например, сплошного сечения:

d ≥	32M z	.
	πG[θ]

Из двух диаметров вала, полученных из условия прочности (4.40) и из условия жесткости (4.45), принимается большее значение.

Потенциальная энергия при кручении

Для определения характеристик прочности и изучения характера разрушения проводят испытания на кручение образцов из различных материалов.

Для пластичных материалов диаграмма кручения подобна диаграмме растяжения (тема 2.3). Работа, затрачиваемая на кручение в пределах упругих деформаций, равна количеству потенциальной энергии, накопленной в брусе, и вычисляется как площадь треугольника на диаграмме кручения.

W =U = 12 M z ϕ.

С учетом (4.43) имеем:

125

		M 2	l
	U =	z		.	(4.47)
		2GJρ
	Анализ напряженного состояния и разрушения при кручении
	При кручении касательные напряжения τ		возникают как в поперечных, так и

в продольных сечениях, а элемент бруса испытывает чистый сдвиг. При чистом сдвиге по площадкам, наклоненным под 45º к оси бруса, действуют растягивающие и сжимающие нормальные напряжения σ (рис. 4.3.)

Поэтому характер разрушения вала будет зависеть от способности материала сопротивляться действию τ и σ.

Трещины разрушения деревянного вала ориентированы вдоль образующей, т.к. древесина плохо сопротивляется τ вдоль волокон (рис. 4.24, а).

Если материал плохо сопротивляется растяжению (например, чугун), то трещины разрушения пойдут по винтовым линиям, касательные к которым образуют угол 45º с осью бруса (рис. 4.24, б).

Рис. 4.24

Стальные валы разрушаются по поперечному сечению от касательных напряжений (рис. 4.24, в).

Статически неопределимые задачи при кручении

126

Методику раскрытия статической неопределимости при решении задач на кручение разберем на примере статически неопределимого ступенчатого вала, нагруженного внешними скручивающими моментами.

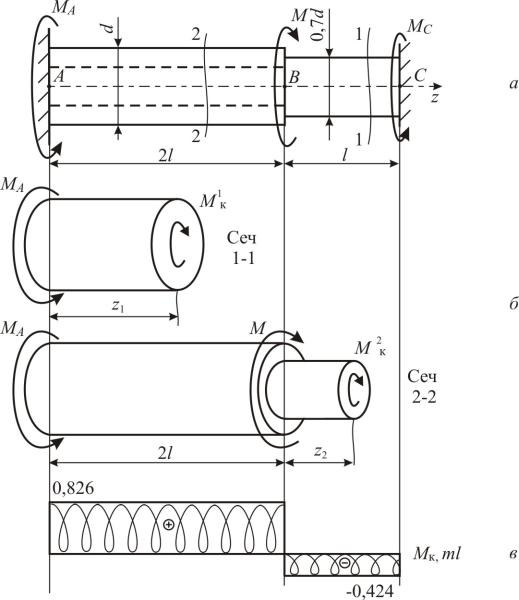
Пример 4.1 Стальной ступенчатый вал заданной конфигурации имеет жёсткие защемления с торцов. Известны внешние скручивающие моменты: M =1,25 ml , m =1,2 кН·м/м; длина l = 0,2 м.

Требуется: Используя уравнение равновесия и уравнение перемещений, найти величины реактивных моментов, возникающих в жёстких заделках и построить эпюру крутящих моментов Mк.

Решение:

1. Нахождение реактивных моментов.

Обозначим реактивные моменты, возникающие в жёстких заделках, как M A и M C (рис. 4.25, а). Их величины должны удовлетворять уравнению равновесия всего вала, которое при кручении записываем по (4.24) как

M A − M + M C = 0

(4.48)

Как видно, это уравнение содержит два неизвестных M A и M C , поэтому вал является статически неопределимым. Для нахождения M A и M C необходимо

составить еще одно уравнение – уравнение перемещений. При кручении уравнение перемещений записывают через углы закручивания участков ϕ. Данный вал состоит из двух участков, поэтому

	ϕ1 +		ϕ 2 = 0,		(4.49)
	где выражения (4.41) для ϕ 1	и	ϕ 2 при M к = const		по участку вала прини-
	мает вид	M к l
	ϕ =			,	(4.50)
		GIρ

где M к – крутящий момент на рассматриваемом участке; G – модуль упругости второго рода или модуль сдвига; Iρ – полярный момент инерции сече-

ния; l – длина участка вала. Для круглого сечения Iρ = π32d 4 , для кольцевого

сечения Iρ = π32d 4 (1 − c4 ), где c = 0,5 – соотношение внутреннего и внешнего

диаметров.

И так, величины реактивных моментов найдём, используя уравнение равновесия (4.48) и уравнение перемещений (4.49).

127

Для участков вала (рис. 4.25, б) из уравнения равновесия отсечённых частей вала найдём выражения крутящих моментов и запишем по (4.50) углы закручивания.

M к1 = M A ; M к2 = M A − M ;

ϕ1

=

M к1 l1

=

M

A

2l

;

ϕ 2 =

M к 2

l2

=

(M

A

− M ) l

.

GIρ1

GIρ 2

GIρ1

GIρ 2

Рис. 4.25

128

Здесь полярные моменты инерции сечения участков принимают значения

	Iρ	=	π d14	(1−c4 )=	π d 4	(1−c4 ); Iρ	=	π d24	=	π (0,7d )4	.
					32					32
		1	32				2	32

Подставляя найденные величины в (4.47), получим уравнение перемещений в виде

M A 2 l 32	(M A − M ) l 32	= 0.
G π d 4 (1 − c4 )+	G π (0,7d )4

Вычислим из этого уравнения реактивный момент M A .

M A 2	(M A − M )	= 0 ,
(1 − c4 )+	(0,7)4

или 2,133 M A + 4,165(M A − M )= 0 ,.. 6,298 M A − 4,165 M = 0, отсюда

MA =4,1656,298M =0,661M =0,6611,25ml=0,826ml=0,826 1,2 103 0,2=198,4 Н м.

Второй реактивный момент можно не вычислять, его значение получится при построении эпюры крутящих моментов.

2. Построение эпюры крутящих моментов.

Подставив найденный момент M A в выражения крутящих моментов по участкам, получим:

M к1 = M A = 0,826 ml =198,4 Н м;

Mк2 = M A −M = 0,826ml −1,25 ml = −0,424ml = −0,424 1,2 103 0,2 = = −101,6 Н м.

Откладывая эти значения от базисной линии на рис. 4.25, в, построим эпюру крутящих моментовM к .

Состояние текучести, понятие о разрушающем моменте и предельном состоянии

Согласно условия прочности при кручении круглого вала наибольшие касательные напряжения τmax возникают у поверхности вала (рис. 4.26, а).

129

Рис. 4.26. Эпюры касательных напряжений

Пусть крутящий момент M K увеличим до опасного значения M т (рис. 4.26, б), при котором τmax достигло предела текучести τmax = τт. У поверхности

вала, выполненного из пластичного материала начнется текучесть. Если и далее увеличивать момент, то текучесть распространится вглубь материала и при достижении разрушающего момента M Р текучесть охватит всё сечение

вала (рис. 4.26, в). Вал достигнет своего предельного состояния, при котором всё сечение подвержено текучести материала и деформация закручивания растет с большой скоростью, вал исчерпает свою несущую способность.

Найдем значение

M р = ∫τт ρdA = τт ∫ρdA = τтWп,		(4.51)
A	A

где Wп = ∫ρdA – пластический момент сопротивления при кручении. Для

A

круглого сечения выделим элементарную площадку dA в виде кольца толщиной dρ и вычислим для круглого сечения WПкр :

кр

d 2

d 2 2

dρ = 2π

ρ3

d 2

=

πd 3

(4.52)

WП

= ∫ρ 2πρdρ = 2π ∫ρ

3

12

0

0

0

кр

=

πd 3

. По-

Сравним эту величину с полярным моментом сопротивления Wx

16

πd 3

лучим увеличение момента сопротивления сечения в

12

=

4

=1,333

раза.

πd 3

16

3

Итак, разрушающий момент для кругло сечения равен

M

р

кр = τ

т

πd 3

12

и

πd 3

больше опасного значения M

т

= τ W кр

= τ

т

16

в 1,333 раза.

т

x

130

Условие прочности по несущей способности

Метод расчета, основанный на понятии разрушающего момента M р , назван расчетом по несущей способности, т. к. при достижении M n вал теряет несущую способность. Значение M р определяется формулой (4.51), при этом для

круглого сплошного сечения Wпкр вычисляется по формуле (4.52), а для кольцевого сечения Wпкольца можем найти интегрированием от dвн 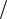2 до d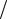2.

Расчет тонкостенных стержней открытого и закрытого профиля

Тонкостенными называют стержни, длина которых значительно превышает размеры поперечного сечения (в 8–10 раз), а в поперечном сечение один размер значительно больше другого (габаритный размер l в 8–10 раз превышает толщину δ) (рис. 4.27).

Рис. 4.27. Примеры тонкостенных стержней

Замечательное свойство таких конструкций в том, что при малом весе они имеют высокую жесткость и достаточную прочность. Благодаря этим показателям такие конструкции широко применяются в технике: элементы мостовых кранов, вагонов, оболочки самолетов, ракет, тележек и т. д.

Основателями теории тонкостенных стержней можно считать С.П. Тимошенко, В.З. Власова.

Тонкостенные стержневые конструкции имеют особую расчетную схему – схему тонкостенного стержня, который рассматривается как брус и при этом формулы сопротивления материалов для внутренних усилий и напряжений применимы для них. Но с другой стороны, в силу геометрических особенностей поперечные сечения имеют особые законы распределения напряжений и деформаций, отличные от классического бруса постоянного сечения и более близкие к теории оболочек.