u-lectures сопромат

31

Рассечем растянутый стержень плоскостью, наклоненной к поперечному сечению под углом α (рис. 2.6, а), и рассмотрим нижнюю часть стержня (рис. 2.6, б). Из условий ее равновесия следует, что напряжения p параллельны

оси бруса, а внутренняя сила pАα , возникающая в сечении, равна F. Здесь Аα - площадь наклонного сечения равная Аα = А/ cosα . Следовательно, pАα = F , откуда

p = F = F cosα = σ cosα,

Aα A

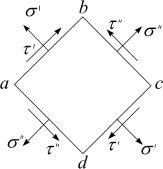
где σ = F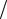 A – нормальное напряжение в поперечном сечении.

Выделим малый элемент в наклонном сечении (рис. 2.6, а,б) и раскладывая р по нормали и касательной к сечению (рис. 2.6, в), находим σα = p cos α и

τα = p sin α. С учетом выражения для р получаем

σα =σ cos2 α,			(2.9)
τα =	1	σ sin 2α.	(2.10)
	2

Следовательно, при растяжении (сжатии) в наклонных сечениях возникают

нормальные и касательные напряжения.

Рис. 2.6

Из формул (2.9) и (2.10) следует:

1. В поперечных сечениях, т.е. когда α =0, имеем

	σα = σmax = σ =	N	; τα = 0.
		A

Нормальные напряжения в поперечных сечениях будут наибольшими, а касательные напряжения равны нулю.

32

2. В продольных сечениях, т.е. при α = 90o, нормальные и касательные на-

пряжения равны нулю:

σα = 0; τα = 0.

Отсюда следует, что продольные слои не испытывают взаимного давления и взаимного сдвига при растяжении и сжатии.

3. На площадках, наклоненных под углом α = 450 , имеем

	τα = τmax =	σ	,	σα =	σ	=	N	,
		2			2		2A

т.е. касательные напряжения будут максимальными, а нормальные напряже-

ния будут им равными.

Следует отметить, что на двух взаимно перпендикулярных площадках касательные напряжения равны по абсолютной величине. Действительно, по формуле (2.10) получаем:

τ(α +90o ) =1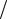2 σ sin(2α +1800 )=1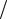2 σ sin(− 2α )= − σ2 sin 2α,

т.е.

τα = −τ(α +90o ).

(2.11)

Формула (2.11) выражает закон парности касательных напряжений: на двух взаимно перпендикулярных площадках, составляющие касательных напряжений, перпендикулярные к общему ребру, равны и направлены обе либо к ребру, либо от ребра.

Этому можно дать наглядное толкование, если из растянутого стержня в окрестности некоторой точки выделить бесконечно малый прямоугольный элемент abcd (рис. 2.6, а), к граням которого приложены напряжения, заменяющие действия отброшенных частей тела (рис. 2.7). Касательные напряжения

τ I и τ II должны быть такой величины и иметь такое направление, чтобы моменты их пар взаимно уравновешивались.

Рис. 2.7

33

Причем для одной и той же точки напряжения различны в зависимости от ориентации секущей площадки.

Условие прочности, три метода и три вида расчётов на прочность

Основные задачи расчетов на прочность:

определение оптимальных геометрических размеров элементов конструкций,

обеспечивающих их прочность;

определение несущей способности, т. е. установление допускаемых или предельных нагрузок, которые может выдержать конструкция, не разрушаясь;

обеспечение способности конструкции удовлетворять заданным эксплуатационным требованиям.

Для решения этих задач разработано три метода расчетов: Расчет по допускаемым напряжениям; Расчет по разрушающим (предельным) нагрузкам; Расчет по предельным состояниям.

Расчет по допускаемым напряжениям

Долгое время, начиная с учения Галилея, господствовало представление о предельной несущей способности конструкции, согласно которому расчет проводился по нагрузкам, соответствующим моменту разрушения. В 1826 г. Навье предложил метод расчета по нагрузкам, реально действующим в эле-

ментах конструкции. Метод основан на определении напряжений от действующих нагрузок и сопоставлении их с допускаемыми. Величина допускаемо-

го напряжения должна составлять некоторую часть от величины напряжений, являющихся опасными (предельными) для материала при данных условиях его работы в конструкции.

Опасными (предельными) напряжениями σlim , τlim называются напряжения от

действия внешних сил, вызывающие потерю несущей способности конструкции, т.е. разрушение или возникновение больших деформаций (limопасное значение, от англ. limit).

Допускаемыми [σ], [τ] называются максимальные напряжения, безопасные для работы конструкции, детали. Действующие в деталях машин и элементов конструкций напряжения σ, τ называют эксплуатационными, в опасных поперечных сечениях они достигают максимальных значений σmax , τmax .

Условие прочности по допускаемым напряжениям предполагает, что напря-

жение в опасном сечении бруса не должно превышать допускаемое:

σmax ≤ [σ],

(2.12)

34

Допускаемые напряжения равны опасным напряжениям σlim , деленным на коэффициент запаса прочности n:

	[σ]=	σlim	,	(2.13)
		n
Для хрупких материалов	(бетон, чугун) за опасные напряжения принимают
предел прочности σlim = σв . Тогда допускаемые напряжения:
при растяжении	[σ]р=			σв
				nв
при сжатии	[σ]c =			σвc .
(2.14)				nв

Для пластичных материалов (низкоуглеродистые, низколегированные стали) за опасные напряжения принимают предел текучести σlim = σТ . Допускаемое

напряжение:	σт .
[σ]=		(2.15)
	nт
Для бетона и железобетона коэффициент запаса по пределу		прочности

nв = 2 − 3,5 ; для древесины nв = 3,5 − 6 для строительной стали Ст3 коэффициент запаса по текучести nт =1,5.

Коэффициент запаса прочности является обобщенным коэффициентом. Необходимость введения коэффициента запаса прочности и его уровни значения определяются:

-статистическим разбросом экспериментального определения предела прочности и предела текучести;

-невозможностью точно установить действующие нагрузки;

-неточностью принятых методов расчета;

-неточностью изготовления;

-качеством металла;

-долговечностью эксплуатации и ответственностью конструкции.

Учет динамического и переменного характера нагрузок для машиностроительных деталей, неопределенность самих нагрузок и неясность их влияния на материал конструкций приводит к необходимости применения повышенных коэффициентов запаса прочности.

Соответствующее условие прочности по допускаемым напряжениям для бруса, работающего на растяжение (сжатие):

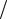
35

	σmax =	N	≤ [σ]	,	(2.16)
		A
	гдеA – площадь сечения бруса (с учетом ослабления),				N – продольная сила в

опасном поперечном сечении бруса. Данное условие позволяет проводить

три вида расчета на прочность:

Проверка прочности (проверочный расчет). Проводят непосредственно по данной формуле (2.16). По известным N и A находят σmax и сравнивают его

с [σ ]. Делают вывод: прочность обеспечена, либо прочность не обеспечена.

Подбор сечения (проектный расчет). По заданным N и [σ ] устанавливают необходимую площадь сечения:

A ≥ N [σ].	(2.17)
Определение несущей способности. По известным	A и [σ ] устанавливают
значение допускаемой продольной силы:
Nдоп ≤ [σ]A.	(2.18)

Расчет по допускаемым напряжениям ведется в пределах упругих деформаций. Применяется при проектировании деталей машин и механизмов.

Продольная и поперечная деформация. Закон Гука. Упругие постоянные материала

Английский ученый Роберт Гук в 1678 г. на основе экспериментов с проволокой и пружинами сформулировал закон “Ut tensio, sic vis”, т.е. “Каково удли-

нение, такова и сила”.

В 1822 г. французский математик Луи Коши ввел понятия напряжение и деформация. В современном виде закон Гука формулируется так:

Относительная продольная деформация прямо пропорциональна соответствующему нормальному напряжению

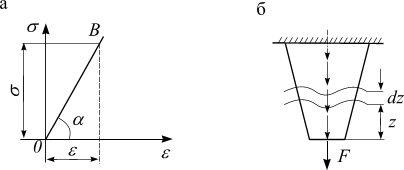
	ε =	σ	,	(2.19)
		E

где E – модуль продольной упругости (модуль Юнга), упругая постоянная материала, характеризующая жесткость материала при растяжении

36

(сжатии); определяется экспериментально, имеет размерность напряжения, например:

для стали Е = 2×105 МПа, алюминиевых сплавов Е = 0,65×105 МПа, для резины E = 7,0 МПа, для дерева Е = 104 МПа, для бетона 0,2 105 МПа.

Идею о модуле упругости впервые высказал в 1800 г. английский ученый То-

мас Юнг. Он же первый указал, что закон Гука справедлив только в пределах упругих деформаций материала.

На рисунке 2.8, а дано графическое представление закона Гука. Установим геометрический смысл модуля упругости Е. Выберем точку В прямолинейного участка ОВ (рис. 2.10,а), координаты этой точки σ и ε .

Рис. 2.8

Очевидно, их отношение (тангенс угла наклона линии ОВ к оси абсцисс) равно модулю продольной упругости :

tqα = σε = E.

Перейдем к определению деформаций стержня. Из формул (2.4) и (2.6) имеем:

l =ε l	и	ε =	N	.
			EA
Тогда абсолютное удлинение участка стержня длиной l при					A = const и
E = const будет равно	Nl
l =		,			(2.20)
	EA

где EA - жесткость поперечного сечения при растяжении (сжатии). Фор-

мула (2.20) выражает закон Гука для абсолютной продольной деформации, ее называют формулой жесткости при растяжении и сжатии.

Если на участке Nz и Az переменны (рис. 2.8 б), то полное удлинение участка l получим, суммируя удлинения бесконечно малых участков dz:

37

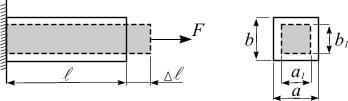
	l	N( z ) dz	.
	l = ∫
		E A( z )
	0

Для бруса, имеющего несколько участков:

	l	N( z )	dz	.	(2.21)
	l = ∑ ∫
		E A( z )
	0
	Удлинение, связанное с температурным воздействием:
	lto = l α		t ,		(2.22)
	где α – коэффициент температурного расширения материала;				t – измене-

ние температуры.

Растяжение (сжатие) сопровождается изменением поперечных размеров (рис. 2.9).

Рис. 2.9

Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:

a = a1 − a ;

b = b1 −b .

Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова:

ε′ = aa = bb .

Между поперечной и продольной относительными деформациями, которые всегда противоположны по знаку, в пределах закона Гука существует постоянное отношение:

ν =		εε′		или ε′ = −νε ,	(2.23)

где ν – коэффициент поперечной деформации (коэффициент Пуассона) –

38

безразмерная величина, упругая постоянная материала, определяемая экспериментально. Для всех изотропных материалов ν = 0 ÷ 0,5. Для пробки ν ≈0; для каучука ν ≈ 0,5; для стали ν ≈ 0,3.

Перемещения. Эпюра перемещений. Условие жесткости

При растяжении (сжатии) поперечные сечения стержня перемещаются в про-

дольном направлении; перемещения поперечных сечений – это следствие де-

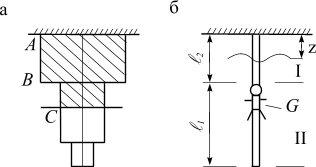
формации. Перемещение сечения зависит от деформации не всего бруса, а лишь части между сечением и неподвижной заделкой. Например, перемещение сечения I-I (рис. 2.10 а) равно деформации заштрихованной части стержня:

δI −I = lAB + lBC , или δI −I = δB + lBC ,

(2.24)

где lAB = δB – деформация участка АВ равная перемещению сечения В; lBC – деформация участка ВС определяется по формулам (2.20) и (2.21).

Но не всегда перемещения сечений какого-то участка непосредственно связаны с его деформацией. Например, по канату, прикрепленному к потолку, на некоторую высоту поднялся человек весом G (рис. 2.10 б). Растягивается (деформируется) только верхняя часть каната, нижняя не деформируется, но перемещается как твердое тело.

I I

Рис. 2.10

С учетом формулы (2.21) для перемещений сечения z можно записать:

δz = ∫	N (z)dz	или	dδz	= N (z)	1	.	(2.25)
	EA
z			dz		EA

Анализируя (2.25), можно сформулировать следующие положения:

На участке, где N (z) = const , перемещение δz – меняется по линейному за-

39

кону;

На участке, где N ( z ) – линейна, перемещение δz – меняется по квадратичной параболе;

Если N ( z ) >0 , то перемещение δz возрастает; N ( z ) <0 , то перемещение δz убывает;

4.В сечении, где N ( z )=δ′z =0, перемещение δz имеет экстремальное зна-

чение: δz = δэкстрем. (максимум или минимум).

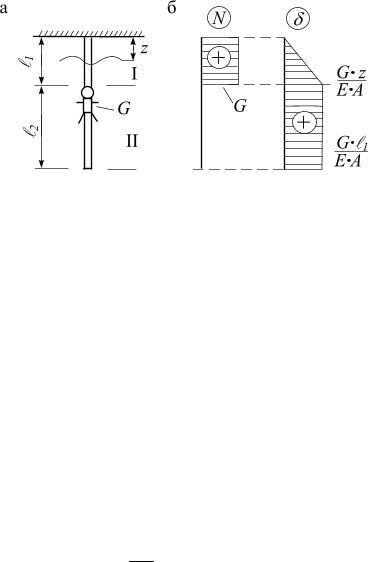
На рис. 2.11 а, б, в показаны: канат под нагрузкой G, эпюра продольной силы и эпюра перемещений. Эпюру перемещений начинают строить от защемленного конца, вычисляя перемещения характерных сечений

					Рис. 2.11
	I участок, 0<z<l1: N1 = G ;			δz =	G z		(линейный закон), при z = l1 переме-
		G l1			EA
	щение δI =		.
		EA				N2 z				G l1
	II участок, 0<z<l2: N2 = 0,			δz = δ1 +				; или	δII =		(const).
										EA
							EA

Для обеспечения нормальной работы конструкций размеры их элементов необходимо выбирать так, чтобы выполнялось условие жесткости, которое со-

стоит в ограничении упругих перемещений:

δ ≤[δ ], или

l≤[δ ].

(2.26)

где δ и l – наибольшее перемещение; [δ ] – допускаемое перемещение.

Для простейшего случая имеем EANl ≤[δ ], откуда

A ≥	Nl			– необходимая площадь поперечного сечения стержня.
	E δ	]
	[

40

Потенциальная энергия упругой деформации

Потенциальной энергией деформации называется энергия, которая накапли-

вается в теле при его упругом деформировании. При разгрузке она расходуется на восстановление первоначальной формы и размеров тела.

При статическом нагружении работа внешних сил W полностью преобразуется в потенциальную энергию U , т.е.

W =U .

(2.27)

На основании закона Гука график зависимости между растягивающей силой F и удлинением l в пределах упругих деформаций представляет собой

прямую (рис. 2.14).

Определим работу силы F на перемещении l.

Пусть при некотором значении силы F1 удлинение бруса равно	l1 . Дадим
силе приращение dF1, тогда удлинение вырастет на величину d	l1 . Элемен-
тарная работа силы F1 на этом перемещении равна
dW = F1d l1

Из рисунка 3.12 видно, что эта величина равна площади узкой заштрихованной полоски графика: dW = dA, поэтому, полная работа

W = ∫dA = A.

пл.A

Таким образом, работа (а значит, и потенциальная энергия) равна площади заштрихованного треугольника

	U =W =	F l	.	(2.28)
		2