u-lectures сопромат

141

Qy = ∫q dz,	(5.8)
l
M x = ∫Qy dz.	(5.9)
l

Интегралы (5.8) и (5.9) есть площади соответственно эпюры внешней распределенной нагрузки q и эпюры поперечных сил Qy на рассматриваемом участке ℓ.

Правила контроля и построения эпюр Q и М

1)На участках, где отсутствует равномерно распределенная нагрузка (q = 0): - эпюра М – наклонная прямая (М изменяется по линейному закону);

- эпюра Q – прямая параллельная оси (Q = const).

2)На участках с равномерно распределенной нагрузкой (q=const):

-эпюра М – квадратная парабола, обращенная выпуклостью в сторону действия нагрузки (построение на сжатом волокне) или вогнутостью в сторону действия нагрузки (построение на растянутом волокне);

-эпюра Q – наклонная прямая (линейный закон).

3) На участках, где

-М алгебраически возрастает слева направо, Q > 0;

-М – убывает, Q < 0;

-М = const; Q = 0 – чистый изгиб.

4)Если на некотором участке эпюра М имеет экстремум, то Q проходит нулевое значение.

Если М – max, то Q от «+» к «-»; если М – min, то Q от «-» к «+».

5)В сечении под сосредоточенной силой:

-на эпюре М наблюдается излом, острие которого обращено в сторону действия силы;

-эпюра Q имеет скачок (по величине и направлению равный силе) 6) В сечении под сосредоточенным моментом:

-эпюра М имеет скачок, равный значению момента;

-эпюра Q – без изменений

7)На концевой шарнирной опоре, где нет внешней пары (m = 0), изгибающий момент М = 0.

8)Изменение М на участке z равно площади эпюры Q на этом участке (следует из выражения (5.9).

9)Изменение эпюры Q на некотором участке z равно площади эпюры q на этом участке (следует из 5.8).

Примеры построения эпюр Q и Мх в простых балках

142

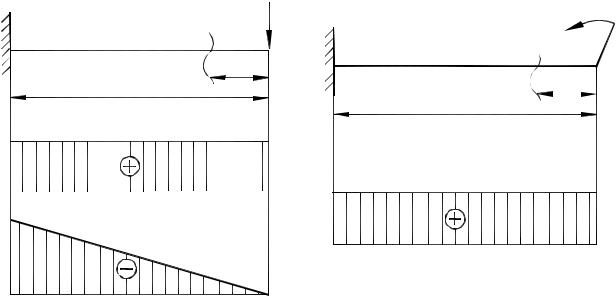
Пример 1. Так называемая балка-консоль, у которой один из торцов защемлен, свободен, подвергается воздействию внешней силы F (рис. 5.6). Построить эпюры Q и Мх.

	F			M
l	z			z
F	F			l
		Q	Q=0
Q			M	M
Fl		Mx

M x

Рис. 5.6

Рис. 5.7

Можно не определять опорную реакцию, если рассматривать нагрузку со стороны свободного конца балки. В нашем примере поперечная сила Q в произвольном сечении с координатой z равна силе F: Q=F, где F учитывается со знаком плюс, поскольку она стремиться вращать отсеченный участок балки по ходу часовой стрелки относительно центра тяжести сечения. Координата z не входит в формулу для Q, поэтому график - горизонтальная прямая (рис. 5.6). Ограничивая эпюру горизонтальной прямой, заполняем ее штриховкой по направлению отсчета ординат.

Изгибающий момент Мх равен произведению силы F на плечо z:

Мх= –Fz,

(5.9)

где принят знак минус вследствие того, что сила F, деформируя балку, вызывает выпуклость ее продольной оси.

В формулу (5.9) для момента Мх входит z в первой степени. График функции Мх = f(z) – наклонная прямая. Чтобы ее провести, достаточно знать положение двух точек на границах балки: 1) при z = 0; Мх = 0, 2) при z = l; Мх = -Fl, где l - заданная длина балки. Строим эпюру Мх сверху, иначе говоря, со стороны растянутых волокон.

143

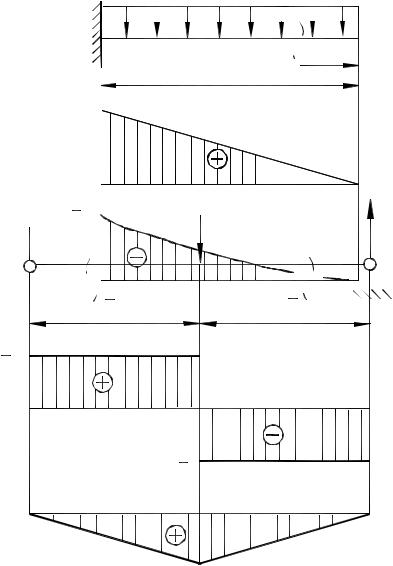
Пример 2. На балку-консоль действует сосредоточенный момент М, (рис. 5.7). Построить эпюры Q и Мх.

Не находя реакции в заделке, опять, же рассматриваем нагрузку справа от произвольного сечения с координатой z. При этом Q = 0, поскольку справа от сечения есть только изгибающий момент М, а силы отсутствуют. Далее определяем:

Мх=М,

(5.10)

где принят знак плюс, поскольку момент М стремится вызвать вогнутость продольной оси балки. Переменная величина z не входит в формулу (5.10) для Мх, поэтому график – горизонтальная прямая. Эпюра Мх пристроена снизу, со стороны растянутых волокон.

Пример 3. На консольную балку приложена равномерно распределенная нагрузка q (рис. 5.8). Построить эпюры Q и Мх. Справа от сечения z нагрузка q действует на участке длиной z. Поэтому сила равна произведению q на z:

Q = qz

ql

Q

ql 2

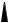R1 2

à Mx

z1 l

Рис.5.11 2

F 2

Q

Mx

(5.11)

q

z l

F	R2

â

l z2

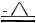
2

F 2

Fl 4

144

Рис. 5.12.

Здесь в правой части – знак плюс, поскольку сила qz стремиться вращать отсеченную часть балки по ходу часовой стрелки относительно центра тяжести проведенного сечения. В формуле (5.11) для Q присутствует z в первой степени, и график Q = f(z) - наклонная прямая. Надо искать положение двух точек на границах балки: 1) при z = 0; Q = 0, 2) при z = l; Q = ql.

Изгибающий момент равен произведению силы qz на плечо z/2. В качестве плеча берется расстояние от сечения z до равнодействующей qz, приложенной посередине участка z. Итак,

Мх= –qz	z	= −q	z2	.	(5.12)
2		2

Знак минус в правой части обусловлен тем, что сила qz вызывает выпуклость продольной оси балки. В формулу (5.12) для Мх переменная z находится в квадрате, поэтому график функции Мх = f(z) – квадратичная парабола. Она вогнута, что соответствует знаку производной dMx/dz. Экстремума нет, поэтому достаточно найти положения в двух точках на границах балки: 1) при z = 0;

Мх = 0, 2) при z = l Мх = – ql2 . 2

Важно отметить, что нет необходимости в поиске промежуточных точек квадратичной параболы, поскольку в расчетах балок на прочность заслуживает внимания только максимальное значение Мх.

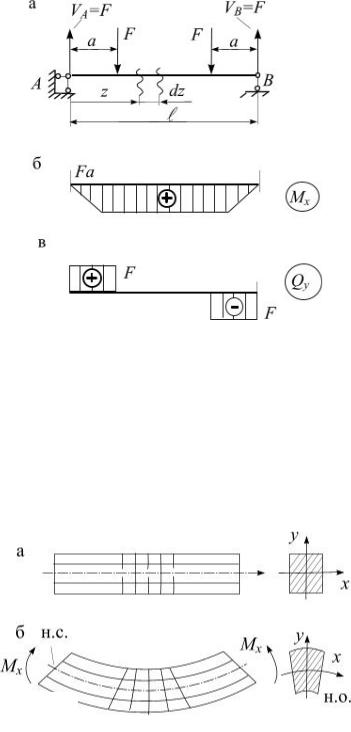
Пример 4. К балке на двух шарнирных опорах приложена внешняя сила F (рис. 5.12). Построить эпюры Q и Мх.

В данном случае горизонтальная реакция на шарнирно неподвижной опоре равна нулю, поэтому она не показана на рисунке. Без поиска реакций R1 и R2 не обойтись. Найдем их из двух уравнений равновесия в моментах всех сил относительно точек a, b:

145

ΣМа(F) = 0,	R2l – F	l			= 0;
	2
ΣМb(F) = 0,	–Rl + F		l		= 0
	2

Отсюда R1 = R2 = F2 .

У балки два участка. Работая на первом участке, где 0 ≤ z1 ≤ 2l , рассмотрим нагрузки слева от сечения. При этом:

	Q = R1 =	F	,	М х= R1z1=	Fz
		2			2

График для Q – горизонтальная прямая, а для Мх – наклонная прямая.

При построении эпюры Мх определяем положение двух точек на границах участка: 1) при z = 0; Мх = 0, 2) при z1= 2l ; Мх= F2l

Переходя ко второму участку, видим, что удобнее рассмотреть все силы справа от сечения z2:

Q = –R =	F	,	М = R z =	F	z
	2			2
2			х 2 2			2

Чтобы провести наклонную прямую на эпюре Мх надо найти положение двух точек на границах второго участка: 1) при z2 = 0; Мх = 0, 2) при z2= 2l ; Мх = F4l .

Уточняем, что знаки плюс и минус в формулах для Q обусловлены уже известными правилами. Сила R1 стремится вращать отсеченный участок балки по ходу часовой стрелки относительно центра тяжести сечения z1, а R2 – против. Изгибающие моменты – положительные на обоих участках, поскольку точки приложения сил R1 и R2 в деформированном состоянии балки выше центров тяжести сечений, и обе силы вызывают вогнутость оси балки. Скачок на эпюре Q под силой F равен силе F.

Пример 5. На балку с двумя шарнирными опорами действует сосредоточенный момент М (рис. 5.13). Необходимо построить эпюры Q и Мх. Определяем опорные реакции R1 и R2. Пишем два уравнения равновесия:

ΣМа(F) = 0, R2l – М = 0,

ΣМb(F)= 0, R1l – М = 0

146

Отсюда R1=R2=			М
			l
			M		R2	R1	q		R2
à				â					â
						à
			2l			z	l
1	z1	l		z2			2
R			3			ql			l
		3
Q						2
						Q
M
l			M						ql
Mx			3			Mx			2
		2M
		3						ql	2
								8
Рис. 5.13						Рис. 5.14

Все процедуры, связанные с построением эпюр Q и Мх аналогичны тем, что рассматривались в примере 4. На левом участке балки имеем:

Q= –R1= – Мl , Мх= –R1z1 = – Мl1 z1 .

при z1 = 0 Мх= 0, при z1	=	l		Мх = – M .
На участке справа:	3				3
					М			Mz2
Q = –R2 = – l						,	Мх= R2z2=
								l
При z2 = 0 Мх = 0, при z2	=		2 l		Мх =	2	М
			3			3

Скачок на эпюре Мх в сечении, где приложен сосредоточенный момент М, со-

ставляет величину М. На самом деле, сверху видим Мх= М3 , снизу – 23М , а в сумме будет М.

147

Пример 6. При равномерно распределенной нагрузке q на балке с двумя шарнирными опорами (рис. 5.14) построить эпюры Q и Мх.

Опорные реакции определяем из двух уравнений равновесия:

ΣМа(F) = 0, R2l –ql		l		= 0,
2
ΣМb(F ) =0, –R1l + ql	l			= 0.
2

Отсюда R1=R2= q2l . Заметим, что плечом силы ql является расстояние от опо-

ры до линии действия равнодействующей нагрузки q, это l/2.

У балки один участок. Поперечная сила Q в сечении равна алгебраической сумме всех сил, приложенных по одну сторону от сечения:

Q = R1	– qz= ql	−qz.	(5.13)
	2

Вычитаемое qz учтено со знаком минус, поскольку нагрузка q на участке z стремиться вращать отсеченную часть балки против хода часовой стрелки относительно центра тяжести сечения. В формуле (5.13) для z находится в первой степени, поэтому график – наклонная прямая. Определяем положение точек на границах балки:

при z = 0; Q = q2l , при z =l; Q= − q2l

Изгибающий момент в сечении равен сумме моментов всех сил, приложенных по одну сторону от сечения.

Мх =R1z– qz22 = q2l z − qz22

Здесь qz есть сила, а 2z – плечо. График Мх – квадратичная парабола. На гра-

ницах балки имеем:

при z = 0 и z = l Мх=0.

Изгибающий момент будет максимальным посередине пролета:

при z=	l	Мх = ql	.	l	− q	(	l	)2	=	ql2	.
2		2	2		2	2			8

Через три найденных точки проводим параболу. Очевидно, что она выпуклая.

148

Чистый изгиб

Рассмотрим балку (рис. 5.15, а), для которой построены эпюры Qy и Мx (рис. 5.15, б, в).

В средней части балки возникает чистый изгиб (Qy = 0, Мx = const). Нанесем на боковой поверхности балки сетку ортогональных линий (рис. 5.16, а).

Рис. 5.15

В результате деформирования на участке чистого изгиба (рис. 5.16, б) можно видеть:

–продольные волокна искривляются по дуге окружности: одни – укорачиваются, другие - удлиняются; между ними есть слой волокон, которые не меняют своей длины – нейтральной слой (н.с.), линию его пересечения с плоскостью поперечного сечения называют нейтральной осью (н.о.);

–расстояние между продольными волокнами не меняется;

–поперечные сечения, оставаясь прямыми, поворачиваются на некоторый угол.

Рис. 5.16

149

Эта картина деформирования позволяет принять следующие допущения:

Оненадавливании продольных волокон друг на друга, т.е. каждое волокно на-

ходится в состоянии простого растяжения или сжатия, что сопровождается возникновением нормальных напряжений σ.

Осправедливости гипотезы Бернулли, т.е. сечения балки, плоские и нормаль-

ные к оси до деформации, остаются плоскими и нормальными к ее оси после деформации.

Нормальные напряжения при изгибе

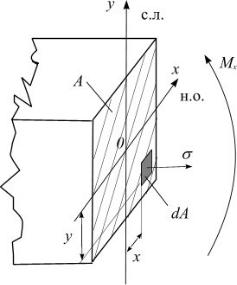
Проведем сечение z (рис. 5.15, а) и в поперечном сечении покажем координатные оси (рис. 5.17), причем ось Оy совместим с силовой линией (линией пересечения силовой плоскости с плоскостью сечения).

Рис. 5.17

При чистом изгибе в сечении балки возникает только изгибающий момент Мx , остальные внутренние усилия равны нулю (N = 0, Мy = 0 и т.д.). Следовательно, на площадке dА будет действовать только напряжение σ, для определения которого рассмотрим три стороны задачи.

Статическая сторона задачи выражается интегральными уравнениями равновесия

N = ∫σ dA = 0,	(5.14)
A
M y = ∫σ xdA = 0,	(5.15)
A

150

M x = ∫σ ydA.	(5.16)
A

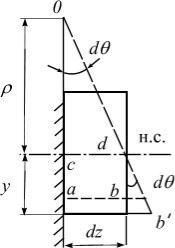
Геометрическая сторона задачи (в основе лежит гипотеза плоских сечений). Выделим элемент dz (рис. 5.15, а) и рассмотрим его деформированное состояние, приняв левое сечение условно за неподвижное (рис. 5.18). В результате поворота правого сечения на угол dθ нижние волокна удлиняются, верхние - укорачиваются.

Нейтральный слой отметим отрезком cd = dz = ρ dθ. Волокно ab = dz получит приращение длины на bb′ = y dθ. Относительное удлинение волокна ab равно

	ε =		bb′	= −	ydθ	= −	y	,
			ab		ρd
							ρ
где ρ – радиус кривизны нейтрального слоя (н.с.);
y – расстояние от волокна до нейтрального слоя.
Геометрическая сторона:
ε = −	y	,				(5.17)
	ρ

т.е. деформация волокна пропорциональна его расстоянию до нейтрального слоя.

Рис. 5.18

Физическая сторона задачи (выражается законом Гука)

	ε =	σ	или σ = ε E .	(5.18)
		E
	Проведем синтез всех сторон. Из выражений (5.17) и (5.18) следует:
			σ = Ey 1 .	(5.19)
			ρ
	Свяжем полученную формулу для напряжений σ = Ey			1	c внутренними уси-
				ρ

лиями.

Подставляя (5.19) в (5.14) и (5.15), определим положение нейтральной оси:

N = ∫	Ey	dA = 0 или	E	∫y dA = 0.
			ρ
A	ρ			A