u-lectures сопромат

51

σ= NA = const → σ = PA+(zqz) = const

инужно найти F(z) . Представим A(z) = A0 + kz . Получим

					q
P + qz		P 1		+			z
					P
	= const или									= const ,
A0 + kz					k
		A	1	+				z
					A
	0
					0

Отсюда придём к соотношениям

k

=

q

и k =

A

q

.

A

P

0

P

0

q

Получаем закон распределения

площади

сечения

A(z) = A

1

+

z (рис.

P

2.21).

0

Рис. 2.21
Отсюда напряжение получим равным σ =		P + qz				= const .
				q
	A	1	+		z
				P
0

2 случай. В массивном стержне (рис. 2.22) площадь поперечного сечения изменяется по закону Az = f (z) . Чтобы учесть собственный вес стержня, пред-

ставим его распределенной нагрузкой интенсивностью q = Az 1 γ (это вес единицы длины бруса).

52

Рис. 2.22

Продольная сила в сечении z

			z							z
	N(z) = P + ∫qz dz = P + γ∫A(z)dz .
			0							0
	Для бруса равного сопротивления σ =				N(z)			= const , тогда имеем
					A(z)
		P + γ∫z		A(z)dz				=		P
			0
											.
			A(z)							A
										0
	Решаем это уравнение, умножив на A(z) ,
	P + γ∫z		A(z)dz =				P		A(z).
	0						A0

Далее проинтегрируем по z :

γ A(z)dz = P d(A(z)),

A0

γA0 dz = d(A(z)). P A(z)

Проинтегрировав последнее выражение, получим

53

∫z γ A0 dz = ln A(z),

0 P

γ PA0 z = ln A(z).

Исходя из свойств логарифма, перепишем формулу в виде

				γA
		A(z)= С e		0		z .
				A
			γA
При	z = 0	, A(z)= C . Значит, A(z)= A e	0		z	– закон изменения площади по-
			A
		0

перечного сечения массивного бруса.

Изготовить такой брус затруднительно, поэтому на практике эту проблему решают либо, используя линейную зависимость (как в случае 1), например, в высоких трубах, либо составляя ступенчатый брус, как для железобетонных фундаментов промышленных колонн.

Тема 2.2. Специальные расчеты статически неопределимых систем при растяжении (сжатии)

Определение температурных напряжений

Температурные напряжения возникают в результате изменения температуры элементов конструкции. Они характерны только для статически неопределимых систем, так как в статически определимые стержни удлиняются беспрепятственно.

Рассмотрим статически неопределимую систему (рис. 2.23, а), для которой возникновение внутренних сил связано с внешним температурным воздействием.

Два жестких горизонтальных бруса соединены тремя стержнями. Крайние стержни изготовлены из стали и имеют площадь поперечного сечения FC ,

средний стержень – медный, FM .

С учетом симметрии системы и равной жесткости крайних стержней, продольные силы в этих стержнях будут одинаковы.

Предположим, что все стержни растянуты (рис. 2.23, б). Тогда уравнение равновесия будет иметь вид:

	∑Fy = NC + NM + NC = 0 ,
2NC + NM = 0 .	(2.36)

54

Рис. 2.23

Система один раз статически неопределима, т. к. другие независимые уравнения равновесия отсутствуют. Для её решения составим дополнительное уравнение.

После повышения температуры на величину t брусья должны оставаться горизонтальными, поэтому абсолютные удлинения всех стержней одинаковы

lC = lM .

(2.37)

Абсолютное удлинение каждого стержня равно сумме его температурного удлинения и упругой деформации от продольной силы:

lM	= αM l t +				NM l		,
				EM FM
l	= α	C	l t +		NCl
C					EC FC

где α – коэффициент температурного расширения (удлинения) соответственно для медного и стального стержней;

E – модуль продольной упругости материала.

Подставим полученные выражения для абсолютных удлинений стержней в равенство 2.37:

αM l t +	NM l	= αCl t +	NCl	.	(2.38)
	EM FM
			EC FC

55

Решая совместно уравнения 2.36 и 2.38, получим выражение для нахождения продольного усилия в стальном стержне

NC = (αM −αС )	t	EC FC			.
		(1+ 2E F )	E	F
		C C		M M

Продольное усилие в медном стержне тогда NM = −2NC .

Так как αM > αC ( αM =167 10−7 1/град, αC = (100 −130) 10−7 1/град), то про-

дольная сила NC будет положительна, следовательно, стальные стержни рас-

тянуты, а медный – сжат.

Температурные напряжения в стержнях будут равны соответственно:

σM = NM и σC = NC .

FM FC

Понятие о монтажных напряжениях

Рассмотрим случай возникновения монтажных напряжений, связанных с неточностью изготовления конструкции.

Стальная конструкция состоит из трех стержней с площадями поперечных сечений F1 , F2 и F3 , концы которых прикреплены к двум абсолютно жестким

плитам (рис. 2.24, а).

Рис. 2.24

56

Все стержни должны были иметь одинаковую длину l , однако, стержень 1 был изготовлен на δ1 длиннее, а стержень 2 на δ2 короче, чем по проекту (от-

носительно стержня 3) (рис. 2.24, а). Заметим, что δ1 и δ2 весьма малы по

сравнению с длиной l . Из-за неточности при изготовлении возникают начальные (монтажные) напряжения. Определим эти напряжения. Предположим, что после монтажа конструкции нижняя плита заняла положение, показанное на рисунке, и все стержни оказались растянуты.

Уравнение равновесия:

∑Fy = N1 + N2 + N3 = 0 ,	(2.39)
∑M A = −N2a − N3 (a +b) = 0 .	(2.40)

Для составления дополнительного уравнения рассмотрим удлинения стерж-

ней при монтаже. Из геометрического подобия

ACE и BCD имеем

h1

= (a +b)

,

h

b

2

при чем, исходя из условия, h1 =

l1 −( l3 −δ1 ), а h2 = l2 −( l3 + δ2 ). Тогда

l1 + δ1 −

l3

= a +b .

(2.41)

l

l

2

−δ

2

−

b

3

Удлинения стержней

l =

N1l

,

l

2

=

N2l

и

l

3

=

N3l

.

1

EF1

EF2

EF3

Подставив данные выражения в пропорцию 2.41 и затем, совместно решая уравнения 2.39 и 2.40, находим значения продольных напряжений в стержнях N1 , N2 и N3 (рис. 2.24, б), а далее и монтажные напряжения в стержнях σ1 ,

σ2 и σ3

На практике такие конструкции могут наблюдаться, например, при создании напряжений в арматуре бетонных конструкциях; в дальнобойной артиллерии

– предварительный натяг, который создает сжимающие напряжения во внутренней части ствола и так далее.

Предельное состояние и расчет по несущей способности

Метод основан на вычислении не напряжений, а нагрузки, которую может выдержать конструкция, не разрушаясь.

Условие прочности предполагает, что максимальная действующая нагрузка

57

Fmax не должна превышать допускаемой нагрузки, полученной путем деления разрушающей нагрузки на коэффициент запаса прочности

F <[F]=

Fразр

.

(2.42)

max nB

Значения nВ принимаются, как и при расчете по допускаемым напряжениям

для хрупкого материала.

В случае пластичного материала критерием предельного состояния является

потеря несущей способности в результате превращения конструкции в кинематически изменяемую за счет неограниченного роста пластических деформаций.

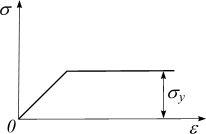
Расчет ведется за пределом упругости с учетом пластических деформаций, где закон Гука не соблюдается. Принимается схематизированная диаграмма напряжений – диаграмма Прандтля с безграничной площадкой текучести (рис. 2.25). Расчет на прочность основан на вычислении предельной нагрузки Flim , которую находят с использованием уравнений предельного равновесия,

поэтому он называется методом предельного равновесия.

					σт
	Рис. 2.25
Условие прочности по предельным нагрузкам имеет вид:
F <[F ]=		Flim	.	.			(2.43)
max		n т

Тема 2.3 Экспериментальное изучение механических характеристик материалов

Испытание образцов различных материалов на растяжение Диаграммы растяжения

При проектировании и расчетах на прочность и жесткость необходимо знать свойства материалов, сведения о которых можно получить путем механических испытаний на растяжение, сжатие, сдвиг, кручение и изгиб.

58

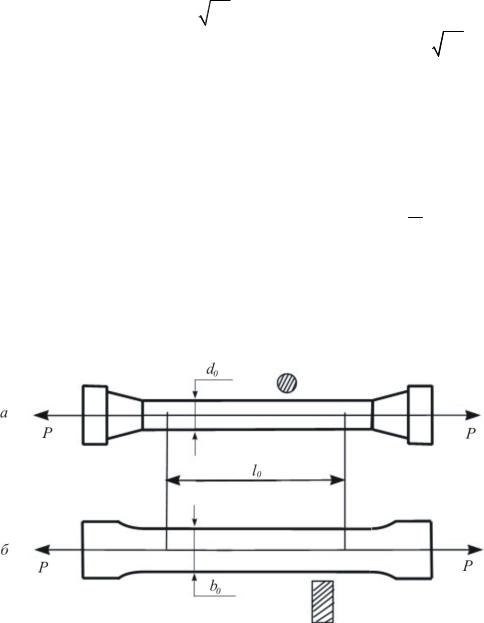
Для испытаний на статическое растяжение черных и цветных металлов и изделий из них согласно ГОСТ 1497-84 (ИСО 6892-84, СТ СЭВ 471-88) применяют цилиндрические образцы диаметром 3 мм и более, а также плоские (из листового материала) образцы толщиной 0,5 мм и более (рис. 2.26, а и б).

Расчетная длина образца l0 =5,65 А0 - для коротких образцов (у цилиндрических l0 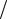d0 = 5), где А0 - начальная площадь образца, и l0 =11,3 А0 - для длинных (у цилиндрических l0 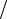d0 =10 ). Согласно принципу Сен-Венана, напря-

женное состояние в рабочей части образца не зависит от способа приложения нагрузки к образцу и может считаться однородным. При одноосном растяжении в образце возникает однородное напряженное состояние, то есть во всех точках поперечного сечения рабочей части образца напряжение получается одинаковым и, независимо от того деформируется образец упруго или пла-

стически, оно вычисляется по одной и той же формуле: σ = PА.

Выбор формы и размеров образца устанавливается возможностями изготовления, а также характеристиками испытательной машины. В целях экономии материала при массовых испытаниях целесообразно проводить испытания коротких образцов.

Рис. 2.26

Испытание на растяжение проводят на специальных разрывных или универсальных машинах, создающих постепенно возрастающую нагрузку на образец. Машины снабжены устройством для автоматической записи диаграммы растяжений, т. е. графика зависимости между растягивающей силой P и удлинением образца l .

59

Диаграмма растяжения малоуглеродистой стали

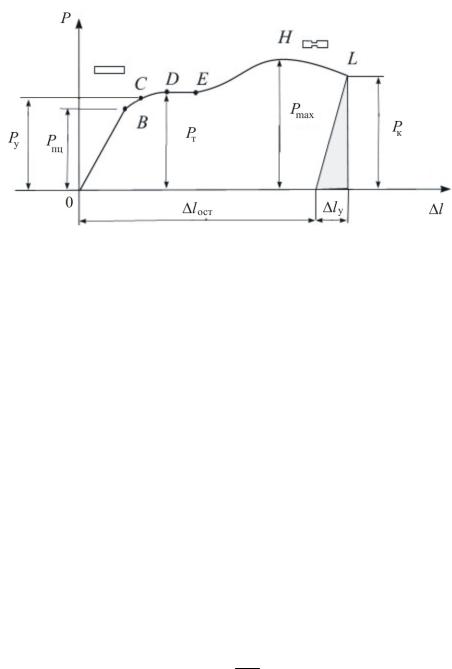
На рис. 2.27 изображена диаграмма растяжения стали марки Ст 3 с содержанием углерода не более 0,22 %. Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца.

Рис. 2.27

Участок ОВ – зона пропорциональности. На этом участке зависимость между удлинением образца и силой носит линейный характер, таким образом, выполняется закон Гука.

σ = Е ε ,

где E (МПа) – физическая константа материала, называемая модулем продольной упругости или модулем упругости первого рода, характеризующая жесткость материала. Значения модуля упругости зависят от типа кристаллической решетки и межатомного взаимодействия и определяются экспериментально.

Прямая пропорциональная зависимость между напряжением и деформацией сохраняется до напряжений, соответствующих пределу пропорциональности σпц, который определяется делением соответствующей нагрузки на началь-

ную площадь образца А0 :

P

σпц = Апц

0

Предел пропорциональности зависит от условно принятой степени приближения, с которой начальный участок диаграммы можно рассматривать как прямую. Степень отклонения кривой σ = f (ε) от прямой σ = Е ε определяют

по величине угла, который составляет касательная к диаграмме с осью σ . В

60

пределах закона Гука тангенс этого угла определяется величиной 1/ E . Обычно считают, что если отношение σ = dε / dσ на 50 % больше, чем 1/ E , то предел пропорциональности достигнут.

Упругие свойства материала сохраняются до напряжения, называемого пре-

делом упругости. Под пределом упругости понимается такое наибольшее на-

пряжение, до которого в образце еще отсутствуют пластические деформации. Для большинства материалов предел упругости совпадает с пределом пропорциональности и их определение во многом зависит от установленных требований точности. Обычно остаточную деформацию, соответствующую пре-

делу упругости, принимают в пределах ε ост = (1...5) 10−5 , т.е. 0,001…0,005%. Соответственно этому допуску предел упругости обозначают σ0,001или σ0,005 .

Участок ОС – зона упругости. Выше точки В диаграмма искривляется, закон Гука нарушается, деформации начинают расти быстрее роста напряжений. На этом участке в непосредственной близости от точки В находится точка С, соответствующая пределу упругости σу :

σу = PАу . (2.44)

0

Пределом упругости называется наибольшее напряжение, до которого остаточная деформация при разгрузке не обнаруживается. Для Ст 3 σу =205 –

210 МПа, т. е. σпц и σу незначительно отличаются, и обычно считают, что они

практически совпадают.

Участок DЕ – носит название площадки текучести. Наличие площадки текучести связано с развитием сдвигов в кристаллической решетке. При возникновении заметных пластических деформаций, поверхность образца покрывается системой тонких линий (полос скольжения). Эти линии, называемые линиями Людерса-Чернова (рис. 2.28), имеют преимущественное направление, составляющее с осью угол, близкий к 45°, и практически совпадают с плоскостями максимальных касательных напряжений.

Рис. 2.28

Напряжение, при котором происходит деформирование образца без заметного увеличения нагрузки, называется пределом текучести. Стрелка силоизмерительного механизма на время останавливается, т.е. образец удлиняется при фактически постоянной нагрузке равной Pт . Соответствующее напряжение

вычисляется по формуле: