u-lectures сопромат

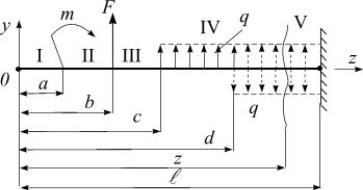
171

сматриваемого участка, продолжать ее до этого конца, уравновешивая противоположно направленной (компенсирующей) нагрузкой, которую показывают штриховыми линиями;

Составлять выражения изгибающего момента М(z), учитывая нагрузки, расположенные левее рассматриваемого сечения, в том числе и реакции опор;

Умножать момент внешней пары m на множитель (z – a)о, равный единице, где а - абсцисса точки приложения m ;

Интегрировать уравнения на всех участках, не раскрывая скобок.

В математике подобное решение дифференциальных уравнений связано с именем французского ученого О.Л. Коши (1789-1857).

Рассмотрим произвольно нагруженную консоль (5.35), где a, b, c, d – абсциссы точек приложения соответствующих нагрузок. Балка имеет пять участков. Помещаем начало координат на левом конце балки. Продолжаем нагрузку q до правого конца и показываем компенсирующую. Составим выражение изгибающего момента на последнем участке с учетом условия 3:

M (z) = m(z − a)o + F(z − b) + q(z − c)2 − q(z − d)2 . 2 2

Рис. 5.35

Подставим его в дифференциальное уравнение (5.53). Вводя в знаменатель сомножитель равный единице, получим:

EJ x y′′(z) = m(z − a)o +	F(z −b)1	+ q(z − c)2	− q(z − d)2
	1	1 2	1 2

Производим двукратное интегрирование:

172

EJ x	y′(z) = m(z − a)1		+ F(z −b)2		+ q(z − c)3	− q(z − d)3	+ C
	1		1 2		1 2 3	1 2 3
EJx y(z) = m(z − a)2 +		F(z −b)3 + q(z − c)4 − q(z − d)4 + C z + D (5.61)
	1 2	1 2 3		1 2 3 4 1 2 3 4

Постоянные C и D определяются из граничных условий в заделке: при z = l угол поворота y′(l)= 0 и прогиб y(l)= 0 . Согласно геометрическому смыслу

постоянных, установленному в примере, рассмотренном выше:

D = EJ x y0 и C = EJ xθ0 ,	(5.62)
где θ0 и y0 – угол поворота и прогиб в начале координат,	называемые в

дальнейшем начальными параметрами.

Подставляя выражения постоянных (5.62) в уравнения (5.61), располагая члены уравнений по возрастающим степеням z и применяя знак суммы для случая многократного повторения однотипных нагрузок, а также факториал в знаменателе, получим универсальные уравнения перемещений при изгибе:

EJxθ(z) = EJxθo	+∑	m(z −a)1	+∑	F(z −b)2	+∑	q(z −c)3	−∑		q(z −d)3	(5.63)
	1!		2!		3!			3!
EJ x y(z) = EJx yo + EJ x θo z + ∑m(z − a)2					+ ∑ F(z −b)3			+
			1!		2!					(5.64)
+ ∑q(z − c)4 −	∑q(z − d)4 .
3!	3!

Из уравнения (5.63) определяют угол поворота θ(z), из (5.64) – прогиб y(z),

где z – текущая координата.

Определение θ и y в различных сечениях с помощью (5.63) и (5.64) носит на-

звание метод начальных параметров. Примечание:

–уравнение углов поворота (5.63) можно получить дифференцированием уравнения (5.64), которое называют универсальное уравнение упругой линии балки.

–полезно запомнить. Из метода сечений (раздел 1) следует, что при составлении выражения М(z) учитывают нагрузки, расположенные по одну сторону сечения z (в нашем случае слева), поэтому:

• при составлении уравнения (5.64) следует учитывать все нагрузки и реакции опор, расположенные левее сечения, при этом выражения (z-a), (z-b)...(z-i) могут быть только положительными;

173

• нельзя включать ни одну нагрузку, приложенную правее сечения. В этом случае (z −i) <0, и такое слагаемое должно быть вычеркнуто из (5.64).

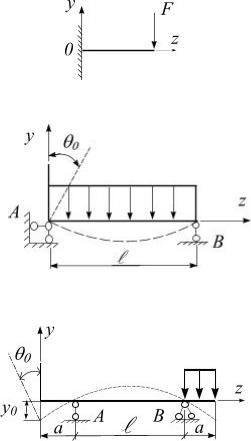
Определение начальных параметров

Начало координат совпадает с заделкой.

	Начальные параметры равны ну-
Начало	лю.
	совпадает с шарнирной опорой.
	Угол поворота в начале координат
	не равен нулю.	y0 = 0 .
	θ0 ≠ 0 ,
	Для определения	θ0 имеем гранич-

ное условие на правой опоре: при z=l,

Начало координат находится на свободном конце.

		Начальные	параметры	отличны	от
		нуля.	θo ≠ 0 , yo ≠ 0 .
	О
		Начальные	параметры	находим	из

граничных условий на опорах:

при z = а, yА = 0;

при z = а+l, yВ = 0.

Порядок расчета по методу начальных параметров

Определяют опорные реакции и проставляют их на расчетной схеме.

Выбирают единое начало координат на левом конце балки и выявляют, равны нулю начальные параметры или нет.

Если нагрузка q не доходит до правого конца рассматриваемого участка, то ее продолжают и показывают компенсирующую.

Записывают универсальное уравнение прогибов (5.64) обычно для последнего участка, учитывая силы левее рассматриваемого сечения. Слагаемые в урав-

174

нении имеют знак изгибающего момента.

Дифференцируют уравнение (5.64) и получают уравнение углов поворота

(5.63).

Если начальные параметры не равны нулю, то их определяют из граничных условий.

Подставляя в (5.63) и (5.64) соответствующее значение z, определяют θ и y в данном сечении.

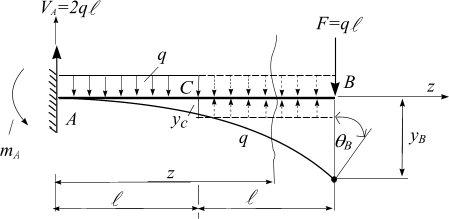
Пример 1. Определить перемещения свободного конца и сечения в середине консоли вылетом 2ℓ (рис. 5.36).

mA=2,5qℓ2

Рис. 5.36

Решение: Определяем реакции заделки:

VA = 2ql, mA = 2,5ql2 .

Помещаем начало координат на левом конце в заделке. Очевидно, начальные параметры равны нулю:

y0 = 0 , θ0 = 0 .

Продолжаем нагрузку q до правого конца балки и прикладываем компенсирующую.

Записываем для последнего участка (СВ) универсальное уравнение прогибов (5.64), учитывая силы, расположенные левее сечения z.

175

EJx y(z) = − m(z −0)2	+ VA (z −0)3	− q(z −0)4	+ q(z −l)4	(а)
2!	3!	4!	4!

Дифференцируя выражение а, получаем уравнение углов поворота:

EJx	θ(z) = − m(z −0)1	+ VA (z −0)2	− q(z −0)3	+ q(z −l)3 .	(б)
	1!	2!	3!	3!

Подставляя z = 2ℓ в (а) и (б), определяем прогиб и угол поворота на конце балки:

EJx yB = − 2,5ql2 (2l− 0)2				+	2ql(2l− 0)3	− q(2l− 0)4	+
		2			6	24	(в)
+ q(2l− l)4		71ql4
	= −		;
24		24

EJ θ		B	= − 2,5ql2 (2l−0)1				+ 2ql(2l−0)2	−
	x				1		2
+	q(2l−l)3			= −	13ql3	.
			6		6

Окончательно из (в) и (г) получаем:

	yB	= −	71ql4	; θB
			24EJx

	q(2l−0)3	+
	6
		(г)

= −13ql3 . 6EJx

Подставляя z = l в (а) и (б) и учитывая силы левее точки С, находим прогиб и угол поворота в середине балки:

		2					l−		3		4								2	2						3		4				4
EJxy(l) =−		m(l−0)		+		VA(			0)		−		q(l−0)		=−		2,5ql			l		+			2ql l			−		ql		=−23ql	,
		2																							6
							6		2		24							2										24				24
		1				l−					3							2							2			3				3
EJ θ(l) =−	m(l−0)		+		VA(			0)			−	q(l−0)			=−	2,5ql			l		+		2ql l				−		ql		=−5ql .
x		1					2				6							1							2			6				3
Окончательно из полученных выражений находим:
						y	= − 23ql4 ;								θ	c		= −	5ql3					.
						c			24EJx										3EJx

176

Прогибы получились отрицательные, следовательно, они направлены вниз (рис. 5.36). Углы поворота имеют знак «минус», т.е. поворот сечений В и С осуществляется по ходу часовой стрелки.

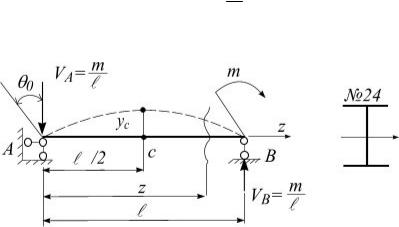
Пример 2. Для двухопорной балки (рис. 5.37) определить прогиб сечения в середине пролета и угол поворота сечения А.

Дано: m = 20 кН·м; ℓ = 6 м; Е = 2×105 МПа; Jx = 3460 см4.

Решение:

Определяем опорные реакции: VA =VB = ml .

Рис. 5.37

Помещаем начало координат на левой шарнирной опоре А. Очевидно, что прогиб на опоре равен нулю, а угол поворота нет.

Начальные параметры: y0 = 0 ,θ0 ≠ 0 .

Балка имеет один участок. Записываем универсальное уравнение прогибов (5.59), учитывая силы левее сечения z.

EJ	x	y(z) = EJ	θ	z −	VA(z −0)3	.	(а)
			x o	3

Дифференцируя его, получаем уравнение углов поворота:

EJ xθ(z) = EJ xθ0 −	V	A	(z −0)	2	.	(б)
			2

По уравнению (а) найдем начальный параметр θ0 из граничного условия на опоре В: при z = l, y = 0.

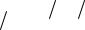
177

EJ

x

y

B

= EJ

θ

l−

VA(l−0)3

.

Откуда:

x o

6

EJ xθ0

=

VA (l−0)3

= m l,

(в)

6 l

6

θ0

=

m l

.

(г)

6EJ x

Подставляя в уравнение (а) выражение (в) и z =l/2, находим прогиб в середине пролета:

			EJx yc			= m l1 2 − m l(1 2 − 0)3			= m l2	,
						6	6		16
y	=		m l2	=		20 103 62		=6,5	10−3 м=0,65 см.
					16 2 1011 3460 10−8
c		16EJx

Прогиб yC направлен вверх. Угол поворота сечения А, совпадающего с началом координат, определим из выражения (г):

θA = θ0 =	m l	=	20 103 6		= 0,0029рад = 0,165o .
			6 2 1011 3460	10−8
	6EJ x

Поворот сечения А происходит против часовой стрелки.

Расчет балок на жесткость

В целях обеспечения нормальной эксплуатации строительных конструкций расчет изгибаемых элементов проводят не только по первой группе предельных состояний, но и по второй - на жесткость.

Во избежание появления чрезмерных перемещений наибольший прогиб ymax = f не должен превышать предельно допустимого, устанавливаемого

строительными нормами, т.е. должно выполняться условие жесткости:

f ≤ [f ] ,

(5.65)

178

где [ f ] = (200l ÷ 750l ) – допускаемый прогиб, указанный в долях пролета бал-

ки (задается СНиПом).

Если жесткость недостаточна, то необходимо подобрать другое сечение из условия (5.65).

Расчет на жесткость производят по нормативной нагрузке, т.е. без учета возможной перегрузки.

Тема 5.2 Общий вид эпюр внутренних усилий при изгибе

Изгибающая нагрузка в общем виде, формулы для вычисления опорных реакций

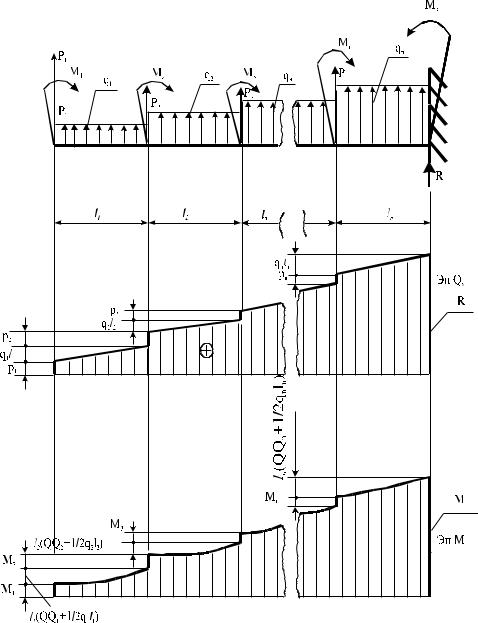
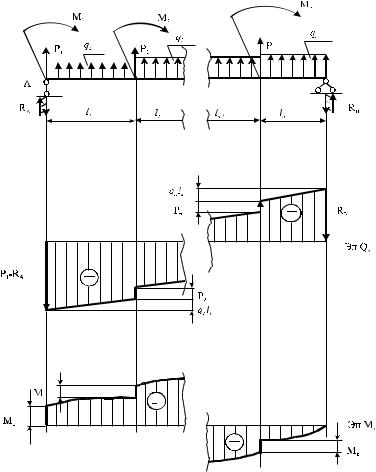
Изгиб балки происходит от нагрузки, перпендикулярной её продольной оси. Изобразим унифицированную схему консольной балки (рис. 5.38) и балки на двух опорах (рис. 5.39). Нагрузку представим в виде сосредоточенных сил Рi и моментов Мi, приложенных в начале каждого участка, а также распределенной нагрузкой по всей длине каждого участке интенсивности qi. За положительное принято направление нагрузки, вызывающее положительные изгибающие моменты. Балка может иметь n грузовых участков.

В случае двухопорных балок вначале расчёта нужно найти опорные реакции RА и RВ. Из уравнений равновесия ∑ мом А = 0 и ∑ пр y= 0, которые принимают вид:

P1(l1 + l2 +...+ ln )+P2(l2+l3+...+ln)+...+Pnln+ +q1l1(l1/2+l2 +...+ln)+q2l2(l2/2+l3+...+ln)+...+qnln2/2+

+M1+M2+...+Mn+RА(l1+l2+...+ln)=0, P1+P2+...+Pn+q1l1+q2l2+...+qnln+RА+RВ=0,

179

Рис. 5.38 Общий вид консольной балки

180

Рис. 5.39 Общий вид двухопорной балки

Следует

1

i=n

i=n

i=n

i=n

2

i=n

RA = −

∑M i + ∑ Pi + qi li ∑li

− ∑ qi li

/ 2

∑li ,

i=n

∑li

i=1

i=1

i

i=1

i

i=1

i=n

RB = −∑(Pi + qi li )− RA

i=1

Если величины RА и RВ получаем положительными, то они направлены вверх.

Формулы для вычисления внутренних усилий (поперечных сил и изгибающих моментов), общий вид их эпюр и закономерности

В расчётах на прочность необходимы эпюры поперечных сил Qy и изгибающих моментов Мx. Для компактного представления методики вычисления значений Qy и Мx используем i-й участок, который изобразим как отдельную консольную балку (рис.5.40), нагруженную на свободном краю сосредоточенной силой QQi и моментом MМi. По всей длине li покажем распределён-