u-lectures сопромат

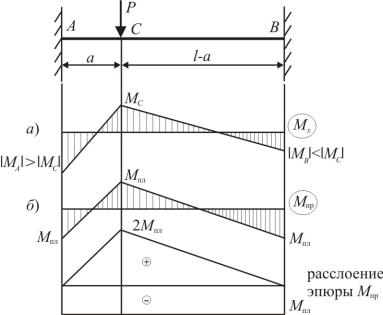
191

Рис. 5.49

Пусть наибольший по модулю изгибающий момент возникает в заделке A – M A . При увеличении нагрузки P этот момент достигнет значения

Mпр = σтWпл и в сечении A возникнет пластический шарнир. Однако несущая

способность балки еще не исчерпана. При дальнейшем увеличении нагрузки P пластический шарнир возникнет в сечении C и далее в сечении B. Наличие трех шарниров приведет к тому, что балка потеряет статическую неопределимость и превратится в механизм (геометрически изменяемую систему). Это и будет предельным состоянием, следовательно, в статически неопределимых балках необходимо возникновение k шарниров: k = c +1, где c – степень статической неопределимости. На эпюре моментов все «пики» равны значе-

нию Mпл (рис. 5.49, б).

Найдем приведенную нагрузку Pпр . Чтобы получить простую двух опорную балку, разложим эпюру Mпр на две составляющие: прямоугольник с высотой

равной Mпл		и треугольник с высотой 2Mпл .
Тогда 2M	пл	=	Pпрa(l − a)	, и отсюда выразим	P	=		M пл 2l	.
			l		пр		a(l − a)
Условие прочности будет иметь вид P ≤ [P					]=	Pпр		.
				пр		[n]

Балка составного сечения из разных материалов: нейтральная линия и формула для напряжений

192

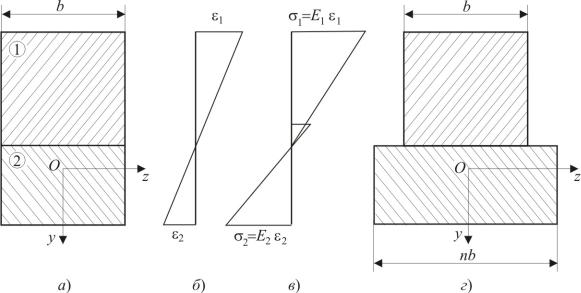
Балка, изготовленная из нескольких различных материалов, называется композитной балкой. Примерами являются балки, изготовленные из двух различных металлов, которые соединены друг с другом таким образом, чтобы работать как единое целое (биметаллические балки), железобетонные балки, а также трехслойные. Поскольку при чистом изгибе поперечные сечения балки остаются плоскими независимо от того, состоит ли балка из одного материала, замечаем, что в рассматриваемой балке деформации изменяются от верхней поверхности до нижней по линейному закону. На рис. 5.50 показано распределение этих деформаций. Для случая балки, которая изготовлена из двух различных материалов; поперечное сечение балки изображено на рис. 5.50, а. Сначала положение нейтральной оси поперечного сечения неизвестно, за исключением того случая, когда поперечное сечение обладает свойством двойной симметрии и когда нейтральная ось проходит на середине высоты балки.

а) поперечное сечение; б) распределение деформаций; в) эпюра напряжений; г) приведенное сечение.

Рис. 5.50. Балка, изготовленная из двух различных материалов

Нормальные напряжения, возникающие в поперечном сечении, можно получить умножением деформаций на модуль упругости соответствующего материала. В примере, приведенном на рис. 5.50, предполагается, что два материала, отмеченные цифрами 1 и 2, имеют соответственно модули упругости E1 и E2 . Тогда, считая, что E2 > E1 , получаем эпюру напряжений, построен-

ную на рис. 5.50, с. Нормальное напряжение σx на произвольном расстоянии y от нейтральной оси для материалов 1 и 2 соответственно задается следующими выражениями:

	193
σx1 = χE1 y , σx2 = χE2 y	(5.72)

Положение нейтральной оси можно найти, заметив, что суммарная осевая сила, действующая в поперечном сечении, равна нулю, откуда имеем

∫σx1dA + ∫σx 2 dA = 0 ,		(5.73)
1	2

где очевидно, что первый интеграл берется по площади поперечного сечения материала 1, а второй интеграл по площади поперечного сечения материала 2. Заменяя в этом равенстве σx1 и σx2 их выражениями (5.72), получаем

E1 ∫ydA + E2 ∫ydA = 0,		(5.74)
1	2

Это соотношение, которое в известном смысле представляется обобщением соотношения ∫ ydF = 0 , можно использовать для определения положения

нейтральной оси балки, изображенной на рис. 5.50. Однако для балок, изготовленных из трех и более материалов, потребуется ввести в соотношение (5.73) дополнительные члены аналогичного вида. Использовать это соотношение нетрудно, заметив, что интегралы представляют собой статические моменты частей площади поперечного сечения относительно нейтральной оси.

Соотношение между изгибающим моментом и напряжениями в балке:

M =∫σx ydA = ∫σx1 ydA + ∫σx 2 ydA =

	1	2	(5.75)
	= χE1 ∫y2 dA + χE2 ∫y2 dA = χ(E1 I1 + E2 I2 ),
	1	2

где I1 и I2 — соответственно моменты инерции площадей 1 и 2 относительно нейтральной оси. Отметим, что I = I1 + I2 , где I – осевой момент инерции

площади всего поперечного сечения.

Из формул (5.73) и (5.75) получаем следующие представления для напряжений в балке как функций от изгибающего момента M :

	σx1	=		MyE1		,		(5.76)
			E1I1		+ E2 I2
	σx2	=		MyE2			.	(5.77)
				E1I1	+ E2 I2

194

Первое выражение описывает распределение напряжений в материале 1, второе – в материале 2. Если E1 = E2 = E , то оба выражения упрощаются и сво-

дятся к виду σx = My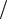I , как для балки из одного материала. Следующий

пример, иллюстрирует расчет балки, изготовленной из различных материалов.

Метод приведенного поперечного сечения

Метод приведенного поперечного сечения дает удобную процедуру исследования балки, изготовленной из различных материалов. Процедура заключается в преобразовании поперечного сечения балки, различные части которой изготовлены из различных материалов, в эквивалентное поперечное сечение балки, состоящей из одного материала. Затем последнее, называемое приведенным поперечным сечением, исследуется обычным способом, как и в случае балки из одного материала.

Для того чтобы быть эквивалентным поперечному сечению исходной балки, приведенное поперечное сечение должно иметь ту же нейтральную ось и ту же способность сопротивляться изгибающему моменту. Посмотрим, как находится приведенное поперечное сечение, и вернемся для этого к соотношению (5.74), которое определяет положение нейтральной оси. Разделив это соотношение на E1 и введя обозначение n = E2 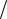E1 где n называется отношени-

ем модулей, получим

∫ydA + ∫yndA = 0 .		(5.78)
1	2

Отсюда следует, что положение нейтральной оси не изменится, если каждый элемент материала 2 площадью dA увеличится за счет коэффициента n при условии, что расстояние y для каждого такого элемента останется неизменным. Иначе говоря, поперечное сечение можно считать как бы состоящим из двух частей: из площади 1, которая остается прежней, и из площади 2, ширина которой умножается на n . Таким образом, получается новое поперечное сечение, полностью состоящее из одного материала, а именно из материала l. Приведенное поперечное сечение для балки (рис. 5.50, а) изображено на рис. 5.50, г. Часть сечения, занимаемая материалом 1, остается неизменной, а ширина части сечения, занимаемой материалом 2, увеличивается в n раз. (Заметим, что на рисунке принято n >1, но это не обязательно). Теперь приведенное поперечное сечение (рис. 1, г) уже можно считать целиком состоящим из материала 1. Нейтральная ось для приведенного поперечного сечения будет находиться там же, где и у исходной балки (рис. 5.50, а) — это следует из равенства (5.78). Кроме того, у приведенного сечения будет такая же, как и у исходного сечения, несущая способность по отношению к изгибающему мо-

195

менту (способность сопротивляться этому моменту). Указанное условие можно представить следующим образом. Для приведенного поперечного сечения справедливо соотношение σx = χE1 y , откуда получаем

M =∫σx ydA = ∫σx ydA + ∫σx ydA = χE1 ∫y2 dA + χE2 ∫y2 dA =

1

2

1

2

= χ(E1 I1 + E1nI2 )= χ(E1 I1 + E2 I2 ),

т. е. то же самое выражение, что и (5.75). Отсюда следует, что для исходной и для приведенной балок моменты одинаковы.

Напряжения в приведенном поперечном сечении можно найти из обычной формулы для напряжений, поскольку балка состоит только из одного материала. Такие напряжения определяются выражением

σx1 = M y , (5.79)

I

пр

где Iпр – момент инерции приведенного поперечного сечения относительно нейтральной оси ( Iпр = I1 + nI2 ). Выражения (5.79) и (5.76) совпадают; отсюда

заключаем, что напряжения в материале 1 исходной балки являются такими же, как и полученные для приведенного поперечного сечения. Однако для материала 2 в исходной балке подобное утверждение будет неверным. Наоборот, сравнение выражений (5.79) и (5.77) показывает, что для получения напряжений в исходной балке нужно напряжения в приведенной балке умножить на n. Таким образом, из вышеизложенного следует, что поскольку приведенное поперечное сечение состоит из материала 1, то напряжения в материале 1 будут «истинными», но напряжения в той части балки, которая состоит из материала 2, следует преобразовать с помощью отношения модулей. Метод приведенных поперечных сечений может быть легко распространен на случай, когда имеется более двух материалов. Точно так же можно привести исходную балку к балке из материала с произвольной величиной E , в этом случае все части поперечного сечения исходной балки должны быть соответственно приведены к этому фиктивному материалу. Разумеется, более простым и привычным является приведение к одному из исходных материалов, выбранному произвольно.

Контрольные вопросы к разделу 5

1.Какой вид деформации называется изгибом?

2.Дайте определения чистого и поперечного изгиба соответственно.

196

3.Поясните правило принятия знаков для изгибающего момента и поперечной силы.

4.Поясните суть основных дифференциальных соотношений теории изгиба.

5.Запишите формулу по определению нормальных напряжений, возникающих в поперечных сечениях при чистом и поперечном изгибе.

6.Запишите формулу Д.И. Журавского.

7.Поясните суть и предназначения метода начальных параметров.

8.Что такое главные центральные оси сечения и главные плоскости изгиба?

9.Какая геометрическая характеристика сечения является определяющим при оценке прочности балки по нормальным напряжениям при изгибе?

10.Где находятся опасные точки в поперечном сечении балки при чистом изгибе, поперечном изгибе?

11.Какая форма поперечного сечения балки при изгибе является рациональной и почему?

197

Модуль 2 Сложное сопротивление

Раздел 6. Основы теории напряженно-деформированного состояния Тема 6.1 Напряженное и деформированное состояние.

Полное, нормальное и касательное напряжения

Интенсивность нормальных сил в рассматриваемой точке сечения называется

нормальным напряжением σ, а интенсивность касательных сил – касательным напряжением τ.

Полное напряжение p определяется (см. раздел 1, тема 1.1):

p = σ2 + τ2.

(6.1)

Линейное напряженное состояние

Общие понятия о линейном, плоском и объемном напряженном состоянии см. раздел 1, тема 1.1.

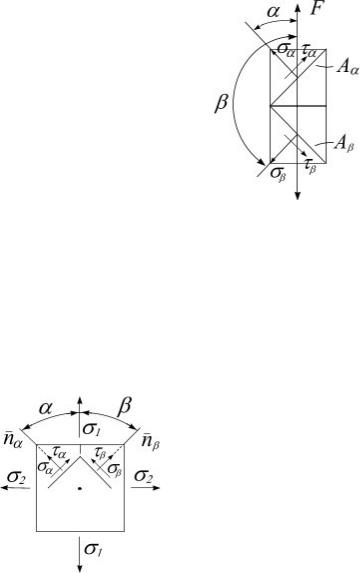
Линейное напряженное состояние реализуется при растяжении (сжатии) стержней (рис. 6.1). Напряжения в поперечном сечении

σ = σ	=	N	=	F	(6.2)
1		A		A

Напряжения на наклонных площадках Aα и Aβ в соответствии с формулами

2.9, 2.10:

σ	α	= σ cos2 α ; σ		β	= σ sin2 α		(6.3)
		1			1
		τα =	σ1 sin 2α	; τβ = −		σ1 sin 2α .	(6.4)
			2			2

По закону парности касательных напряжений τα =-τβ . Наибольшие касатель-

ные напряжения: τα =45o	= σ1	Главные напряжения: σ =σ;	σ	2	=σ	3	= 0
max	2	1

198

Рис. 6.1

Напряжения на произвольной площадке при плоском НС. Главные площадки и главные напряжения

При плоском напряженном состоянии на площадке α действуют нормальные и касательные напряжения (рис. 6.2).

Применяя принцип суперпозиции, на основании (6.3) и (6.4) имеем:

	σ	α	= σ cos2 α+ σ			2	sin2	α,
				1				(6.5)
	τα		=	σ1 −σ2	sin 2α.
				2

Рис. 6.2

Напряжения на площадке β = (900 −α), перпендикулярной площадке α , с учетом (6.5), будут определяться:

	σ	β	= σ sin2		α + σ	2	cos2	α,
				1				(6.6)
	τβ		=	σ1 − σ2	sin 2α.
				2

Из данных формул следует:

1. Касательные напряжения достигают максимальных значений при α± 450 и равны:

199

τmax =	σ1 −σ2 .	(6.7)
	2

2.Складывая выражения для нормальных напряжений (формулы 6.5 и 6.6), получим:

σα +σβ = σ1 + σ2 = const ,

т.е. сумма нормальных напряжений на взаимно перпендикулярных площадках постоянна и равна сумме главных напряжений.

3. Сопоставляя (6.5) и (6.6), получим τα = −τβ – закон парности касательных

напряжений.

При известных нормальных и касательных напряжениях по площадкам α и β могут быть установлены главные напряжения σ1 и σ2 , имеющие экстремальную (наибольшую и наименьшую) величину:

σ =	σα + σβ	±	1	(σ		− σ	)	2	+ 4τ	2	(6.8)
					α					α
1,2	2		2			β

	и направления главных напряжений
	tg2αo = −	τα	.	(6.9)
		σα − σβ

Приведенные формулы связывают главные напряжения и напряжения по наклонным площадкам.

В теории напряженного состояния различают две основные задачи:

Прямая – по известным главным площадкам и действующим на них главным напряжениям требуется определить нормальные и касательные напряжения на наклонных площадках под углом α ; Обратная – по известным нормальным и касательным напряжениям, дейст-

вующим на двух взаимно перпендикулярных площадках, найти главные напряжения и главные направления.

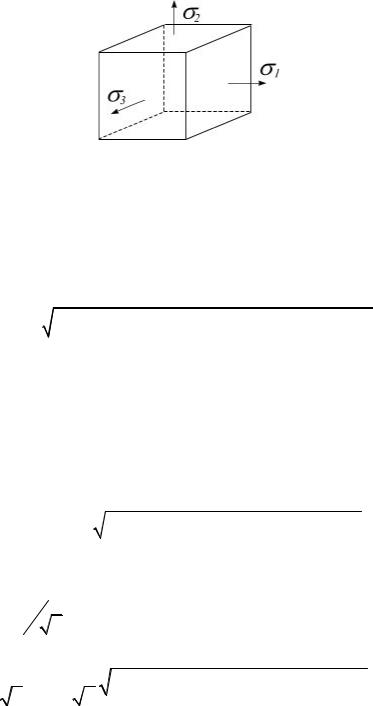
Объемное напряженное состояние

При действии σ1 , σ2 , σ3 в точке возникает объемное напряженное состояние

(рис. 6.3). Напряжения на площадках, параллельных одной из осей, определяются как для случая плоского напряженного состояния.

200

Рис. 6.3

Напряжения σα , τα на произвольной площадке определяются по формулам

σ		α	= σ cos2	α + σ	2	cos2 α	2	+ σ			3	cos2 α	;
			1	1								3
															(6.10)
τ	α		= σ2 cos2 α + σ2 cos2 α						2	+ σ2 cos2 α				3	−σ2 .
			1	1		2						3			α
Если нормаль к			произвольной			площадке						образует			одинаковые углы

α1 =α2 =α3 =α с направлениями σ1 , σ2 , σ3 , то площадка называется октаэдрической. Для такой площадки cos2 α =13, тогда:

α

α

= σ

окт

= σ1 + σ2 + σ3

= σ

cp

3

(6.11)

= 1

τ

α

= τ

окт

(σ −σ

)2

+ (σ

2

−σ

)2 + (σ −σ

)2 ,

3

1 2

3

1 3

где σокт , τокт – октаэдрические напряжения.

Величина, равная				3		2	τ		окт	, называется интенсивностью напряжений.
σ	i	=	3	τ		=			1		(σ −σ		)2	+ (σ		−σ	)2 + (σ −σ	)2 .	(6.12)
			2						2
					окт						1	2			2	3	1 3

Обобщенный закон Гука для изотропного материала

В общем случае при объемном состоянии действие напряжений σ1 , σ2 , σ3

вызывает деформации в направлении этих напряжений (рис. 6.3). Данные деформации можно определить на основе принципа независимости действия сил как сумму деформаций по каждому из направлений.

Продольная деформация в направлении σ1 от действия σ1 по закону Гука будет: