u-lectures сопромат

151

Очевидно, что	E	≠ 0 , следовательно, ∫ ydA = 0 , т.е. S x =0
	ρ	A

Интеграл представляет собой статический момент относительно нейтральной оси и равен нулю. Следовательно, нейтральная ось проходит через центр тяжести сечения.

E	∫ydA = 0 или	∫ yxdA = 0, т.е. J xy = 0 .
ρ	A	A

Центробежный момент равен нулю, значит, оси x, y – главные центральные оси. Так как силовая линия совпадает с осью y, а нейтральная ось с другой главной осью x, следовательно, силовая линия и нейтральная ось взаимно перпендикулярны.

Подставляя (5.19) в (5.16), найдем нормальные напряжения в сечение:

M = ∫ Ey ydA или M = E ∫ y2dA,

x A ρ x ρ A

где ∫ y2dA = Jx . Находим кривизну нейтрального слоя:

A

1	=	M x	.	(5.20)
ρ		EJx

Формулу (5.20) называют законом Гука при изгибе, а произведение EJx – жесткостью сечения при изгибе.

Подставляя	1	=	M x	(5.20) в σ = Ey	1		(5.19), находим
	ρ		EJx		ρ
				σ =			M x	y	(5.21)
							Jx

где у – расстояние от исследуемой точки до нейтральной оси.

Получена искомая формула, которая позволяет вычислять нормальные напряжения в любой точке поперечного сечения балки, при этом Мx и My удобнее брать по абсолютному значению, а знак σ устанавливать из характера деформирования балки.

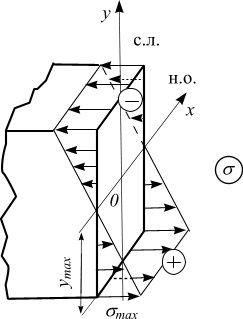
Пространственная эпюра σ изображена на рис. 5.19.

152

Рис. 5.19

Из анализа формулы (5.21) следует:

Напряжения σ изменяются по высоте сечения линейно;

По ширине сечения σ распределены равномерно (не зависят от координаты x);

Напряжения σ= 0 при y = 0, т.е. на нейтральной оси;

Напряжения максимальны там, где ymax , т.е. в точках наиболее удаленных от нейтральной оси; будем называть эти точки опасными.

		σmax	=	M x ymax ,		(5.22)
				Jx	M x ,
		или	σmax =			(5.23)
	Jx				Wx
где Wx =		,				(5.24)
	ymax

здесь Wx – осевой момент сопротивления сечения, характеризует сопротив-

ляемость балки изгибу, измеряется в см3, зависит от формы и размеров сечения.

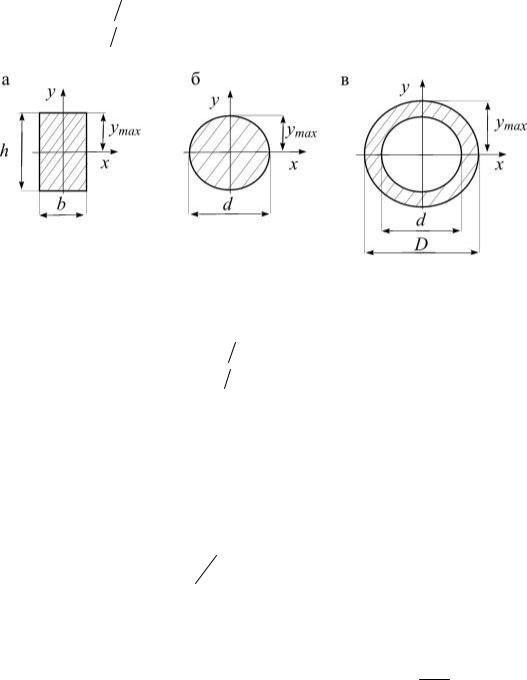
Определим осевые моменты сопротивления простых фигур по формуле

(5.24):

153

прямоугольник (рис. 5.20, а)

Wx	= bh3 12	= bh2	;	Wx	= bh2	, аналогично	Wy	= hb2 .	(5.25)
	h 2	6			6			6

Рис. 5.20

Круг (рис. 5.20, б)

Wy

=Wx

= πd 4

64

= πd 3

≈ 0,1d 3 .

(5.26)

d 2

32

Кольцо (рис. 5.20, в)

Jx =

πD4 −

πd 4

=

πD4 (1−α4 ),

где

α =

d

;

64

D

64

64

Wx =

Jx

=

πD4 (1−α4 ) =

πD3 (1−α4 ).

(5.27)

ymax

64 D

2

32

Обращаем внимание на то, что момент сопротивления подобного сечения нельзя считать как разность W =W1 −W2 , поскольку это противоречит самому

понятию о моменте сопротивления Wx как об отношении Jx .

ymax

Для прокатных профилей значения Wx и Wy приведены в таблицах сортамента.

Расчеты на прочность при чистом изгибе. Рациональные сечения балок

154

Балки из материалов, одинаково сопротивляющихся растяжению и сжатию (сталь), проектируются симметричными относительно оси x.

Условие прочности для них имеет вид:

по допускаемым напряжениям			по предельным состояниям
σmax =	M	max ≤ [σ]		σрасч.	=	M	расч.	≤ R γc	, (5.28)
						Wx
	Wx

где M расч. – наибольший по абсолютному значению изгибающий момент от

расчетных нагрузок;

R – расчетное сопротивление материала балки растяжению (сжатию) при изгибе; [σ] – допускаемое напряжение.

Условие (5.28) позволяет производить три вида расчета: Проверочный (непосредственно по указанному неравенству);

Проектный (подбор сечения)

Wx	= [σ]	и	Wx	= R γс .
	M расч.				M расч.

Определение несущей способности (допускаемого изгибающего момента)

M x max ≤Wx [σ] и Мрасч ≤Wx R γc .

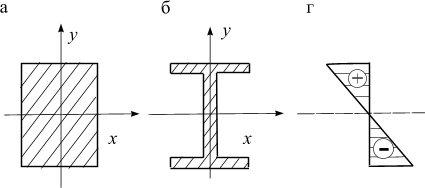
Характер распределения σ для симметричных сечений представлен на рис. 5.21, в.

Эпюра σ

Рис. 5.21

Из эпюры σ видно, что материал, расположенный у нейтральной оси, нагружен очень мало. В целях экономии и снижения веса балок следует выбирать

155

такие формы сечения, чтобы большая часть материала была удалена от нейтральной оси (рациональные формы). Наилучшим является двутавровое сечение (рис. 5.21, б).

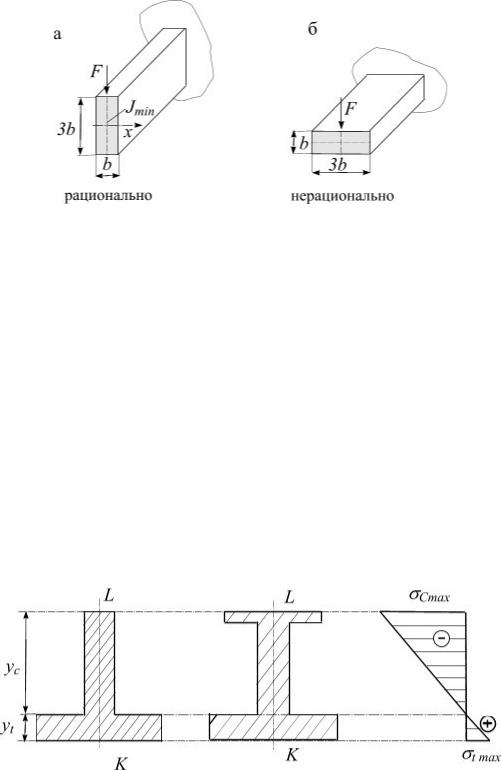
Менее выгодно прямоугольное сечение (рис. 5.21, а), особенно вытянутое вдоль нейтральной оси (рис. 5.22, б). Еще менее выгодно круговое сечение.

Рис. 5.22

Полое сечение всегда выгоднее сплошного, равноценного по площади. Наиболее экономичными являются сечения, для которых с наименьшей затратой материала получается наибольшая величина момента сопротивления.

Расход материала пропорционален площади сечения А, поэтому отношение W/А можно принять за критерий, оценивающий качество профиля. Рациональное расположение сечения имеет место, если силовая плоскость совпадает с плоскостью наибольшей жесткости (след ее совпадает с осью

Jmin ).

Для бруса (рис. 5.22, а) допускаемая нагрузка в три раза больше, чем для аналогичного бруса (рис. 5.22, б).

Для балок из хрупких материалов, различно сопротивляющихся растяжению и сжатию, следует применять сечения несимметричные относительно нейтральной оси (тавровое, несимметричное двутавровое, П–образное). При этом целесообразно располагать сечение так, чтобы большая его часть сечения находилась в растянутой зоне (рис. 5.23).

Рис. 5.23

156

При этом приходится отдельно проверять наибольшие напряжения в растянутой и сжатой зоне. Условие прочности (5.28) распадается на два:

σ

=

M x max

y

≤ [σ

]

σ

=

M расч.

y

р

≤ R γ

c

p max

k

p

Jx

ррасч.

J x

р

и

(5.29)

M x max

M расч.

σc max

=

yL

≤ [σc ]

σ

=

y ≤ R γ

Jx

срасч.

J x

c

c

c

где

yt

и yc – расстояния от нейтральной оси до наиболее удаленных точек

растянутой и сжатой зон;

R

и Rc

– расчетные сопротивления материала на

растяжение и сжатие; [σp ]ир[σc ] – допускаемые напряжения на растяжение и

сжатие.

Потенциальная энергия деформации при чистом изгибе

Работа статически приложенной силы в пределах упругих деформаций численно равна потенциальной энергии деформации.

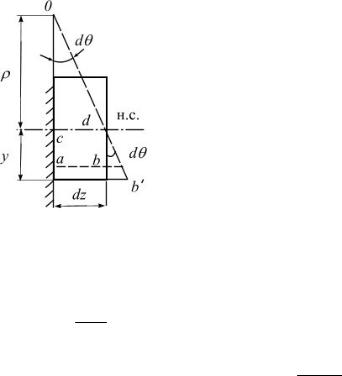
Работа изгибающего момента Мx при деформировании элемента dz (рис. 5.24) вычисляется как половина произведения момента на соответствующий угол поворота dθ .

dW = dU =	1 M x dθ.	(5.30)
	2

на нейтральной оси элемента dz = ρ dθ, отсюда:

dθ = ρ1 dz

По формуле (5.20)

Рис.5.24

1	=	M x	,
ρ		EJx

тогда dθ = M x dz . Подставляя это выражение в (5.30), имеем:

EJx

= M 2 dz dU x .

2EJ x

Суммируя значения dU по всей длине балки, получим формулу потенциальной энергии при чистом изгибе:

157

U = ∑∫	M 2 dz
	2EJx x .	(5.31)

При вычислении U следует учитывать, что закон изменения Мx для отдельных участков различен.

Поперечный изгиб балки Отличие поперечного изгиба от чистого

При поперечном изгибе:

Впоперечном сечении балки одновременно с изгибающим моментом возника-

ет поперечная сила (рис. 5.25, а, б).

Впоперечном сечении наряду с нормальными напряжениями возникают ка-

сательные напряжения τ (рис. 5.25, в)

Qy = ∫τyz dA .	(5.32)
A

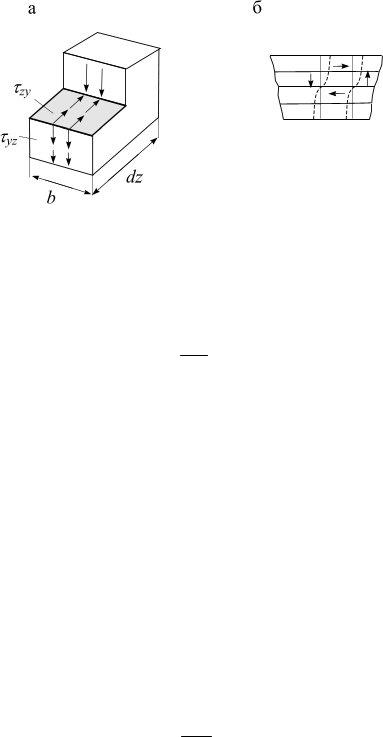
В продольных сечениях (рис. 5.26, а) на основании закона парности появляются касательные напряжения τyz , которые вызывают сдвиги отдельных воло-

кон.

Вследствие сдвигов волокон плоские сечения до деформации искривляются (рис. 5.26, б), принимая форму вытянутой буквы S, особенно в средней части балки, т.е. нарушается гипотеза плоских сечений.

Рис. 5.25

158

Рис.5.26

Так как сдвиг волокон не изменяет их длины, то найденный при чистом изгибе закон распределения σ остается в силе, и при поперечном изгибе применяют ту же формулу (5.21) для вычисления нормальных напряжений.

σ = M x y .

Jx

Касательные напряжения при изгибе. Формула Журавского

Статически неопределимая задача по определению напряжений может стать определимой, если ввести гипотезы (предположения) о характере распределения касательных напряжений в поперечном сечении балки:

касательные напряжения τ всюду параллельны Q;

касательные напряжения τ равномерно распределены по ширине сечения (на уровне y).

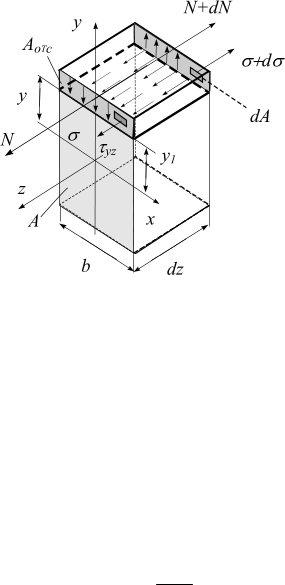
Отсечем верхнюю часть элемента балки dz, проведя горизонтальную плоскость на расстоянии y от нейтрального слоя (рис. 5.25, а). С правой стороны в каждой площадке dA напряжение больше на dσ (рис. 5.26), т.к. изгибающий момент справа больше, чем слева, на величину dM x (рис. 5.25, б), тогда:

dσ = M x y1 . J x

159

Рис. 5.26

Растягивающая сила N, действующая на отсеченную часть с правой стороны, больше, чем с левой, на величину

dN = ∫	dσdA = ∫	dM x	y1dA =	dM x		∫y1dA,	(5.33)
		J x
Aотс.	Aотс.			J x		Aотс.

где ∫y1dA = Sxотс. – статический момент отсеченной части относительно ней-

Aотс.
тральной оси x .
Поэтому
dN = dM x Sxотс. .	(5.34)
J x

Для того чтобы отсеченная часть элемента dz находилась в равновесии, в продольном сечении должны быть приложены касательные напряжения τyz ,

которые создают касательную силу dT. По условию равновесия ∑Z = 0 она должна быть равна силе dN:

dT = dN .

(5.35)

Сдвигающая сила dT определяется по формуле

dT = τzy by dz ,

(5.36)

где by – ширина сечения в той точке, где определяется касательное напряжение. По закону парности τyz = τzy = τ.

160

С учетом (5.34) и (5.36) выражение (5.35) перепишется:

			τzyby dz =		dM x	Sxотс. ,
или					J x
τ =	dM x		Sxотс.	.			(5.37)
	dz		by J x

Поскольку dMdzx = Qy , окончательно имеем:

τ =	Qy Sxотс.	(5.38)
	by J x

Формулу (5.38) называют формулой Журавского, который впервые установил наличие касательных напряжений при изгибе и показал, что в некоторых случаях разрушение балок происходит не от разрыва волокон, а от нарушения сопротивления сдвигу.

Примечание. Принципиально безразлично, брать ли Sxотс. заштрихованной

части или всей остальной части сечения, т.к. по абсолютному значению они равны: их сумма дает статический момент всего сечения относительно оси x, который равен нулю.

Анализ формулы Журавского

Из формулы (5.38) видно, что распределение касательных напряжений по высоте сечения зависит от его формы, т.е. величины Sxотс. by .

Прямоугольное сечение

Через произвольную точку К (рис. 5.27, а), отстоящую от нейтральной оси на расстоянии y, проведем сечение, параллельное оси x. Ширина сечения by = b ,

момент инерции Jx = bh3 12.