u-lectures сопромат

81

угольник, двутавр, круг и т.д.) центром тяжести является точка пересечения этих осей. Если сечение имеет одну ось симметрии (швеллер, равнополочный уголок и т.д.), то для определения положения центра тяжести необходимо найти только одну координату – вдоль оси симметрии.

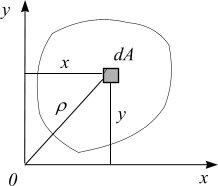
Пример. Определить положение центра тяжести сечения, изображенного на рис. 3.3.

Решение

Сечение симметрично относительно оси у. Следовательно, центр тяжести С лежит на этой оси, т.е. координата хс=0, и остается найти координату ус. Все размеры показаны на рисунке указаны в сантиметрах.

Рис.3.3

Разбиваем фигуру на два прямоугольника: первый – с центром тяжести С1 и площадью

A1 = 6 2 =12 см2.

Второй – с центром тяжести С2 и площадью

A2 = 8 3 = 24 см2.

За вспомогательную ось принимаем центральную ось первого прямоугольника х1. Тогда статический момент его площади S1x1 = 0 . Статический момент

площади второго прямоугольника согласно формулам (3.3) составляет

S	2 x	= A y	c2	= 24(8/ 2 + 2 / 2) = 24 5 =120 см3.
		2
	1

Координата центра тяжести всего сечения согласно формулам (3.5):

82

y = ∑Sx1		=	S1x1	+ S2 x2	= 0 +120	= 3,3 см.
c	∑A		A1	+ A2	12 + 24

Положительное значение свидетельствует о том, что центр тяжести С лежит выше оси х1.

Примечание. Заметим, что точка С лежит на прямой С1С2 соединяющей центры тяжести прямоугольников, и разбивает ее на отрезки обратно пропорциональные площадям:

	A2	=	CC1		или	24	=	3,33	= 2.
	A					12		1,67
			CC	2
	1

Моменты инерции сечений

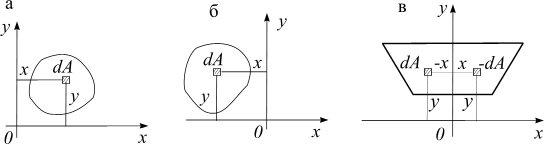
Осевым моментом инерции сечения относительно данной оси называется взятая по всей его площади A сумма произведений элементарных площадок dA на квадраты их расстояний до этой оси.

Осевые моменты инерции относительно осей х и у равны (рис. 3.4).

Рис.3.4

J x = ∫y2dA,	J y = ∫x2dA.	(3.6)
A	A

Пусть ρ – расстояние элементарной площади до точки О (рис. 3.4).

Полярным моментом инерции сечения относительно некоторой точки (по-

люса) называется взятая по всей его площади A сумма произведений элементарных площадок dA на квадраты их расстояний ρ до этой точки. Следовательно

J p = ∫ρ2dA.	(3.7)
A

83

Как видно из рисунка 3.4: ρ 2= x2 + y2 , тогда

Jρ = ∫(x2 + y2 )dA = ∫x2dA + ∫y2dA = J у + Jх;

A	A	A
Следовательно,		(3.8)
	Jρ = Jx + J y .

Полярный момент инерции J ρ равен сумме осевых моментов инерции J x и J y , взятых относительно любой пары взаимно перпендикулярных осей x и y,

проходящих через полюс О.

Отметим, что осевые и полярные моменты инерции всегда положительны.

Центробежным моментом инерции сечения относительно осей координат x

и y называется взятая по всей его площади A сумма произведений элементарных площадок dA на их расстояния до этих осей:

J xy = ∫xydA .	(3.9)
A

Моменты инерции выражаются в см4, м4.

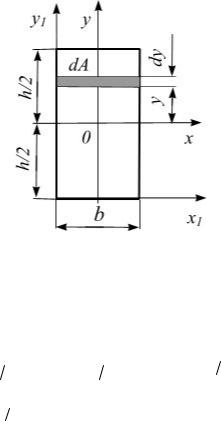
В зависимости от положения осей центробежный момент инерции может быть положительным, отрицательным или равным нулю. Так, например, центробежный момент сечения, показано на рис. 3.5 а, относительно осей х и у положителен, так как сечение расположено в первом квадрате и значения ко-

ординат х и у всех элементов положительны, а следовательно, и ∫xydA положительны.

Рис.3.5

Центробежный момент сечения (рис.3.5, б) расположенного во втором квадрате будет иметь отрицательное значение, так как координаты у всех элементов положительны, а координаты х – отрицательны.

Для фигуры симметричной, например, относительно оси у (рис.3.5, в), каждой

84

положительной величине xydA соответствует такая же отрицательная величина, по другую сторону от оси симметрии и их сумма по всей площади фигуры равна нулю. Таким образом, центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.

Оси, относительно которых центробежный момент равен нулю, называются главными осями инерции. Главные оси, проходящие через центр тяжести се-

чения, называют главными центральными осями.

Моменты инерции простых фигур

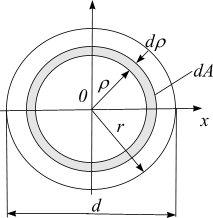
Вычислим моменты инерции прямоугольника относительно центральных осей x и y, параллельных его сторонам (рис. 3.6).

Рис.3.6

Выделим элементарную площадку в виде узкого прямоугольника dA = b dy . Подставляя значение dA в формулу (3.6) и интегрируя, получим

	h 2	h 2	y3			h 2		h3		bh3
J x = ∫ y2dA =	∫ y2bdy = 2b ∫y2dy = 2b						= 2b		=
A	−h 2	0	3			0	24		12

По аналогии можно вычислить J y и окончательно формулы для осевых мо-

ментов инерции относительно центральных осей имеют вид:

	J x =	bh3		J y =	hb3
			;			.	(3.10)
		12			12

Для осей x1 и y1, проходящих через основание, изменяя пределы интегрирова-

85

ния, получаем:

	h		h					y	3			h			h	3		bh	3
J x = ∫ y 2 dA = ∫ y 2bdy = b∫ y 2 dy = b														= b			=
							3
A	0		0									0		3			3
	J x =	bh3		;	J y	=		hb		3									(3.11)
			3						3
	1				1
Центробежный момент инерции J xy			= 0		, т. к. оси x и y являются осями сим-

метрии.

Вычислим полярный момент инерции круга относительно его центра (рис.

3.7). Выделим бесконечно тонкое кольцо, площадь которого равна

dA = 2πρ dρ.

y

Рис. 3.7

Подставляя значение dA в выражение (3.7) и интегрируя, получим

	r	πr	4		πd	4
Jρ = ∫ρ2 dA = 2π∫ρ3dρ =				=			.	(3.12)
A	O	2			32

На основании выражения Jρ = J x + J y и в силу симметрии получим осевые моменты инерции круга:

	J x = J y =	1	Jρ =	πr	4	πd 4	.	(3.13)
					=
		2		4		64

Полярный момент инерции кольцевого сечения (рис. 3.8) найдем как разность моментов инерции большого круга диаметром D и малого круга диаметром d:

Jρ =	πD4	−	πd 4	=	πD4	(1 − α4 ) .	(3.14)
	32		32		32

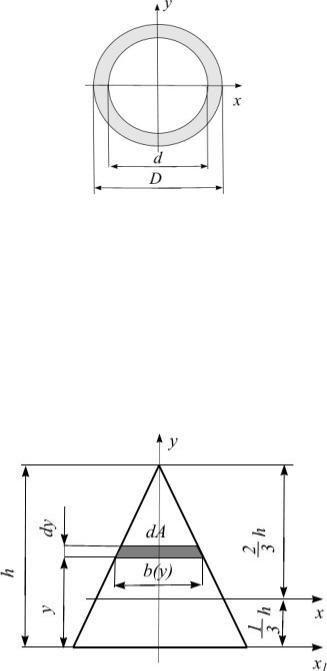
86

Рис. 3.8

Осевые моменты инерции кольца:

J x = J y =	1	Jρ =	πD4	(1 − α4 ) .	(3.15)
	2		64

Найдем момент инерции треугольника относительно оси x1, проходящей через его основание (рис. 3.9).

Рис. 3.9

Разбиваем площадь фигуры на элементарные полоски, параллельные данной оси. Ширина полоски, находящейся на расстоянии у от оси x1:

b(y)= b	(h − y)			y
	h	= b 1	−		.
				h

Тогда площадь полоски:

87

dA = b( y)dy = b(1 − hy) dy .

Подставляя dA в формулу (3.6) и интегрируя, получим

	Jx1 = ∫y2dA = ∫h b(1−					y	) y2dy = bh3 .
						h
	A	O					12
	Окончательно			bh3
		Jx1	=				.
					12
	Относительно центральной оси
		J xC	=		bh3		.
					36

(3.16)

(3.17)

Для прокатных профилей (двутавры, швеллеры, уголки и т.д.) моменты инерции и другие геометрические характеристики находят в сортаменте (таблицы прокатных профилей, поставляемых металлургическими заводами в соответствии с требованиями ГОСТов).

Моменты сопротивления

Такие геометрические характеристики, как осевые и полярные моменты сопротивления сечения, используются при расчетах элементов конструкций на прочность при изгибе и кручении соответственно.

Осевые моменты сопротивления:

Wx =	J	x	, Wу =	J у	(3.18)
				xmax
	ymax

Wx,Wy характеризуют сопротивляемость балки изгибу, измеряются в см3, зависят от формы и размеров сечения.

Моменты сопротивления простых фигур по формуле (3.18):

прямоугольник (рис. 3.10, а)

Wx =	bh3	12	=	bh2	;	Wx =	bh2	, аналогично	Wy	=	hb	2	.	(3.19)
	h	2		6			6				6

88

Рис.3.10

Круг (рис. 3.10, б)

= πd 4

πd 3

Wy =Wx

64 =

≈ 0,1d 3 .

(3.20)

d 2

32

Кольцо (рис. 3.10, в)

J x

= πD4

−

πd 4

=

πD 4

(1−α4 ),

где

α =

d

;

64

64

D

64

Wx =

J x

=

πD 4 (1−α4 )

=

πD3

(1−α

4

).

(3.21)

ymax

64

D

2

32

Обращаем внимание на то, что момент сопротивления подобного сечения нельзя считать как разность W =W1 −W2 , поскольку это противоречит само-

му понятию Wx как отношению	J x	.
	ymax

Для прокатных профилей значения Wx и Wy приведены в таблицах сортамен-

та.

Полярные моменты сопротивления

Геометрическая характеристика сечения, называемая полярным моментом сопротивления, см3 или м3определяется по формуле:

	W	=	Jρ					(3.22)
			ρ max
	ρ						Jρ
	Вычислим полярный момент сопротивления				W	=		для круга и кольца.
							ρ max
					ρ

По формулам (3.13) и (3.14) имеем:

89

Jρ =	πd 4	и	Jρ =	πd 4	(1 − α4 ) ,	(3.23)
	32			32

где α = Dd – отношение внутреннего диаметра к наружному (рис. 3.8).

Тогда моменты сопротивления для сплошного круглого сечения:

	Wρ =	Jρ		=	πd 3	,	(3.24)
		d	2		16

для кольцевого сечения:

	Wρ =	Jρ	=	πD3	(1−α4 ) .	(3.25)
		d 2		16

Определение геометрических характеристик сложных сечений, в том числе, моментов инерции, проводится с использованием формул «параллельного переноса», которые приведены в теме 3.2.

Тема 3.2 Главные моменты инерции

Графическое представление моментов инерции. Понятие о радиусе и эллипсе инерции

Предположим, что известны моменты инерции J x , J y и J xy относительно

центральных осей бруса заданного сечения (рис. 3.11, а). Требуется определить положение главных осей инерции и величину главных моментов инерции. Для определенности построения примем J x > J y и J xy > 0 .

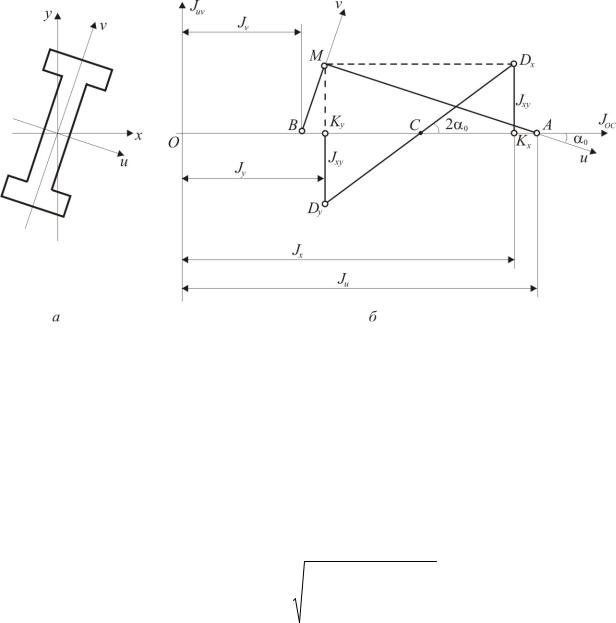
90

Рис. 3.11

В геометрической плоскости (рис. 3.11, б) строим точки Dx и Dy , соответствующие моментам инерции относительно осей x и y . Абсциссы этих точек являются осевыми моментами инерции: OK x = J x , OK y = J y ; ординаты – центробежные моменты инерции J xy , причем Kx Dx = J xy , K y Dy = −J xy . Так

как обе точки принадлежат одному диаметру, то соединив их, получим центр инерции C , из которого описываем окружность радиуса

		J	x	−	J	y		2
								2
СDx = СDy =								+ J xy ,
				2
Пересекающую ось абсцисс в точках		A и B .						Очевидно, что абсциссы этих

точек (OA и OB ) являются искомыми главными моментами инерции Ju и

Jv .

Для определения направления главных осей построим фокус круга инерции. Для этого из точек Dx и Dy проводим линии, соответственно параллельно

указанным осям, до пересечения с кругом в точке M . Соединив затем фокус с точками A и B круга, получим направление главных осей u и v (рис. 3.11,

б).

Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, назы-

ваемой радиусом инерции: