Траектории частиц и линии тока

Траекторией движущейся частицы называется путь одной и той же частицы, прослеженной во времени. Изучение траекторий частиц лежит в основе метода Лагранжа.

В пространстве, занятом движущейся жидкостью, выделим в некоторый момент точку 1, вектор скорости в которой . В тот же момент времени по направлению вектора на бесконечном расстоянии dℓ возьмем точку 2, в которой вектор скорости и т.д. При бесконечно большом количестве точек огибающая всех этих векторов даст в пределе некоторую пространственную кривую, называемую линией тока и показанную на рис.7.1.

Линия тока представляет собой такую линию, в каждой точке которой в данный момент времени t векторы скорости являются касательными к этой линии. В векторной форме это условие может быть записано как . Векторное произведение может быть записано в виде определителя

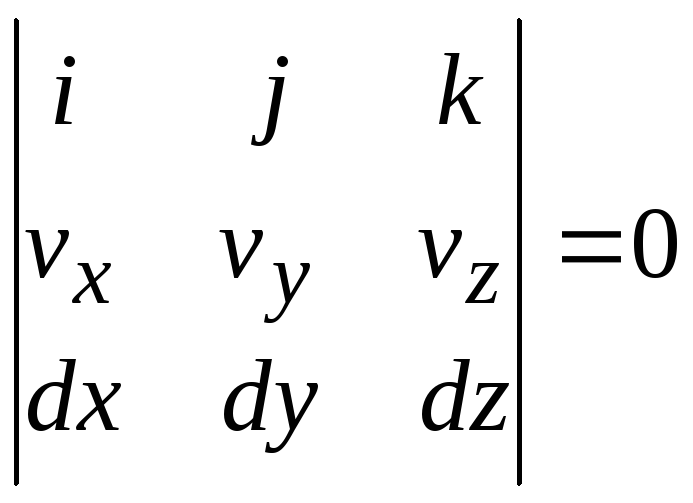. (7.10)

Отсюда для линии тока

или .

Тогда

.

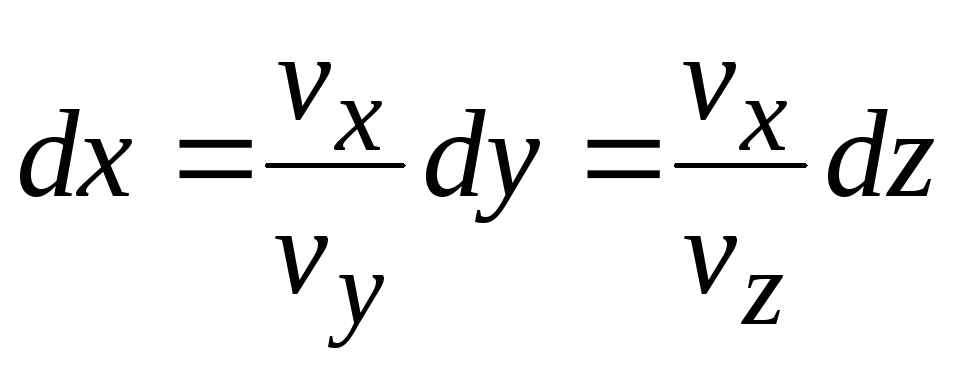Разделив это выражение на v_x, получаем дифференциальное уравнение линии тока

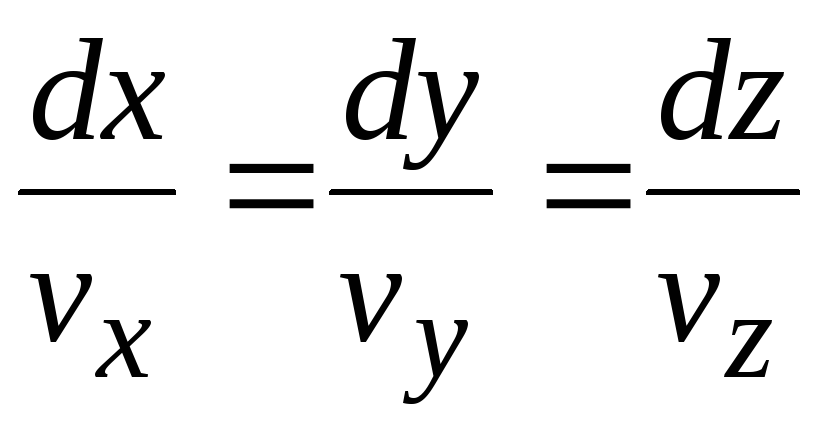. (7.11)

Движение отдельно выделенной частицы описывается в переменных Лагранжа. Для этой частицы в любой точке пространства и в любое время проекции скорости на координатные оси равны

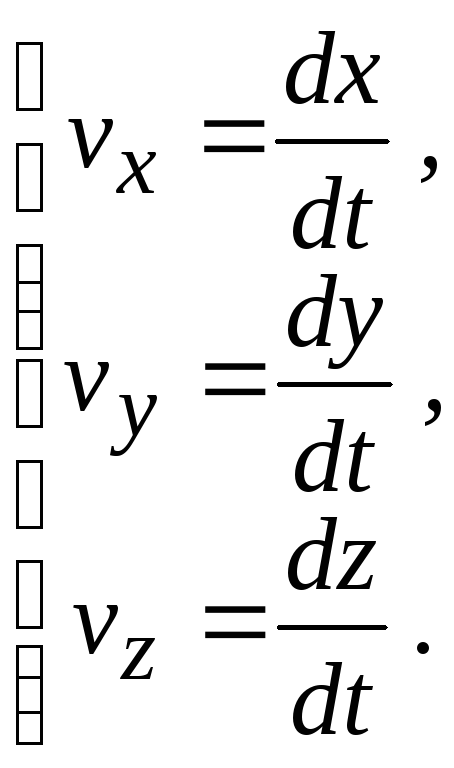(7.12)

Отсюда дифференциальное уравнение траектории

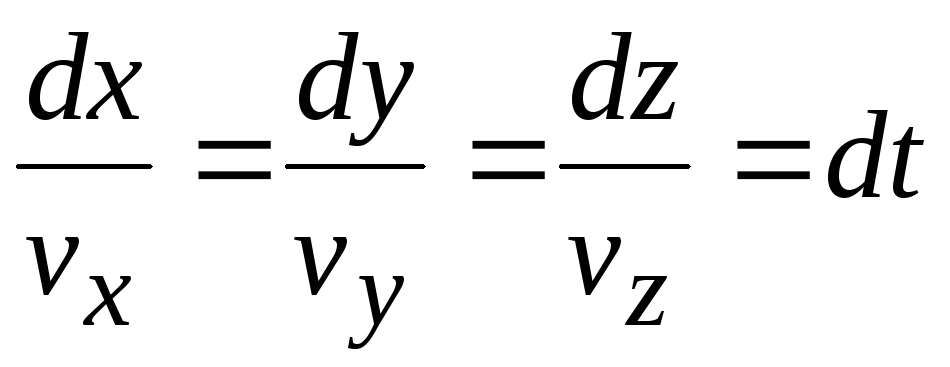. (7.13)

Из сопоставления (7.11) и (7.13) видно, что в общем случае, т.е. при неустановившемся движении линии тока и траектории не совпадают. Это объясняется тем, что касательные к линии тока дают направления скорости разных частиц жидкости в последовательных точках пространства в определенный момент времени, а касательные к траектории дают направление скорости определенных частиц в последовательные моменты времени. Поэтому линии тока совпадают с траекториями только при установившемся движении, когда поле скоростей не меняется во времени, т.е. скорости частицы не зависят от dt.

Линии тока можно сделать видимыми, если поверхность жидкости посыпать частицами такого вещества, которое может двигаться вместе с жидкостью. Можно ввести такие частицы также внутрь жидкости. При съемке с короткой выдержкой каждая введенная в жидкость частица оставляет в кадре короткую черточку. При достаточно большом числе частиц черточки тесно примыкают друг к другу и дают картину линий тока. Для получения траекторий необходимо уменьшить количество вводимых частиц и производить съемку с длительной выдержкой.

Если провести линии тока через все точки какого-нибудь небольшого замкнутого контура, то эти линии образуют на сколь угодно большом протяжении так называемую трубку тока (рис.7.2).

Такая трубка обладает той особенностью, что жидкость внутри нее в рассматриваемый момент времени течет, как в трубе с твердыми стенками. Жидкость, текущая внутри трубки тока, называется жидкой струйкой. При установившихся течениях трубки тока сохраняются неизменными все время. Мысленно разбивая все пространство, занятое жидкостью, на трубки тока, можно получить очень наглядное представление о течении жидкости.

Для облегчения изучения законов гидрогазодинамики действительное движение жидкостей заменяется условной схемой, в которой поток жидкости рассматривается как совокупность отдельных частиц, образующих элементарные струйки. Эту схему называют «струйчатой моделью движения жидкости». Элементарная струйка обладает следующими свойствами. При установившемся движении струйка не меняет своей формы и ориентации в пространстве: в этом случае ни одна частица жидкости не может проникнуть внутрь струйки или выйти из нее, т, е. обмена между струйками не происходит. Вследствие малой величины сечения струйки скорости и давление во всех точках сечения являются одинаковыми.

Совокупность элементарных струек, представляющих собой непрерывную массу частиц, движущихся в определенном направлении с различными скоростями, называется потоком жидкости.

При решении многих простых задач, например, при изучении движения жидкостей в трубах и каналах, допустимо рассматривать все пространство, занятое потоком жидкости, как одну единственную жидкую струйку.

Живым сечением потока называется его поперечное сечение s, перпендикулярное направлению движения. Площадь живого сечения потоков в трубах и рукавах рассчитывается по формуле

. (7.14)

Смоченным периметром χ называется линия, по которой живое сечение потока соприкасается с твердыми, ограничивающими его стенками.

В водопроводной трубе он равен

. (7.15)

Отношение площади живого сечения ω к смоченному периметру называется гидравлическим радиусом R

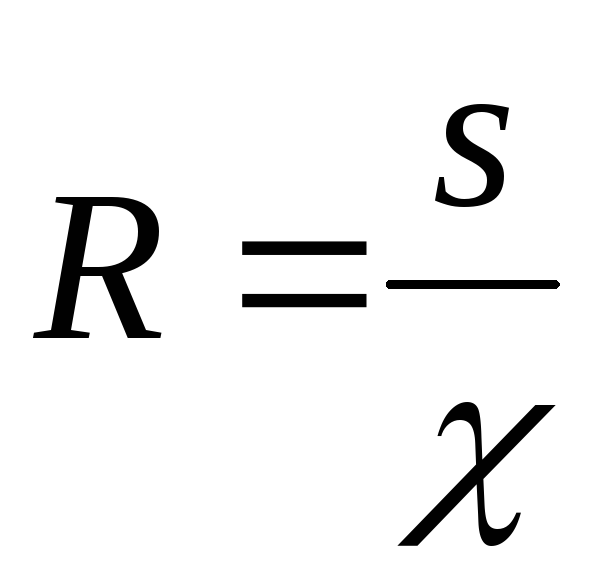. (7.16)

Необходимо отметить, что для круглых живых сечений гидравлический радиус R не равен геометрическому r. В этом случае

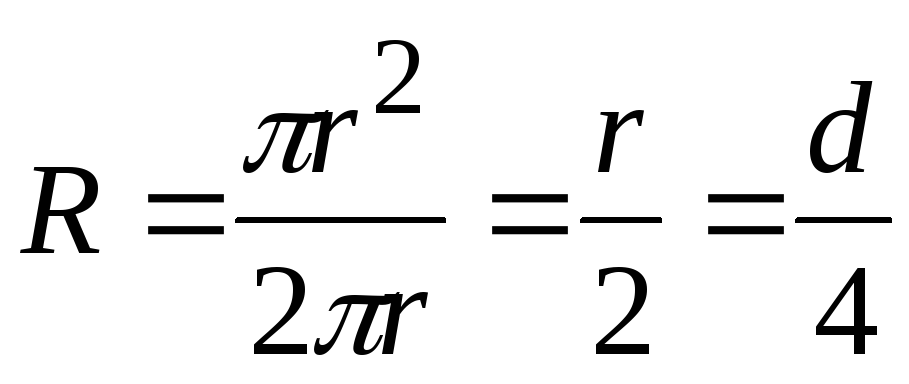. (7.17)

Объемным расходом жидкости Q через какую-либо поверхность называют объем жидкости, протекающим через живое сечение в единицу времени. Объемный расход элементарной струйки с живым сечением ds равен

. (7.18)

Полный расход равен сумме расходов элементарных струек, пересекающих это сечение

. (7.19)

Массовым расходом жидкости G называют массу жидкости, проходящую через живое сечение в единицу времени.

, (7.20)

. (7.21)

Довольно часто при решении практических задач пользуются средней скоростью потока , равной отношению объемного расхода к живому сечению

. (7.22)

Средняя скорость в сечении представляет такую абстрактную (воображаемую) одинаковую для всех точек сечения скорость, при которой через сечение проходил бы тот же расход, какой имеет место при действительных скоростях, различных для разных точек сечения.

Лекция 8. ДВИЖЕНИЕ ЭЛЕМЕНТАРНОГО ОБЪЕМА

ЖИДКОЙ ЧАСТИЦЫ

Первая теорема Гемгольца

Из механики твердого тела известно, что всякое движение твердого тела в бесконечно малый промежуток времени может быть разложено на поступательное движение со скоростью некоторой точки тела и вращательное движение вокруг мгновенной оси, проходящей через эту точку.

Движение жидкой частицы является более сложным, т.к. жидкая частица может изменять свой объем. Рассмотрим жидкую частицу в форме прямоугольного параллелепипеда с ребрами длиной dx, dy, dz. В общем случае частица может двигаться поступательно со скоростью , при этом вращаясь со скоростью и деформируясь со скоростью . Отсюда

. (8.1)

Рассмотрим декартову систему координат и примем, что она движется вместе с частицей поступательно со скоростью . В этой системе присутствует только вращательное и деформационное движение частицы. Для описания движения всей частицы достаточно описать движение ее ребер.

Деформация жидкой частицы может быть линейной вследствие изменения длины ребер, так и угловой из-за деформации углов параллелепипеда. Рассмотрим сначала угловую деформацию только для одной грани, расположенной в плоскости хОу.

Угловая деформация может возникнуть из-за разности скоростей, перпендикулярных ребрам. Допустим, что проекции скорости на координатные оси в точке А соответственно равны v_x,A, v_у,A, v_z,A. Считая движение частицы установившимся, определим проекции скорости в точке В:

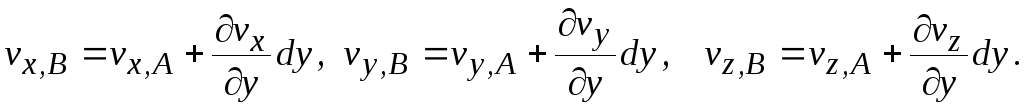
За время dt точка В сместится в точку В₁. Расстояние ВВ₁ будет равно

.

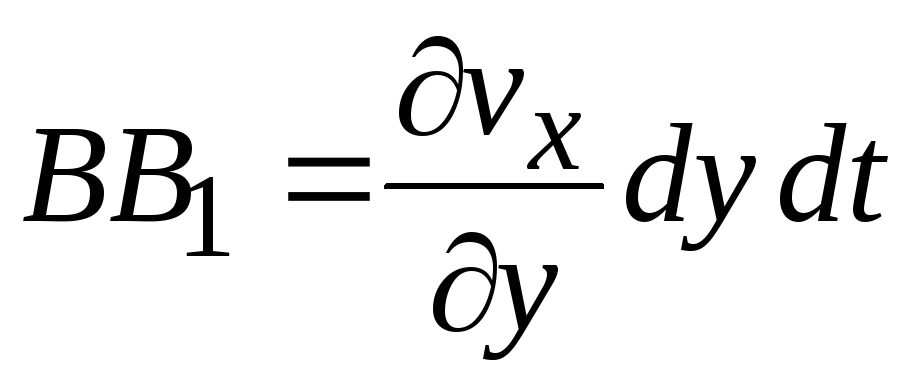Угловая деформация характеризуется изменением положения ребер, т.е. величиной d. Ввиду малости угла можно принять

.

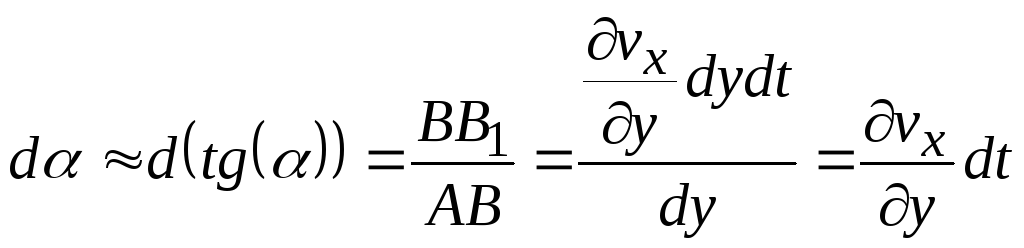Аналогичным образом определим проекции скорости в точке D:

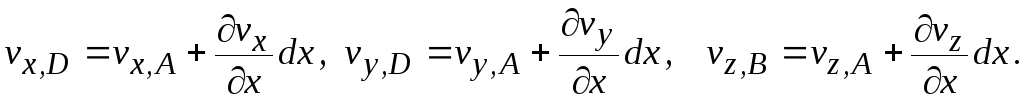
Величина угла

.

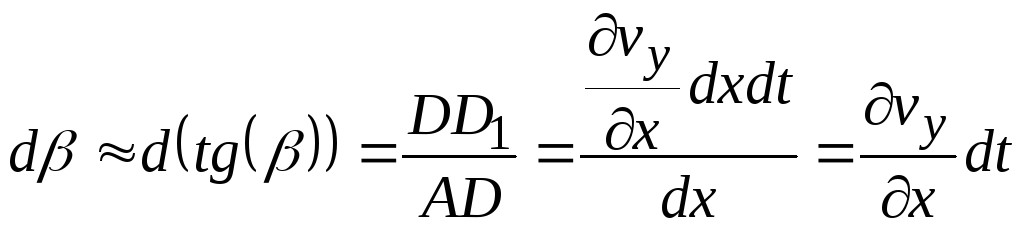Полное изменение прямого угла в точке А составит

.

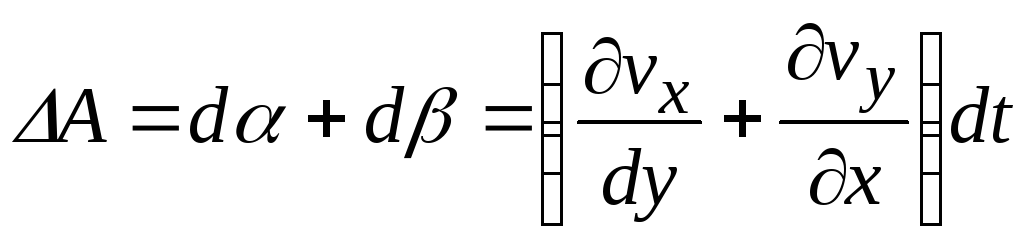Следует обратить внимание на существенное обстоятельство. Поворот ребер может быть вызван как деформацией параллелепипеда, так и поворотом его без деформации. Если бы ребра поворачивались только вследствие деформации без вращения параллелепипеда, то за время dt они повернулись бы на один и тот же угол d навстречу друг другу. Если бы ребра поворачивались только вследствие поворота параллелепипеда без его деформации, то они повернулись бы на один и тот же угол d в одну и ту же сторону.

Предположим, что вращение параллелепипеда происходит против часовой стрелки в положительном направлении, как показано на рис.8.2.

Из рисунка следует, что

,

.

Складывая и вычитая эти уравнения, получим

,

.

Таким образом, деформация характеризуется полусуммой углов, а вращение – полуразностью.

С учетом найденных выше значений углов d и d скорость деформации относительно оси z составит

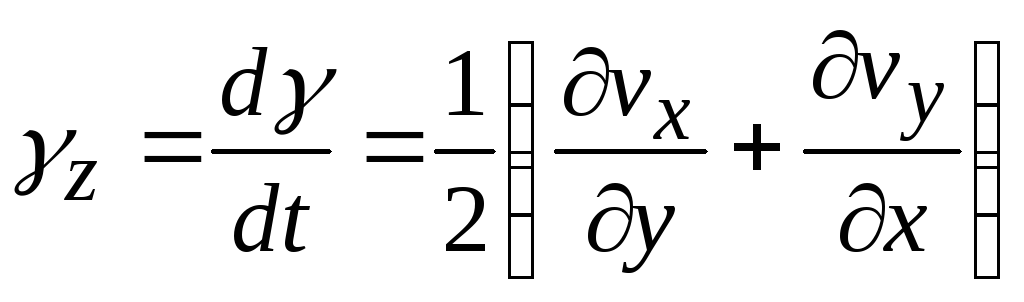. (8.2)

По аналогии с (5.2) имеем

, (8.3)

. (8.4)

Выражение 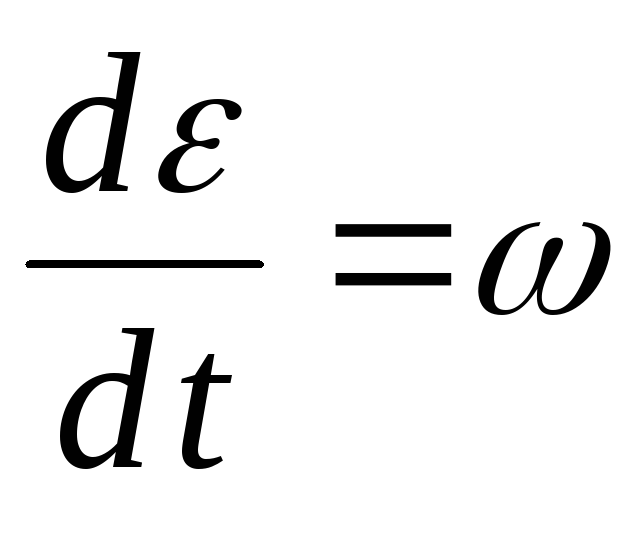есть угловая скорость вращения жидкой частицы. Проекции угловых скоростей на координатные оси

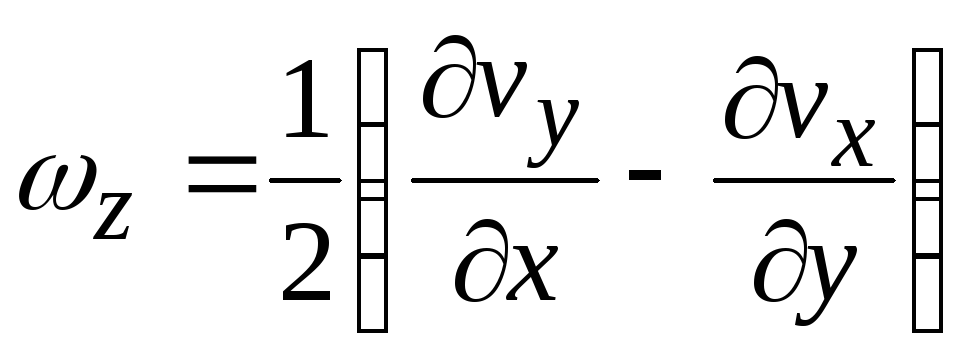, (8.5)

, (8.6)

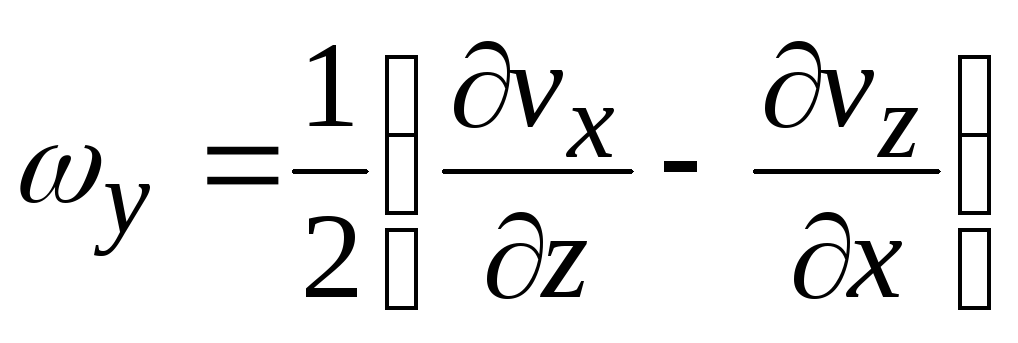. (8.7)

Для угловой скорости может быть представлено обобщенное уравнение в векторной форме:

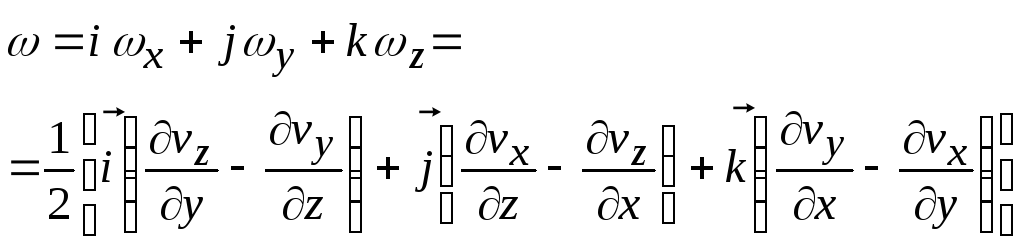. (8.8)

В теории векторного поля определены несколько операций над векторами и скалярными величинами, позволяющих более полно описать свойства полей. Для скалярной величины (x,y,z), описывающей распределение некоторого скалярного параметра в пространстве, например, плотности или температуры, определен вектор, называемый градиентом и указывающий направление наибольшего увеличения величины . Скорость увеличения  равна длине вектора. В декартовых координатах градиент от  представляется в виде

. (8.9)

Так как величина и направление градиента зависят от точки пространства, то градиент также создает свое поле в пространстве.

Для векторной характеристики поля , например, скорости жидкости в пространстве, определена скалярная величина , которая называется дивергенцией или расхождением и рассчитывается по формуле

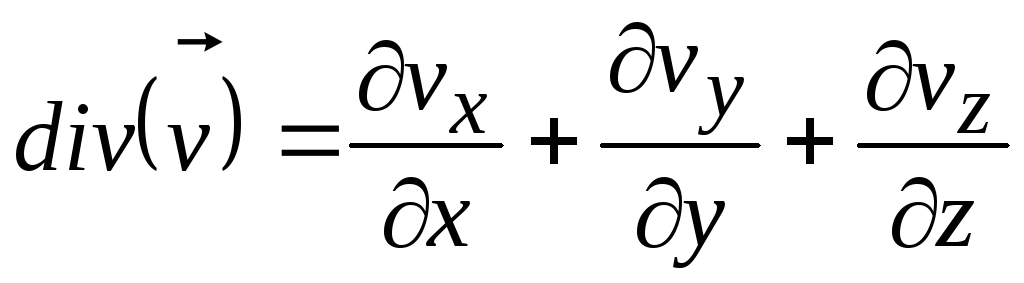. (8.10)

Дивергенция определяет наличие и мощность источников и стоков векторной величины в рассматриваемой точке пространства. При векторное поле называется соленоидальным или трубчатым, т.е не имеющим внутри окрестности точки источников и стоков величины .

Для также определена векторная величина , которая называется ротором или вихрем и рассчитывается по формуле

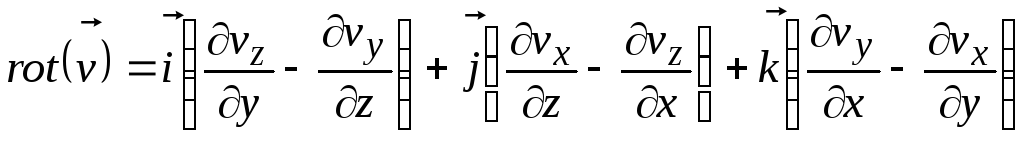. (8.11)

Выражение для ротора можно представить в виде определителя

.

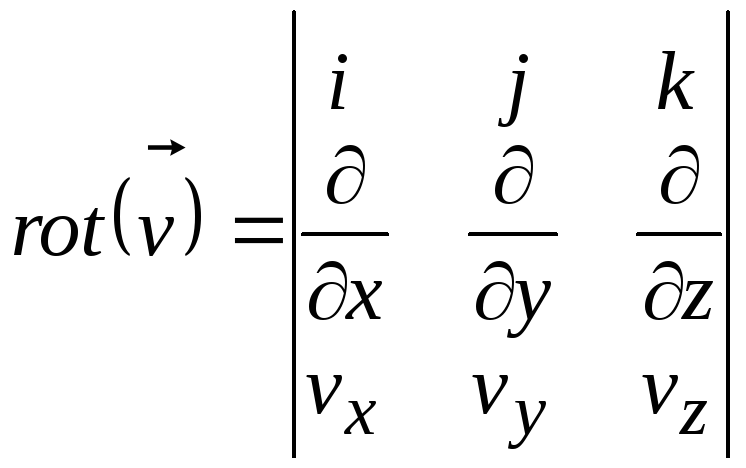Ротор определяет наличие и интенсивность вихрей величины в рассматриваемой точке пространства. При векторное поле называется безвихревым.

В соответствии с (8.11) можно записать

, (8.12)

т.е. угловая скорость вращения жидкой частицы равна половине ротора векторного поля линейной скорости частицы в рассматриваемой точке.

Следует обратить внимание на то, что угловая скорость частицы, определяемая выражением (5.8), является общей для всего объема частицы. Жидкая частица вращается с угловой скоростью как «квазитвердая» или «замороженная» частица. В отношении поступательного и вращательного движения можно считать частицу твердой, двигающейся поступательно со скоростью и вращающейся как твердое тело с угловой скоростью . В механике твердого тела эти утверждения справедливы для всего тела, в гидрогазодинамике это относится только к локальному объему выделенной жидкой частицы.

Линейная деформация частицы возникает из-за различия скоростей, направления которых совпадают с направлениями ребер.

Разность скоростей жидкости в точках А и D в направлении оси х равна

.

За время dt ребро АD удлинится на величину

.

Относительное удлинение ребра составит

.

Скорость удлинения параллелепипеда вдоль оси х равна

.

За время dt объем параллелепипеда вследствие удлинения ребра АD увеличится на величину

.

Аналогично для других осей

,

,

,

.

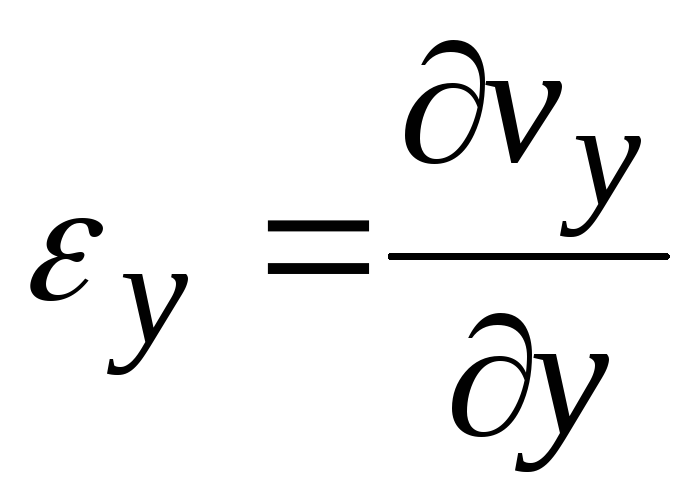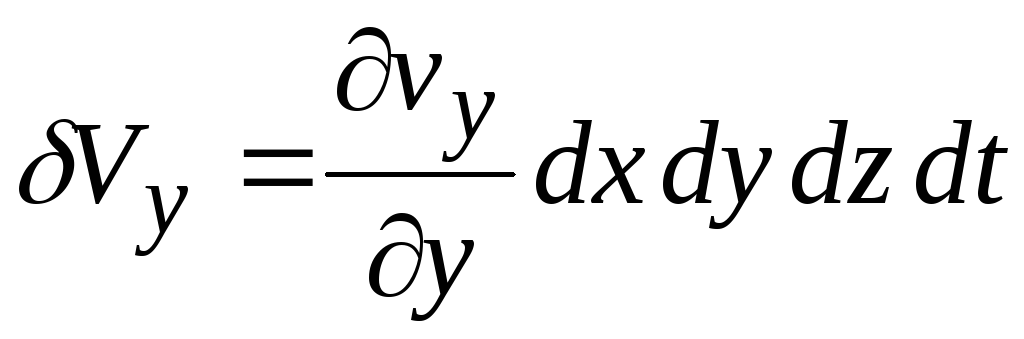Общее изменение объема частицы составит

.

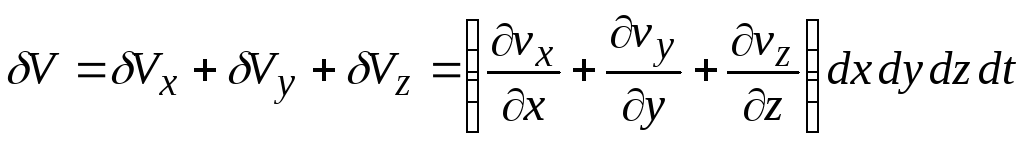Относительное изменение объема частицы за время dt равно

.

Скорость изменения относительного объема частицы

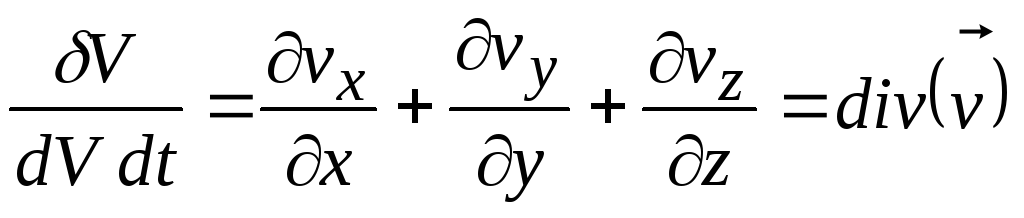. (8.13)

Если объем частицы не меняется, то .

Скорость линейных деформаций частицы определяется величинами 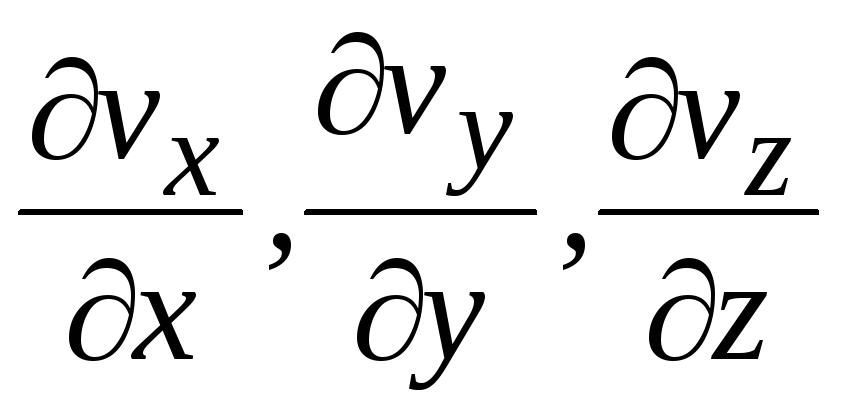. Скорость угловых деформаций частицы равна 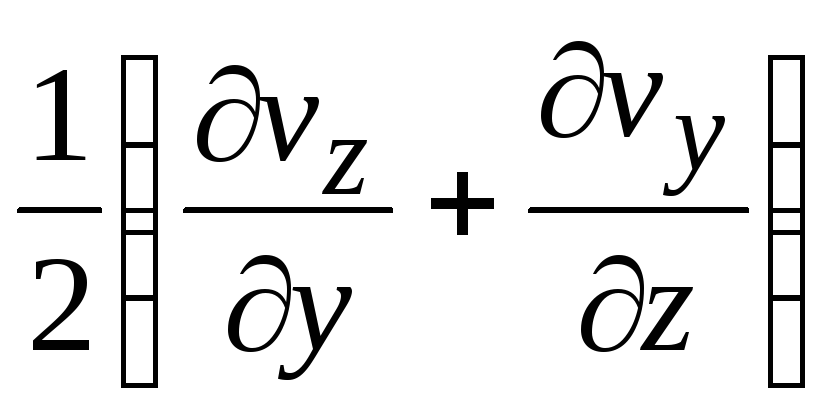, , 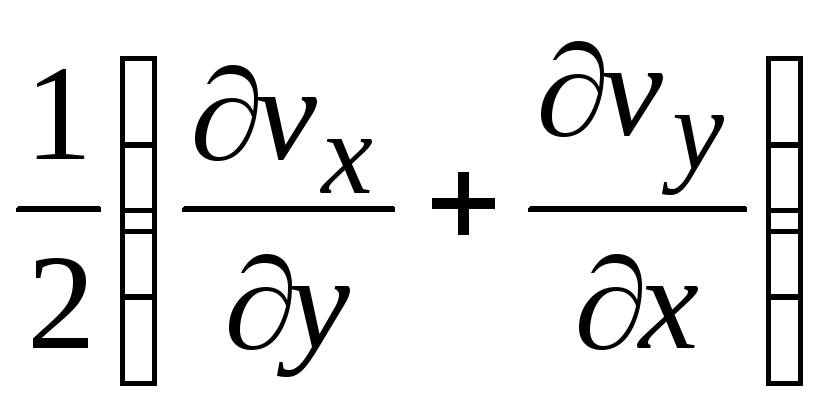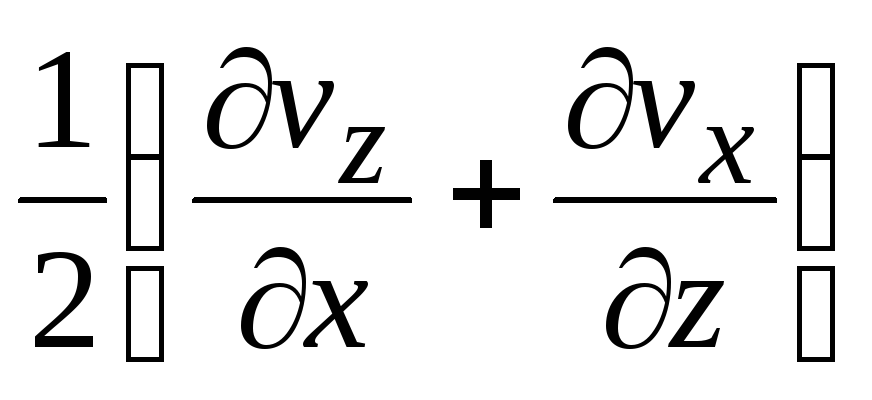. Эти величины обычно записываются в виде матрицы

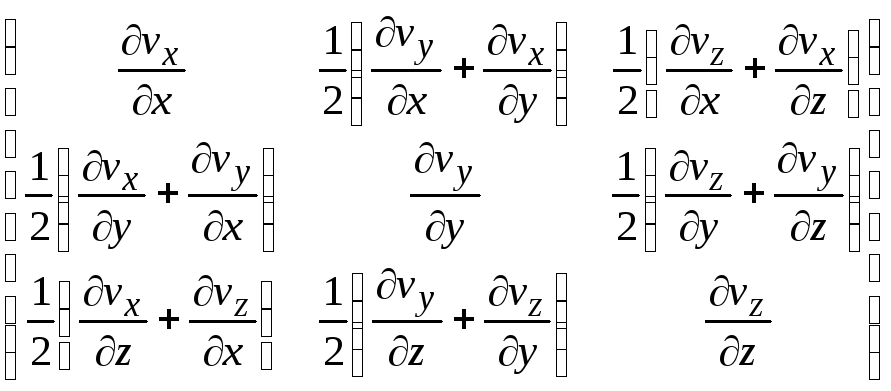. (8.14)

Эта матрица называется матрицей скоростей деформации или тензором скоростей деформации. Матрица симметрична, компоненты зеркально расположенные относительно главной диагонали, равны между собой и поэтому среди девяти элементов матрицы только шесть отличаются друг от друга.

Представленный анализ движения жидкой частицы обобщает первая теорема Гемгольца:

Движение элементарного объема жидкой среды можно в каждый момент времени представить себе разложенным на:

1. квазитвердое движение со скоростью, равной сумме поступательной скорости какой-либо отдельной частицы, заключенной в этом объеме, и вращательной скорости, соответствующей угловой скорости 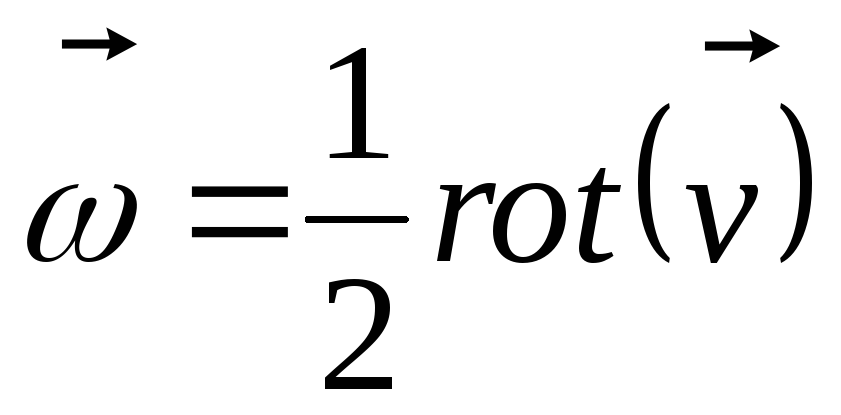, и

2. деформационное движение, определяемое тензором скоростей деформаций, элементы которого задаются матрицей (5.14).

Основной смысл первой теоремы Гемгольца заключается в установлении связанности между собой отдельных составляющих движения элементарного объема, зависящих от заданного поля скоростей. Вращение элементарного объема и его деформационное движение не могут быть произвольными, не зависящими друг от друга и поступательного движения объема. Они связаны между собой совершенно определенными количественными соотношениями, выражающимися через пространственные производные, вычисляемые по заданному полю скоростей.

Лекция 9. ВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ

Вихревые линии и трубки

Вихревые движения в природе наблюдаются часто и могут быть легко обнаружены. Особенно заметно это при обтекании водой различных препятствий или при движении в воде катера. Наблюдаемые в атмосфере смерчи и циклоны также являются вихрями. Мелкие вихри в воздухе или воде создают турбулентную структуру потока, в котором возникают пульсации скоростей, давления, температуры, примесей.

Ранее было показано, что вращательное движение жидких частиц характеризуется угловыми скоростями, значения которых могут быть рассчитаны по (8.5) – (8.7). Это означает, что в каждой точке пространства вращение жидких частиц может быть охарактеризовано вектором угловой скорости , величина которого равна

. (9.1)

Следовательно, подобно тому как было представлено поле скоростей потока жидкости в виде бесчисленной системы векторов линейной скорости , огибающие которых являлись линиями тока, можно также представить поле векторов угловой скорости , называемое также полем вихрей.

Здесь следует обратить внимание на особенности терминологии. Обычно под вихрем понимают круговое движение жидкости или газа, т.е. движение, обладающее угловой скоростью . В математике термину «вихрь» соответствует понятие «ротор», для которого

.

В дальнейшем под вихревым полем будем иметь в виду поле угловых скоростей с векторами . Каждый из векторов в той же степени, что и вектор , характеризует местное вращение жидкости.

Д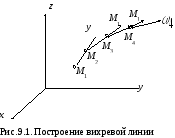опустим, как это показано на рис.9.1, в данный момент времени в некоторой точке пространства М₁ вектор угловой скорости местного вращения равен .

Возьмем в этот же момент времени на этом векторе близкую к точке М₁ точку М₂ и построим соответствующий ей вектор угловой скорости . Продолжая это построение, получим ломаную линию М₁, М₂, М₃, М₄,…, которая при стремлении к нулю каждого отрезка превратится в так называемую вихревую линию. Отсюда следует, что вихревой называется линия, в каждой точке которой в данный момент времени вектор угловой скорости совпадает с касательной к этой линии.

Так как по определению вектор угловой скорости перпендикулярен плоскости вращения, то вихревая линия является мгновенной осью вращения частиц жидкости, которые в данный момент расположены на ней.

Представим себе элементарные объемы жидкости в виде бусинок с заранее проделанными в них отверстиями для продевания нитки. Здесь вихревая линия играет роль нитки.

По аналогии с линией тока дифференциальное уравнение вихревой линии имеет вид

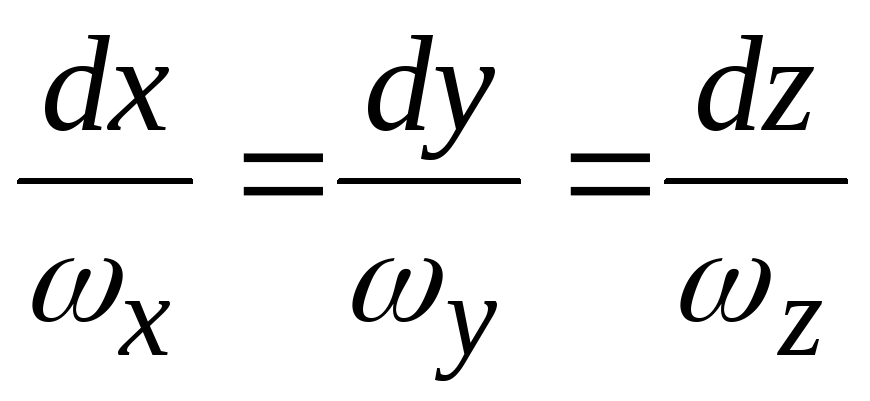. (9.2)

Представим пространство, непрерывно заполненное вихрями и, соответственно, вихревыми линиями. Выделим в пространстве малый замкнутый контур С и проведем через него вихревые линии. Совокупность этих линий образует так называемую вихревую трубку, а объем жидкости, заключенный в ней, представляет собой элемент вихря, называемый вихревым шнуром.