Равновесие жидкости при наличии негравитационных массовых сил

Пусть сосуд, частично заполненный жидкостью, движется в горизонтальном направлении вдоль оси х с ускорением а (рис.3.4).

В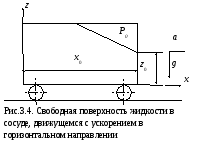 этом случае дополнительно к массовой силе тяжести возникает сила инерции , направленная против оси х. Из (3.6) получим

.

Интегрируя это уравнение, имеем , где постоянная интегрирования С находится из условия: . Отсюда . Окончательно давление в любой точке жидкости определится по формуле

. (3.16)

Уравнение поверхностей равного давления

(3.17)

определяет множество параллельных плоскостей, наклоненных к горизонтали под углом α, тангенс которого равен

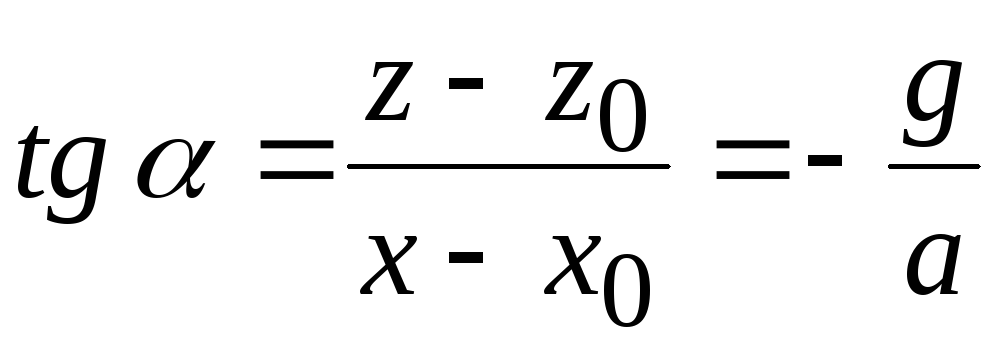. (3.18)

Рассмотрим равновесие жидкости, покоящейся относительно сосуда, который равномерно вращается вокруг вертикальной оси с угловой скоростью  (рис.3.5). На жидкость действуют сила тяжести, направленная вниз, и центробежная сила, направленная по радиусу от оси к стенкам сосуда. Проекции массовых сил на координатные оси равны

Уравнение (3.6) принимает вид

.

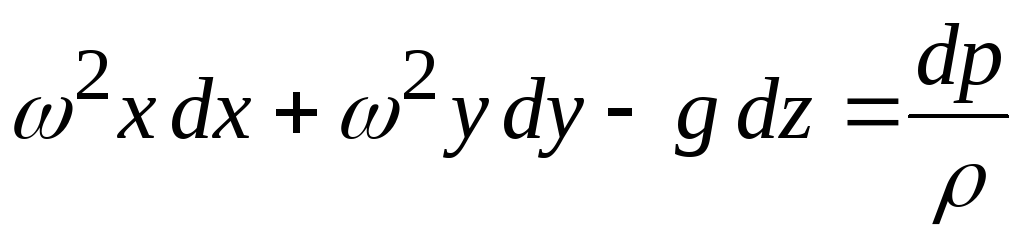После интегрирования получаем

.

Постоянная интегрирования С находится из условий:

,

откуда .

Гидростатическое давление в жидкости равно

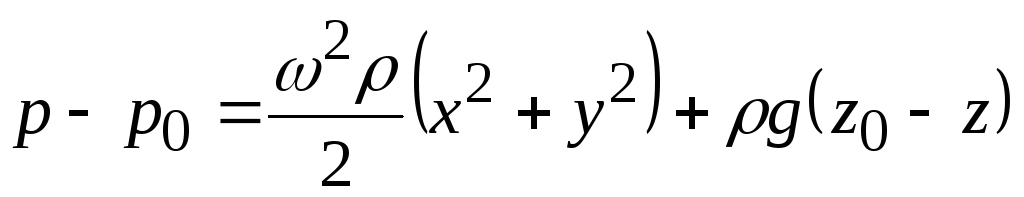. (3.19)

Уравнение поверхностей уровня

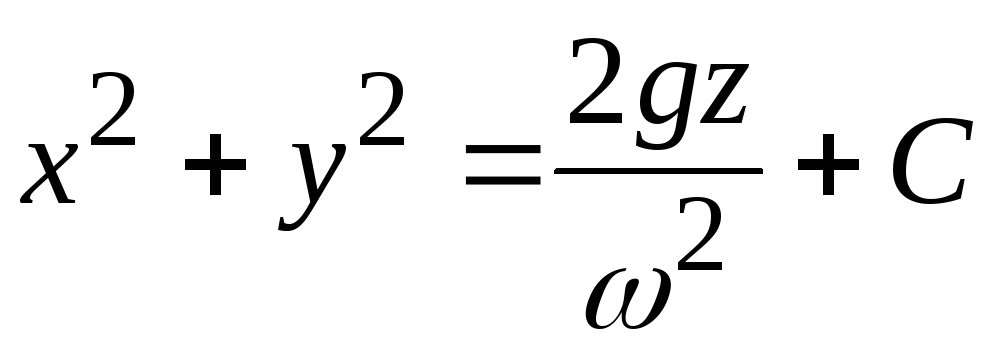(3.20)

является уравнением параболоида вращения.

Лекция 4. Давление жидкости на стенки сосудов

Эпюра гидростатического давления

Эпюрой называется графическое изображение распределения гидростатического давления в плоскости рассматриваемой поверхности, выполненное в определённом масштабе.

При построении эпюры пользуются уравнением распределения давления в покоящейся жидкости

, (4.1)

где h - глубина погружения, отсчитываемая от свободной поверхности жидкости.

Представим сосуд, в котором находится жидкость с удельной плотностью . Высота жидкости в сосуде, как показано на рис.4.1, составляет Н, на свободную поверхность действует давление Р₀

Зависимость (3.1) является уравнением прямой линии. На свободной поверхности при h = 0 избыточное гидростатическое давление отсутствует, полное давление равно Р₀. На дне сосуда при h = H избыточное гидростатическое давление равно gH, полное давление равно Р₀+gH. Давления на глубине можно определить по длине прямой, проведенной на высоте h от вертикальной линии, соответствующей давлению Р=0 до пересечения с прямой линией, соединяющей точки, характеризующие давление на свободной поверхности жидкости и на дне сосуда.

Из рис.4.1 следует, что эпюра избыточного гидростатического давления представляет собой прямоугольный треугольник, а эпюра полного давления – трапецию.

Давление жидкости на плоскую стенку

Используя основное уравнение гидростатики, можно найти силу давления жидкости на различные поверхности. Эта задача имеет большое практическое значение при расчетах гидротехнических сооружений, резервуаров, предохранительных клапанов в технологических аппаратах.

Рассмотрим резервуар с вертикальными и наклонными стенками и плоским дном.

Левая и боковые стенки резервуара вертикальны, правая наклонена к горизонтали под углом , расстояние между правой и левой стенками на дне равно А, глубина резервуара равна Н, а ширина – В. Предположим, что резервуар полностью заполнен жидкостью с плотностью .

Рассмотрим избыточное давление на правую наклонную стенку. Поверхностное давление учитывать не будем, так как оно, действуя через жидкость на стенку слева, полностью уравновешивается атмосферным давлением, действующим на стенку справа.

Выделим находящуюся на глубине h бесконечно малую горизонтальную полоску высотой dℓ. Ввиду малой высоты выделенного элемента гидростатическое давление во всех его точках можно считать одинаковым и равным . Элементарная сила избыточного давления на полоску будет равна

, (4.2)

где представляет собой элемент площади эпюры гидростатического давления.

Площадь самой стенки можно представить состоящей из элементарных полосок, на каждую из которых передается со стороны жидкости давление dP, которое непрерывно изменяется по мере изменения глубины h, но всегда направлено перпендикулярно плоскости стенки.

Сила давления жидкости на стенку будет равна сумме непрерывно изменяющихся элементарных сил, т. е. интегралу

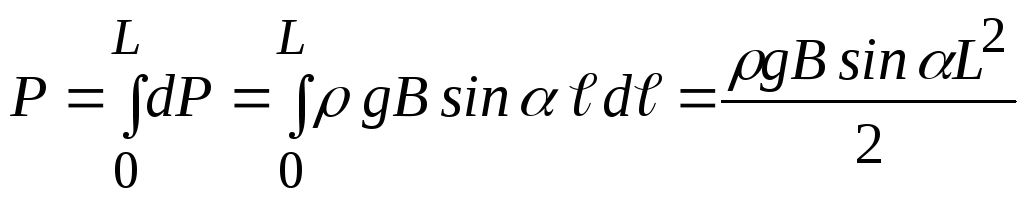. (4.3)

Произведение BL представляет собой площадь стенки, а комплекс равен половине глубины резервуара. Отсюда

. (4.4)

Силу давления жидкости на плоскую прямоугольную стенку можно также рассматривать как произведение площади эпюры гидростатического давления на ширину стенки.

Сила давления на вертикальную стенку при =90 равна

,

Сила давления на дно резервуара

.

Формула (3.4) справедлива только для случая, когда ширина стенки постоянна по всей глубине резервуара. Если это условие не выполняется, то величину В в формуле (3.3) нельзя выносить за знак интеграла. В итоге получаем

.

Величина представляет собой площадь элемента поверхности на глубине h. Интеграл

,

где ℓ_с – расстояние от поверхности до центра тяжести стенки. Отсюда сила давления жидкости на плоскую фигуру равна произведению площади стенки на гидростатическое давление в центре тяжести стенки.

Давление, обусловленное весом жидкости, неравномерно распределяется по площади стенки: чем глубже расположена точка на поверхности стенки, тем большее давление она испытывает. Поэтому точка приложения силы давления, т.е. центр давления, находится ниже центра тяжести стенки.