Функция тока плоского течения

В практических задачах гидромеханики двумерных потоков широчайшее применение находит понятие о функции тока. Рассмотрим двумерный поток и ограничимся несжимаемой жидкостью.

Как было показано, для плоского течения дифференциальное уравнение линии тока имеет вид

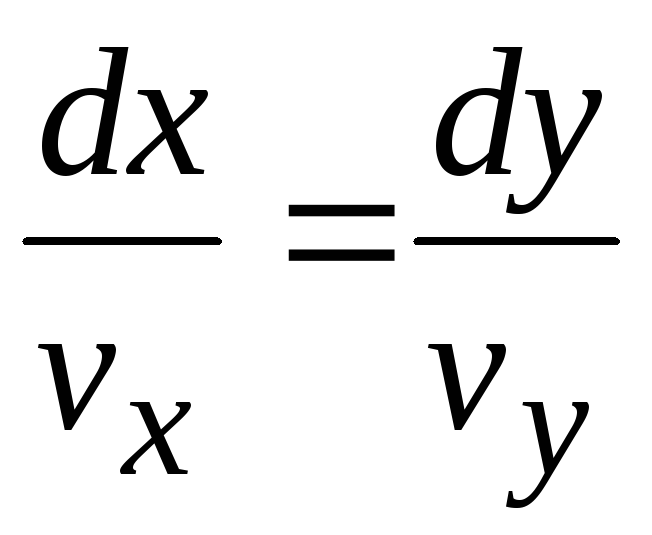
или

. (10.10)

Плоское течение или в общем случае двумерное течение жидкости обладает той особенностью, что для него можно ввести функцию тока :

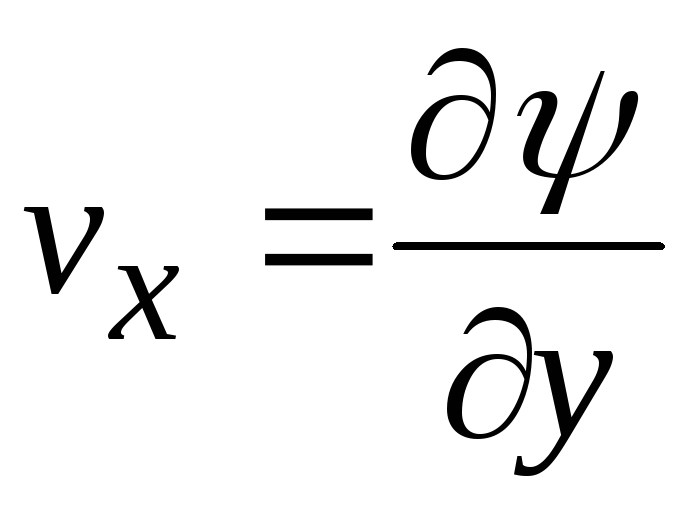, (10.11)

. (10.12)

Подставляя (10.11) и (10.12) в (10.10), получим

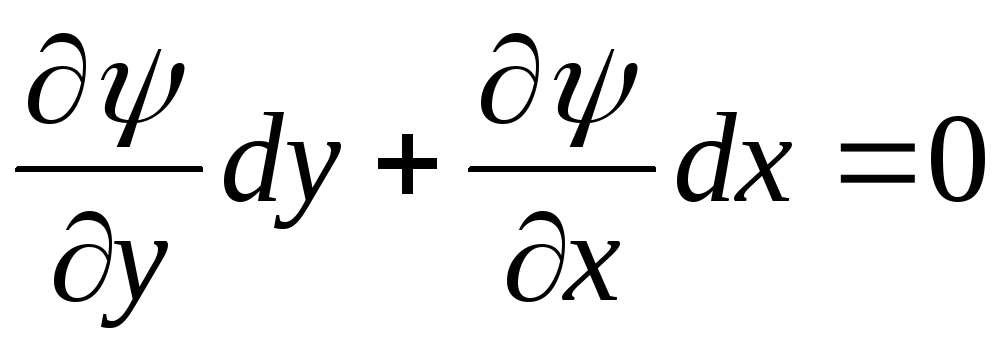. (10.13)

Так как по условию (10.3) смешанные производные равны

,

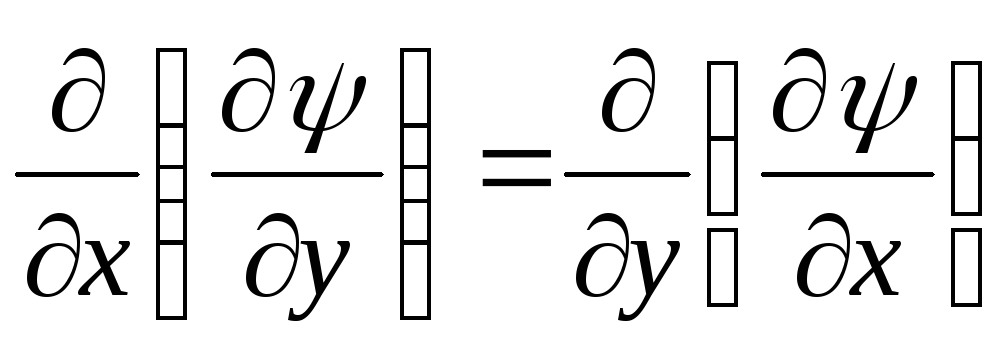то (10.13) является полным дифференциалом и для линии тока можно записать

или

, (10.14)

где С – произвольная постоянная.

Уравнение (10.14) является семейством линий тока. Каждому конкретному значению С соответствует своя линия тока. Изменяя значение С, будем получать различные линии тока.

Для плоского потенциального течения , т.е.

,

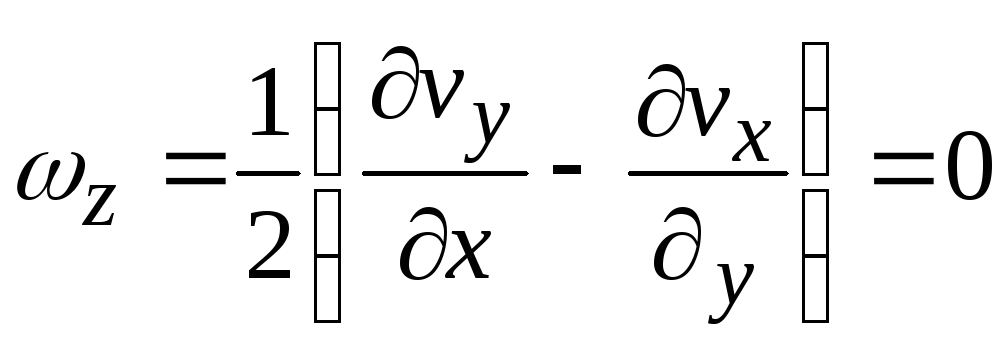откуда получаем уравнение Лапласа

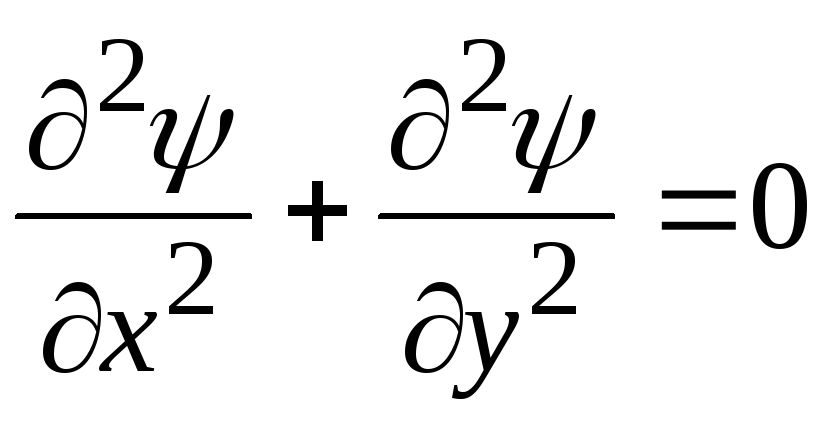. (10.15)

Следует отметить, что потенциал скорости существует только в потенциальном потоке, т.е. в потоке без вихрей. Функция тока существует также и в вихревом потоке, но определена только для двумерного потока.

Если потенциалу скорости задать некоторое фиксированное значение С, то получим семейство линий

, (10.16)

обладающих тем свойством, что вдоль каждой линии потенциал скорости остается постоянным. Такие линии называются эквипотенциальными. В потенциальном потоке скорость жидкости направлена в сторону наибольшего изменения потенциала  и по этой причине скорость перпендикулярна линиям постоянного потенциала.

Линии постоянного значения функции тока совпадают с линиями тока, вдоль которых направлена скорость потока. По этой причине в потенциальном плоском установившемся потоке семейство линий тока и семейство эквипотенциальных линий взаимно перпендикулярны или ортогональны. Сетка кривых и называется гидродинамической сеткой. Вид ее показан на рис. 10.1.

Так как в потенциальном поле

,

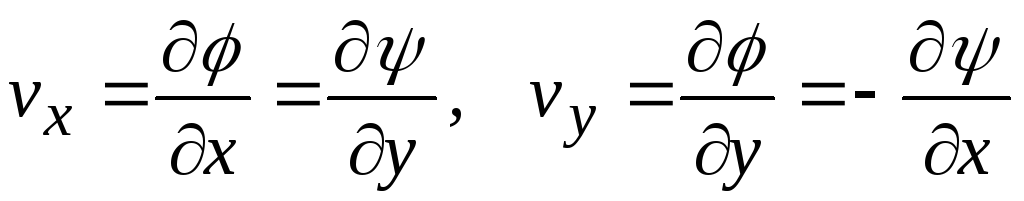то

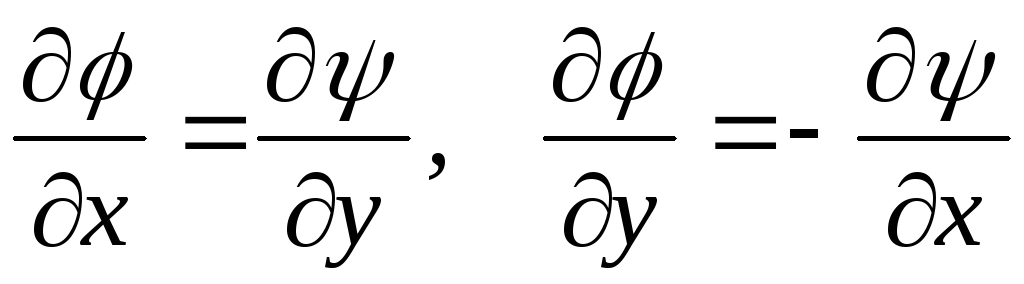. (10.17)

Выражения (10.17) называются соотношениями Коши-Римана.

Рассмотрим гидромеханический смысл функции тока, для чего проведем две достаточно близко расположенные линии тока, как показано на рис.6.2.

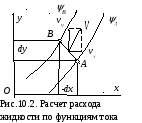
Возьмем на линиях тока точки А и В. Разложим скорость потока по координатным осям и вычислим расход жидкости между точками в направлениях осей:

.

Общий расход составит

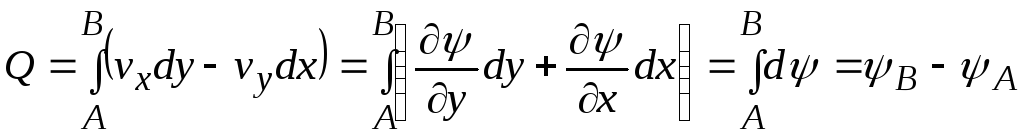. (10.18)

Отсюда следует, что объемный расход между двумя линиями тока равен разности значений функций тока на этих линиях. Если контур замкнут, т.е. точки А и В совпадают, и функция тока является однозначной, то расход жидкости через такой контур равен нулю. При неоднозначности функции тока, когда в нутрии контура имеется источник жидкости или сток, .

Лекция 11. Методы расчета потенциальных потоков

Для нахождения потенциала скорости и функции тока необходимо проинтегрировать уравнения Лапласа при заданных граничных условиях, что является достаточно сложной задачей. Существует метод, позволяющий определить значения потенциала и функции тока без интегрирования уравнений Лапласа. Общая идея метода сводится к следующему: сначала задаются некоторой функцией, которая удовлетворяет уравнению Лапласа, а затем выясняют, чему соответствует гидромеханическая сетка движения.

Пример 1. Пусть выражение для потенциала скорости имеет вид

,

где a и b – некоторые действительные числа.

Найдем проекции скорости на координатные оси:

.

Проверим, удовлетворяет ли выражение для потенциала уравнению Лапласа.

.

Выражение для потенциала скорости соответствует уравнению Лапласа. Скорости потока в направлении координатных осей и постоянны, поток двигается с постоянной скоростью. Полная скорость потока

.

Выясним, что представляют собой линии тока. Так как

,

то после интегрирования имеем

. (11.1)

Для линии тока справедливо соотношение . Приравнивая (11.1) некоторой постоянной, получим

или .

Это уравнение семейства параллельных прямых, наклоненных под углом к оси х. Вид гидродинамической сетки показан на рис. 11.1.

Пример 2. Пусть потенциал скорости задан выражением

,

где а – некоторое действительное число, при этом а >0.

Определяем проекции скорости

.

Проверяем, удовлетворяет ли выражение для потенциала уравнению Лапласа

.

Выражение соответствует уравнению Лапласа.

Определяем вид функций тока

.

После интегрирования имеем

. (11.2)

Произвольная постоянная в данном случае нас не интересует. Приравнивая (11.2) некоторой постоянной, получим

или .

Получили семейство кривых, описываемых уравнением

.

Отсюда следует, что линии тока представляют собой семейство гипербол с асимптотами, являющимися осями координат. При С₁>0 или x>0, y>0, или x<0, y<0 ветви гипербол располагаются в первой и третьей четвертях, в другом случае – во второй и четвертой четвертях. Если C₁=0, то линиями тока являются оси координат х=0, у=0.

В любом случае в начале координат . Точка потока, в которой скорость равна нулю, называется критической точкой.

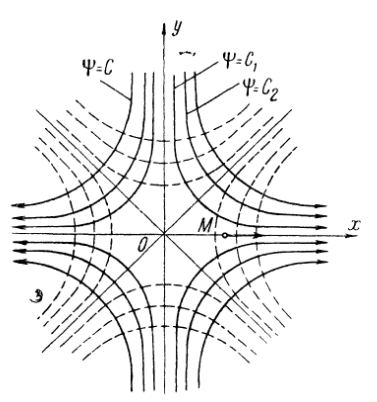
Если потенциал скорости приравнять некоторой постоянной величине, то получим семейство эквипотенциальных линий

.

Это уравнение описывает семейство гипербол с асимптотами, являющимися биссектрисами координатных углов и ортогональных к гиперболам .

Если положительные части осей х и у принять за твердые стенки, то получим картину обтекания потоком прямого угла. Гидромеханическая сетка потока показана на рис.11.2.

Пример 3. Источник и сток на плоскости. Под источником и стоком на плоскости понимают точку, из которой происходит истечение или втекание жидкости.

Пусть потенциал скорости задан в виде

,

где а – некоторое действительное число. При а >0 движение жидкости происходит из начала координат к периферии, в центре координат располагается источник жидкости. При a <0 поток движется из периферии к центру координат, в центре координат происходит сток жидкости.

Для осесимметричного течения более удобными являются цилиндрические координаты с осями , , z. Для двумерного потока координата z исчезает. Так как , то в полярных координатах выражение для потенциала скорости принимает вид

.

Определяем проекции скорости на координатные оси:

,

.

Отсюда следует, что скорость жидкости и линии тока направлены по радиусам от центра при источнике и к центру при стоке.

Уравнение Лапласа в цилиндрических координатах имеет вид

.

Для плоского течения в полярных координатах , 

.

Проверяем, удовлетворяет ли выражение для потенциала уравнению Лапласа

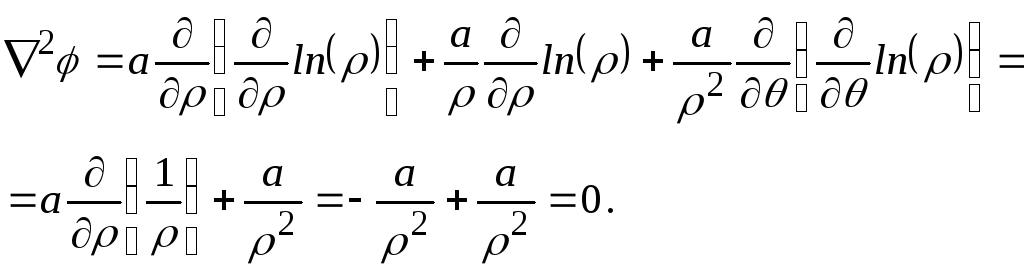
Выражение соответствует уравнению Лапласа.

Уравнение прямой линии в полярных координатах, проходящей через центр координат

.

Выражение для функции тока, постоянной на линии тока

где С – некоторая величина.

Определим значения параметров в выражениях для потенциала скорости и функции тока. Эквипотенциальные линии соответствуют выражению , т.е. представляют собой концентрические окружности. Примем, что толщина слоя жидкости по оси z равна 1. Тогда на радиусе  площадь сечения для прохода жидкости будет равна

.

При объемном расходе жидкости Q на радиусе  будет равна

.

Отсюда видно, что скорость потока обратно пропорциональна радиусу, т.е. расстоянию от центра источника или стока. В начале координат скорость обращается в бесконечность, что реально недостижимо.

Так как , то и .

На любом радиусе расход жидкости через эквипотенциальную линию, т.е. окружность равен Q, при этом через сектор с углом d расход будет равен

.

О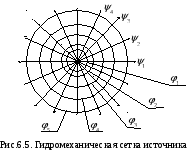тсюда .

Гидромеханическая сетка для источника показана на рис.11.3.