Лекция 12. Наложение потенциальных потоков

Предположим, что имеются два потока с известными потенциалами скорости ₁ и ₂, удовлетворяющими уравнению Лапласа. Из теории линейных дифференциальных уравнений, к которым принадлежит и уравнение Лапласа, известно, что сумма частных решений этих уравнений также является их решением. Это означает, что потенциал , образованный как, также будет удовлетворять уравнению Лапласа, т.е. будет описывать какой-то новый поток, имеющий потенциал . Из этого следует, что можно получить новый поток путем сложения (наложения) уже известных. Следует обратить внимание на то, что собственно наложение потоков здесь не производится, а речь идет о сложении потенциалов скорости уже известных течений. Скорость в каждой точке нового потока является суммой скоростей первоначальных потоков.

Пример 4. Совместное течение источника и стока. Комбинация источника мощностью Q и стока мощностью –Q, помещенных на бесконечно малое расстояние друг от друга, называется диполем или дублетом. Потенциал диполя, используя метод наложения, можно записать в виде

.

Проведем ось х по линии, соединяющей источник и сток, таким образом, чтобы источник находился от начала координат на расстоянии -, а сток – на расстоянии . Отсюда расстояние между источником и стоком равно 2. Возьмем согласно рис.12.1 произвольную точку М с координатами х, у. Расстояния до точки М:

,

.

Потенциал скорости в точке М

.

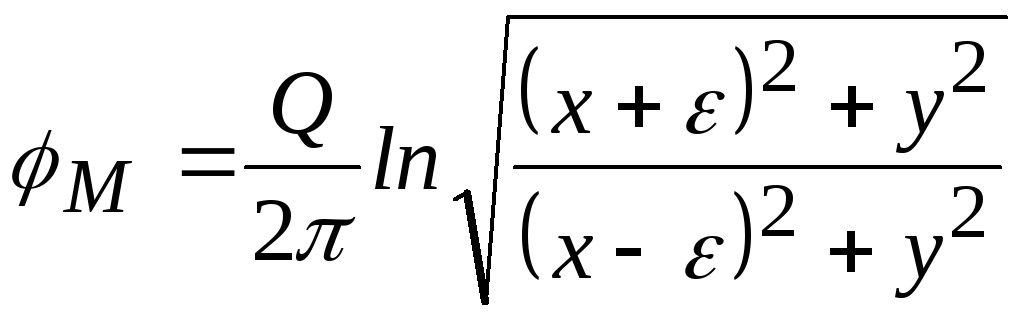Функции тока для источника и стока

,

.

Отсюда

.

Из рис.6.6 следует

.

Отсюда

.

Далее находим

.

Следовательно, функцию тока можно представить в виде

.

Выражение раскладывается в виде бесконечного ряда

.

Так как величина  мала, то z с увеличением степени быстро уменьшается. Поэтому ограничимся только первой степенью и примем

.

Тогда

.

Проводя аналогичные действия с выражением для потенциала скорости, можно показать, что

.

Будем сближать источник и сток таким образом, чтобы произведение оставалось постоянным. Величина D называется моментом диполя.

Переходя к пределу при , получим

,

.

Найдем линии тока и эквипотенциальные линии для течения от диполя. Для нахождения линий тока приравняем функцию  постоянной величине С:

,

откуда

.

Это выражение описывает семейство окружностей с центрами на оси у, касающихся оси х в центре координат. Таким образом, жидкость по указанным окружностям вытекает из начала координат и вновь в него втекает.

В этом случае расход жидкости через произвольный замкнутый контур, окружающий диполь, равен нулю.

Совокупность эквипотенциальных линий

будет представлять семейство окружностей, ортогональных линиям тока, с центрами на оси х, касающихся оси у в начале координат. Гидромеханическая сетка течения показана на рис. 6.7.

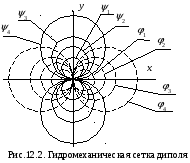
Пример 5. Течение в плоском вихре.

Для плоского источника потенциал скорости и функция тока описываются зависимостями

, .

Рассмотрим плоский поток, в котором потенциал скорости и функция тока поменяются местами:

, .

Здесь Q >0 – некоторая постоянная, физический смысл которой для нового потока следует определить.

Для выявления характера линий тока приравняем значение функции тока некоторой постоянной величине. Будем иметь

.

Полученная зависимость описывает семейство концентрических окружностей с центром в начале координат. Найдем направление движения в полярных координатах:

,

.

Следовательно, в точке М скорость направлена по касательной к окружности радиуса , и точка М совершает по ней движение в сторону возрастания угла , т.е. против часовой стрелки. Таким образом, все точки жидкости двигаются по концентрическим окружностям с постоянной для данной окружности скоростью. Скорость жидкости на окружности обратно пропорциональна радиусу окружности.

Такое движение жидкости называется плоским вихревым движением, а начало координат – вихревой точкой или плоским вихрем. Движение соответствует прямолинейному бесконечно длинному вдоль оси z вихрю, вызывающему вращение жидкости по концентрическим окружностям, перпендикулярным оси z.

Выясним физический смысл постоянной Q. Для этого вычислим значение циркуляции скорости в рассматриваемом потоке

.

Отсюда . Тогда , .

Приравняв потенциал скорости некоторой постоянной C, найдем вид эквипотенциальных линий:

.

Это семейство прямых, проходящих через центр координат и ортогональных линиям тока.

Примем одну из линий тока, например, окружность радиуса =₀ за твердую границу, что не нарушит характера потока, и будем рассматривать движение жидкости вне этой окружности. Тогда получим так называемое чисто циркуляционное обтекание бесконечно длинного круглого цилиндра радиусом ₀, при котором все линии тока являются концентрическими этому цилиндру окружностями. Окружная скорость в любой точке вне цилиндра равна

.

Максимального значения скорость потока достигает на поверхности цилиндра

.

По мере удаления от цилиндра скорость будет убывать по закону

.

Характер изменения скорости при циркуляционном обтекании круглого цилиндра показан на рис. 12.3.

Пример 6. Бесциркулярное обтекание круглого цилиндра.

Течение диполя представляется абстрактным, однако в комбинации с другими потоками дает очень важные практические результаты. Рассмотрим течение, возникающее при наложении прямолинейного поступательного течения на диполь с центром, расположенным в начале координат. Пусть поток движется вдоль оси х со скоростью v_x=1, а момент диполя D = 2. Тогда потенциал скорости поступательного движения будет равен

,

а функция пока будет иметь выражение, соответствующее прямым, параллельным оси х:

.

У диполя эти характеристики будут равны

, .

У сложного потока эти характеристики будут иметь следующий вид:

, .

Найдем линии тока, для чего приравняем функции тока постоянную величину:

.

Отсюда

.

Из этого следует, что линии тока представляют собой семейство кривых третьего порядка. Для выяснения картины течения найдем нулевую линию тока, соответствующую С = 0. Для нулевой линии тока получаем два уравнения:

Первое уравнение дает решение в виде оси х, второе уравнение описывает окружность нулевого радиуса с центром в начале координат. Так как линии тока непроницаемы для жидкости, поток движется по касательным к линиям тока, то нулевую, как и любую другую линию тока, можно представить в виде твердой границы и считать, что внешний поток обтекает бесконечно длинный цилиндр с радиусом, равным единице.

Картина течения показана на рис.12.4. Покажем, что на достаточно большом удалении от цилиндра (на бесконечности) скорость направлена в положительную сторону оси х и равна скорости невозмущенного потока, т.е. как ранее было принято, единице.

Найдем проекции скорости:

,

.

Перейдем к полярным координатам:

,

.

В пределе при получаем .

Точки пересечения А и В нулевых линий тока на цилиндре являются критическими точками, т.к. скорость в них обращается в нуль. Представим потенциал скорости в полярных координатах:

.

Найдем проекции скорости в произвольной точке пространства

,

.

На цилиндре, т.е. при  =1 радиальная скорость v_=0, т.е. течение вокруг цилиндра безотрывное, в каждой точке поверхности скорость жидкости направлена по касательной. Окружная скорость v_ = -2sin. В точках А и В, где угол равен соответственно скорости равны нулю, т.е. эти точки действительно являются критическими. Максимальная скорость достигается в точках пересечения оси у с поверхностью цилиндра, т.е. при . Она равна удвоенной скорости невозмущенного потока независимо от размеров цилиндра.

Лекция 13. ОСНОВНЫЕ УРАВНЕНИЯ ГИДРОГАЗОДИНАМИКИ

Уравнение неразрывности

Уравнение неразрывности представляет собой закон сохранения массы движущейся среды. При отсутствии источников и стоков в установившемся движении через каждое поперечное сечение трубки тока должна протекать в единицу времени одна и та же масса жидкости. Пусть s есть поперечное сечение трубки тока, - средняя скорость в этом сечении,  - плотность жидкости в этом сечении. Требование сохранения массы сводится к тому, чтобы во всех поперечных сечениях одной и той же трубки тока величина имела постоянное значение, т.е. чтобы соблюдалось условие

. (13.1)

Для потоков несжимаемой жидкости справедливым оказывается и условие постоянства объемного расхода. Но так как через рассматриваемое сечение трубки тока за данное время не может пройти больший объем, чем через любое другое поперечное сечение, то для установившихся и неустановившихся несжимаемых потоков всегда справедливо уравнение

, (13.2)

откуда имеем

. (13.3)

Отсюда следует

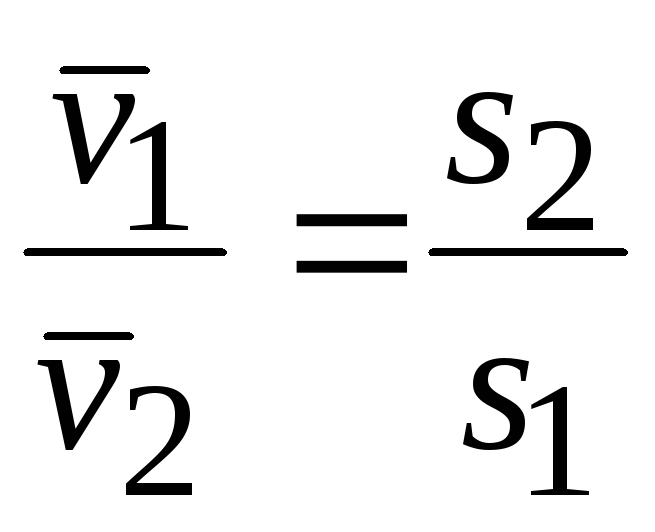, (13.4)

т.е. средние скорости потока обратно пропорциональны площади соответствующих живых сечений.

Для анализа трехмерного течения выделим в потоке жидкости элементарный параллелепипед со сторонами dx, dy, dz (рис. 13.1).

Через левую сторону параллелепипеда в элементарный объем в единицу времени поступает жидкость в количестве . Из параллелепипеда через правую сторону, где скорость уже изменилась и стала равной , а плотность стала равной , в это же время уходит жидкость в количестве 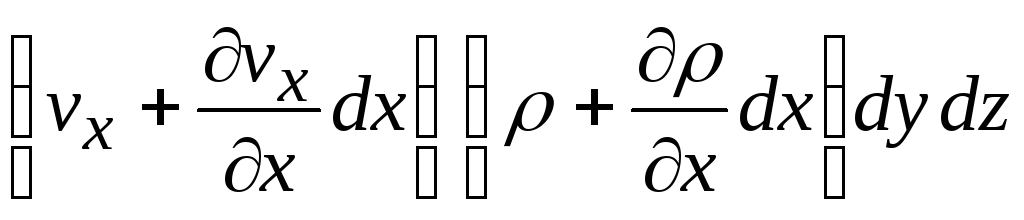. Изменение расхода в направлении оси х равно

.

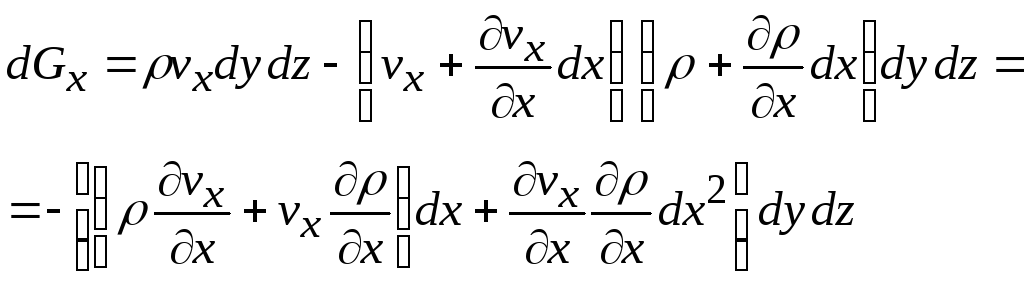Пренебрегая бесконечно малыми второго порядка, получим

. (13.5)

Аналогично для других осей координат

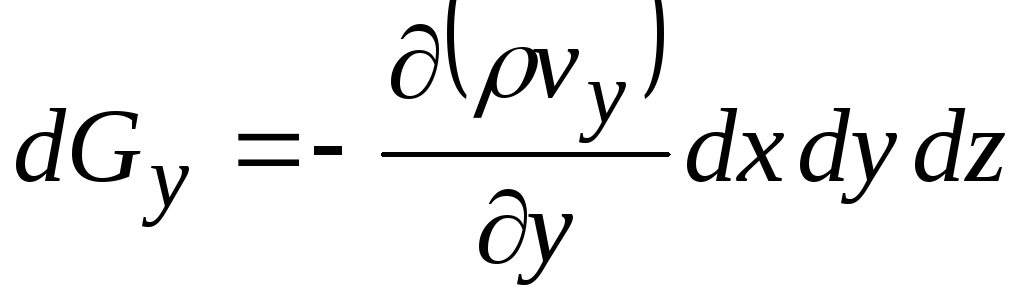, (13.6)

. (13.7)

При установившемся движении несжимаемой жидкости

, (13.8)

откуда

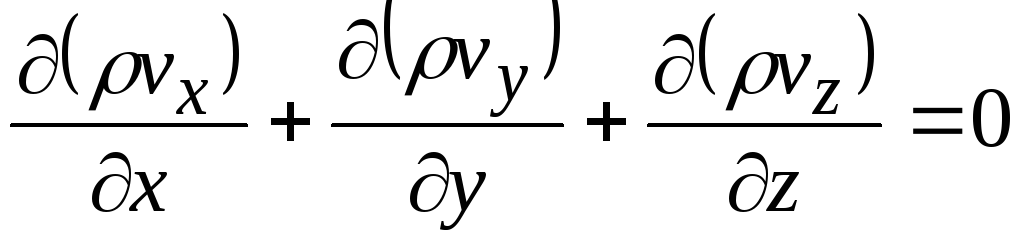. (13.9)

Для неустановившегося сжимаемого потока уравнение неразрывности имеет вид

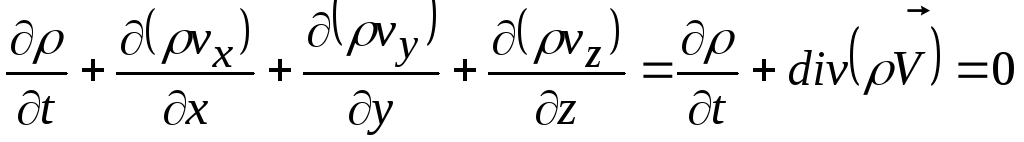. (13.10)

Уравнение (13.10) называется уравнением неразрывности в дифференциальной форме. Его можно записать в виде

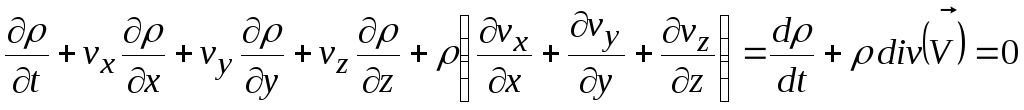. (13.11)

Так как и 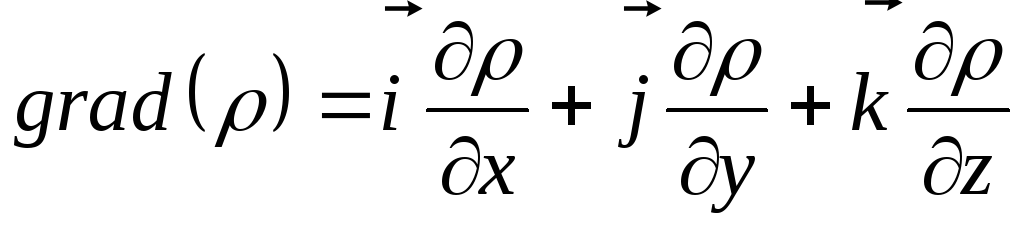, то (13.11) можно представить в виде

(13.12)

или

, (13.13)

а также

. (13.14)

Для установившегося потока имеем

. (13.15)

Для несжимаемой жидкости при  = const

. (13.16)

Градиент скалярной функции  и дивергенция вектора в цилиндрических координатах имеют вид

, (13.17)

. (13.18)

В соответствии с этим уравнение неразрывности в цилиндрических координатах для сжимаемого нестационарного потока принимает вид:

, (13.19)

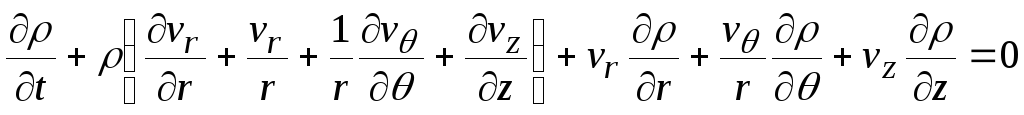(13.20)

или

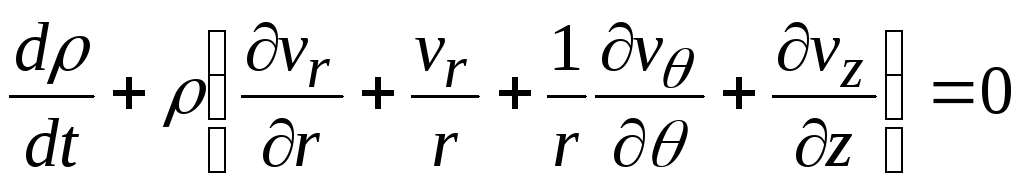. (13.21)

Для стационарного несжимаемого потока имеем

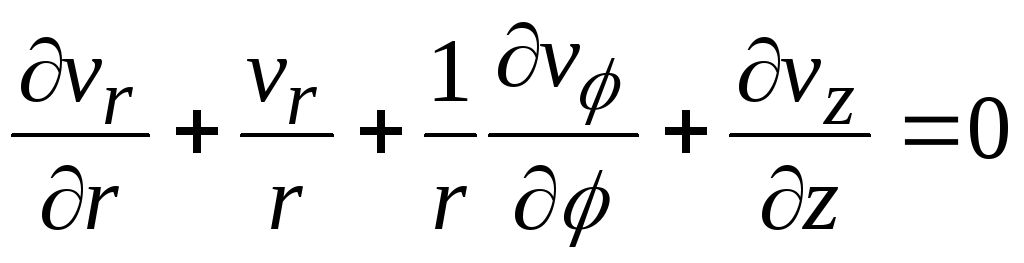. (13.22)

Лекция 14. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ

ИДЕАЛЬНОЙ ЖИДКОСТИ (УРАВНЕНИЯ ЭЙЛЕРА)

Ранее отмечалось, что в покоящейся жидкости два рода сил:

1. силы тяжести и другие массовые силы;

2. поверхностные силы, проявляющиеся в виде разности давлений.

Эти же силы действуют и движущейся жидкости, но к ним присоединяется и трение жидкости, которое следует рассматривать как сопротивление деформации. Жидкости, наиболее важные для техники, в частности вода и воздух, обладают очень малой вязкостью, и поэтому во многих случаях сопротивление, возникающее вследствие трения, очень мало. Поэтому обычно принято основные законы движения жидкостей выводить на основе идеализированного представления о жидкости, лишенной трения, и только потом учитывать, какие изменения вносит трение в идеальное поведение жидкости.

Движение жидкости, как и любого другого тела, подчиняется второму закону Ньютона: ускорение тела прямо пропорционально действующей на тело силе и обратно пропорционально массе тела m. Отсюда можно записать

. (14.1)

Выделим в движущейся жидкости параллелепипед со сторонами dx, dy, dz (рис.14.1).

Объем параллелепипеда равен dx dy dz, а масса жидкости в нем . В направлении оси х на параллелепипед действует массовая сила На левую сторону параллелепипеда действует сила давления , на правую сторону против направления оси х действует сила давления . Ускорение элементарного объема в направлении оси х равно . Подставляя эти выражения в (7.23), получим

.

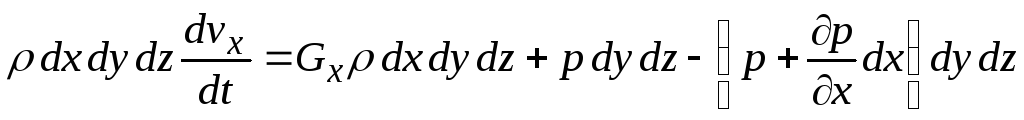Проводя подобные рассуждения для осей y и z и сокращая на , получим систему уравнений

(14.2)

Уравнения (14.2) называются уравнениями Эйлера. В развернутом виде уравнения выглядят следующим образом

Для несжимаемой жидкости ( = const) система уравнений Эйлера имеет четыре неизвестных: . Так как система содержит 3 уравнения, а всего 4 неизвестных, то для замыкания системы к ней добавляется уравнение неразрывности:

.

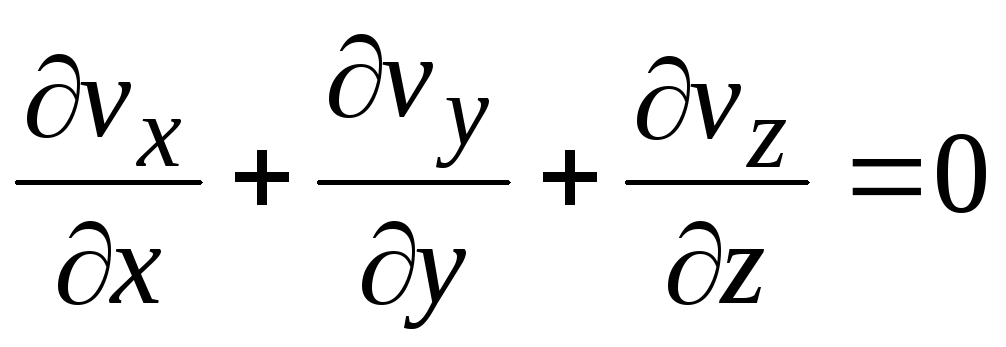Для получения конкретных решений необходимо задать условия однозначности:

1. геометрические размеры расчетной области;

2. физические константы, характеризующие жидкость;

3. начальные значения искомых параметров в начальный момент времени;

4. граничные условия, т.е. значения параметров на границах области.

Система уравнений (7.24) совместно с уравнением неразрывности и условиями однозначности представляет полную математическую постановку задачи.