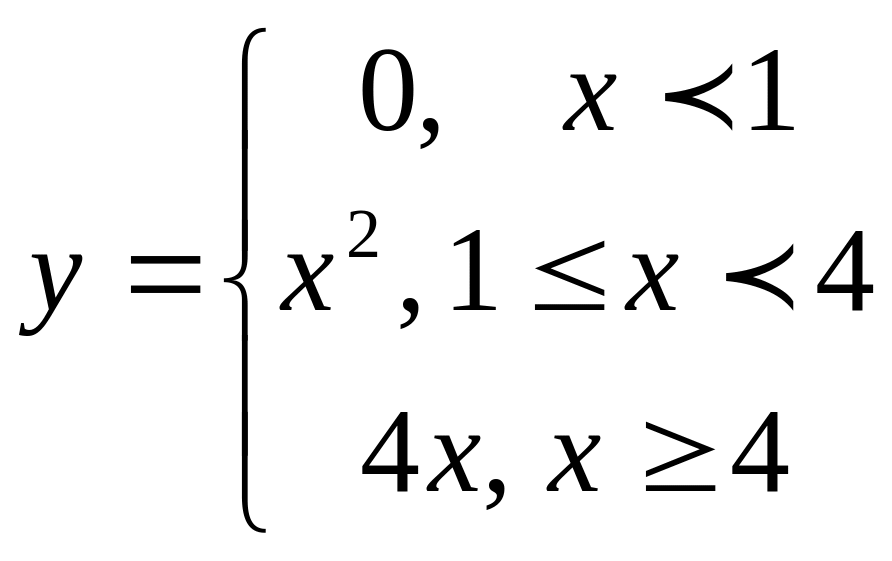- •Введение в предмет
- •Лекция 1.1.
- •Математика, ее история, основные элементы и методы
- •1. Предмет, задачи и содержание курса «Математика»
- •2. История развития математики, ее основные этапы
- •3. Развитие понятия числа. Комплексные числа.
- •Контрольные вопросы
- •Раздел I.
- •Тема 2.
- •1. Понятие системы линейных алгебраических уравнений
- •2. Понятие матрицы, виды матриц
- •3. Определители и их свойства. Формулы Крамера
- •1. Арифметические операции над матрицам
- •1)Сложение матриц
- •2) Вычитание матриц
- •3)Умножение матрицы на число
- •4) Произведение матриц
- •2. Понятие обратной матрицы и метод ее нахождения
- •3. Решение систем линейных алгебраических уравнений матричным методом
- •2. Метод Гаусса решения слау
- •Контрольные вопросы
- •Тема 3.
- •Элементы векторной алгебры и аналитической геометрии
- •Лекция 3.1.
- •Вектора
- •1. Вектор. Линейные операции над геометрическими векторами
- •Проекция вектора на ось. Разложение вектора по ортам координатных осей
- •Действия над векторами в координатной форме
- •Лекция 3.2. Нелинейные операции над векторами. Линейная независимость векторов и базис пространства.
- •2. Линейная зависимость и линейная независимость векторов Лекция 3.3 Аналитическая геометрия на плоскости и а пространстве
- •1. Метод координат на плоскости
- •2. Виды уравнений прямой на плоскости
- •3. Условия параллельности и перпендикулярности прямых на плоскости
- •4. Прямая и плоскость в пространстве
- •Контрольные вопросы
- •Раздел II.
- •Тема 4.
- •1. Множества и операции над ними
- •2. Понятие функции, ее свойства
- •3. Понятие числовой последовательности
- •Лекция 4.2. Предел функции, основные свойства
- •1. Предел числовой последовательности и его свойства
- •2. Понятие предела функции
- •3. Основные теоремы о пределах
- •Лекция 4.3. Бесконечно малые и бесконечно большие функции, их свойства
- •1. Понятие бесконечно малых и бесконечно больших функции, их свойства
- •2. Эквивалентные бесконечно малые функции
- •Раскрытие неопределенностей
- •Лекция 4.4. Замечательные пределы. Непрерывность функций
- •1. Первый замечательный предел
- •Второй замечательный предел
- •Непрерывные функции и их свойства
- •Контрольные вопросы
- •Тема 5.
- •Задачи, приводящие к понятию производной
- •Понятие смысл производной
- •Лекция 5.2. Понятие дифференциала функции и его применение в приближенных вычислениях
- •1. Понятие дифференциала функции, его свойства и геометрический смысл
- •2. Применение дифференциала в приближенных вычислениях
- •Лекция 6.3 Приложение понятия производной
- •Основные теоремы о дифференцируемых функциях
- •Применение производных для вычисления пределов функций (правило Лопиталя)
- •Задания для самостоятельной работы
- •Возрастание и убывание функций. Экстремумы функции
- •Лекция 5.4. Общее исследование функций с помощью производной
- •Контрольные вопросы
- •Тема 6.
- •Дифференциальное исчисление функции нескольких переменных
- •Лекция 6.1.
- •Фнп. Частные производные
- •1.Понятие функции двух и нескольких переменных
- •Лекция 6.2. Приложения понятия частных производных
- •Производная по направлению
- •2. Градиент функции и его применение
- •1. Определение первообразной и неопределенного интеграла
- •2. Непосредственное интегрирование
- •3. Основные методы интегрирования
- •Лекция 7.2. Определенный интеграл и его вычисление
- •Задача о площади криволинейной трапеции
- •Понятие определенного интеграла и его свойства
- •3.Формула Ньютона-Лейбница и основные методы нахождения определенного интеграла
- •Лекция 7.3. Определенный интеграл и его вычисление
- •Понятие несобственного интеграла второго рода
- •Приложения определенного интеграла
- •Контрольные вопросы по теме
- •Тема 8.
- •Дифференциальные уравнения
- •Лекция 8.1.
- •Дифференциальные уравнения первого порядка, их виды и методы решения
- •1. Понятие дифференциального уравнения и его решения
- •2. Дифференциальное уравнение первого порядка. Задача Коши
- •3. Основные виды дифференциальных уравнений первого порядка
- •Лекция 8.2. Дифференциальные уравнения высших порядков
- •1. Дифференциальные уравнения второго порядка, допускающие понижения порядка
- •2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные дифференциальные уравнения (лоду) второго порядка с постоянными коэффициентами
- •1. Понятие числового ряда, его сходимость и сумма
- •1.2. Примеры числовых рядов.
- •Лекция 9.2. Степенной ряд и его область сходимости.
- •2. Степенной ряд, вид его области сходимости
- •Контрольные вопросы
2. Понятие функции, ее свойства
В самом общем понимании функция-это зависимость между переменными, где переменной называется величина, которая может принимать различные числовые значения. Введем строгое определение функции.
Функция y=f(x)
зависимость f,
при которой каждому x![]() D
ставится в соответствие единственное
значение y
E.
D
ставится в соответствие единственное
значение y
E.
Записывают:
y=f(x),
![]() ,
x-
аргумент или независимая переменная;
y-
функция или зависимая переменная.
,
x-
аргумент или независимая переменная;
y-
функция или зависимая переменная.
Например, функция
![]() отображает
множество
отображает
множество
![]() на
множество
на
множество
![]() .
.
Областью
определения функции
![]() называется множество допустимых
значений аргумента x.
Обозначается: D(f)
называется множество допустимых
значений аргумента x.
Обозначается: D(f)
Областью значения функции называется множество всех y, которые может принимать функция. Обозначается: E(f).
В курсе математического анализа изучают главным образом числовые функции, т.е. функции, для которых оба множества X и Y состоят из чисел.
Наглядное представление о числовой функции дает ее график.
График
функции
с областью определения D
называется множество точек плоскости
:
![]() .
.
Функция может быть задана различными способами. Наиболее употребительными являются следующие четыре способа задания функции.
Способ |
Описание |
Пример |
Аналитический |
задание функции с помощью формулы, указывающей, какие действия нужно произвести над x , чтобы получить y. Это способ наиболее часто встречается на практике. |
Формула для
задания функции может быть задана
явно или неявно. Функция задана явно,
если она задана формулой
.
Например,
|
Графический |
задание функции с помощью графика |
ЭКГ у пациента или показания осциллографа |
Табличный |
задание функции в виде таблицы, содержащей значения аргумента x и соответствующие значения функции f(x) |
Таблица выигрышей в лотерею или таблица значений функции Пуассона и т.д. |
Словесный |
с помощью естественного языка |
Игрек равно целая часть от икс. |
Основные свойства и виды функций
Перечислим основные свойства функций.
1. Четность,
нечетность.
Функция
называется четной,
если для любых значений x
из области определения X
значение
![]() также принадлежит X
и выполнено
также принадлежит X
и выполнено
![]() и нечетной,
если
и нечетной,
если
![]() .
В противном случае функция называется
функцией
общего вида.
.
В противном случае функция называется
функцией
общего вида.
Например,
![]() четная
функция,
четная
функция,
![]() нечетная
функция.
нечетная
функция.
2. Монотонность. Функции, возрастающие и убывающие называются монотонными функциями.
Функция
возрастающая
на (а;b),
если большему значению аргумента
соответствует большее значение функции,
т.е. для любых
![]() .
.
Функция
убывающая
на (а;b),
если большему значению аргумента
соответствует меньшее значение функции,
т.е. для любых
![]()
3. Ограниченность.
Функция
называется ограниченной
на промежутке X,
если существует
число М>0,
что
![]()
Например, функция
![]() - ограничена на всей числовой оси (М=1).
- ограничена на всей числовой оси (М=1).
Функции могут быть
ограничены
сверху,
когда при тех же условиях выполнено
![]() ограничены снизу, если
выполнено
ограничены снизу, если
выполнено
![]()
4. Периодичность.
Функция
называется периодической
с периодом
![]() если для любых значений x
из области определения X,
значение
если для любых значений x
из области определения X,
значение
![]() также принадлежит X
и выполнено
также принадлежит X
и выполнено
![]() Например, функция
Например, функция
![]() является периодической с периодом
является периодической с периодом
![]()
5. Обратная
функция.
Пусть
-
функция, с областью определения X
и областью
значений Y.
Дополнительно
предположим, что разным значениям
х соответствуют
разные значения
y.
Тогда, для каждого
![]() существует единственное значение
существует единственное значение
![]() такое, что
такое, что
![]() Поставим в соответствие каждому
единственное значение
Поставим в соответствие каждому
единственное значение
![]() Функцию
Функцию
![]() определенную на множестве Y
с областью
значений X
называют
обратной
к функции
и обозначается
определенную на множестве Y
с областью
значений X
называют
обратной
к функции
и обозначается
![]()
На практике,
аргумент в обратной функции обозначается
через х,
а значение функции через y.
Тогда, обратная функция запишется
![]()
Например, для
функции
![]() обратной будет
обратной будет
![]() или в обычных обозначениях
или в обычных обозначениях
![]() ;
для функции
;
для функции
![]() обратной будет функция
обратной будет функция
![]() Графики взаимно-обратных функция
симметричны относительно биссектрисы
у = х
первого и третьего координатных углов.
Графики взаимно-обратных функция
симметричны относительно биссектрисы
у = х
первого и третьего координатных углов.
Теорема 4.1. Для любой строго монотонной функции существует обратная функция.
Доказательство. Из определения обратной функции, функция имеет обратную тогда и только тогда, когда имеется взаимно однозначное соответствие между множествами X и Y.
6. Сложная
функция.
Если величина y
является функцией от u,
то есть
![]() ,
а u,
в свою очередь, функцией от x,
то есть
,
а u,
в свою очередь, функцией от x,
то есть
![]() ,
то
,
то
![]() является сложной
функцией от
x (суперпозиция
функций, композиция функций, функция
от функции). Например, две функции
является сложной
функцией от
x (суперпозиция
функций, композиция функций, функция
от функции). Например, две функции
![]() и
и
![]() определяют сложную функцию
определяют сложную функцию
![]() .
.
7. Основные элементарные функции:
Степенные функции.
Показательные функции.
Логарифмические функции.
Тригонометрические функции.
Обратные тригонометрические функции.
Функции, построенные из основных с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.