
- •Введение в предмет
- •Лекция 1.1.
- •Математика, ее история, основные элементы и методы
- •1. Предмет, задачи и содержание курса «Математика»
- •2. История развития математики, ее основные этапы
- •3. Развитие понятия числа. Комплексные числа.
- •Контрольные вопросы
- •Раздел I.
- •Тема 2.
- •1. Понятие системы линейных алгебраических уравнений
- •2. Понятие матрицы, виды матриц
- •3. Определители и их свойства. Формулы Крамера
- •1. Арифметические операции над матрицам
- •1)Сложение матриц
- •2) Вычитание матриц
- •3)Умножение матрицы на число
- •4) Произведение матриц
- •2. Понятие обратной матрицы и метод ее нахождения
- •3. Решение систем линейных алгебраических уравнений матричным методом
- •2. Метод Гаусса решения слау
- •Контрольные вопросы
- •Тема 3.
- •Элементы векторной алгебры и аналитической геометрии
- •Лекция 3.1.
- •Вектора
- •1. Вектор. Линейные операции над геометрическими векторами
- •Проекция вектора на ось. Разложение вектора по ортам координатных осей
- •Действия над векторами в координатной форме
- •Лекция 3.2. Нелинейные операции над векторами. Линейная независимость векторов и базис пространства.
- •2. Линейная зависимость и линейная независимость векторов Лекция 3.3 Аналитическая геометрия на плоскости и а пространстве
- •1. Метод координат на плоскости
- •2. Виды уравнений прямой на плоскости
- •3. Условия параллельности и перпендикулярности прямых на плоскости
- •4. Прямая и плоскость в пространстве
- •Контрольные вопросы
- •Раздел II.
- •Тема 4.
- •1. Множества и операции над ними
- •2. Понятие функции, ее свойства
- •3. Понятие числовой последовательности
- •Лекция 4.2. Предел функции, основные свойства
- •1. Предел числовой последовательности и его свойства
- •2. Понятие предела функции
- •3. Основные теоремы о пределах
- •Лекция 4.3. Бесконечно малые и бесконечно большие функции, их свойства
- •1. Понятие бесконечно малых и бесконечно больших функции, их свойства
- •2. Эквивалентные бесконечно малые функции
- •Раскрытие неопределенностей
- •Лекция 4.4. Замечательные пределы. Непрерывность функций
- •1. Первый замечательный предел
- •Второй замечательный предел
- •Непрерывные функции и их свойства
- •Контрольные вопросы
- •Тема 5.
- •Задачи, приводящие к понятию производной
- •Понятие смысл производной
- •Лекция 5.2. Понятие дифференциала функции и его применение в приближенных вычислениях
- •1. Понятие дифференциала функции, его свойства и геометрический смысл
- •2. Применение дифференциала в приближенных вычислениях
- •Лекция 6.3 Приложение понятия производной
- •Основные теоремы о дифференцируемых функциях
- •Применение производных для вычисления пределов функций (правило Лопиталя)
- •Задания для самостоятельной работы
- •Возрастание и убывание функций. Экстремумы функции
- •Лекция 5.4. Общее исследование функций с помощью производной
- •Контрольные вопросы
- •Тема 6.
- •Дифференциальное исчисление функции нескольких переменных
- •Лекция 6.1.
- •Фнп. Частные производные
- •1.Понятие функции двух и нескольких переменных
- •Лекция 6.2. Приложения понятия частных производных
- •Производная по направлению
- •2. Градиент функции и его применение
- •1. Определение первообразной и неопределенного интеграла
- •2. Непосредственное интегрирование
- •3. Основные методы интегрирования
- •Лекция 7.2. Определенный интеграл и его вычисление
- •Задача о площади криволинейной трапеции
- •Понятие определенного интеграла и его свойства
- •3.Формула Ньютона-Лейбница и основные методы нахождения определенного интеграла
- •Лекция 7.3. Определенный интеграл и его вычисление
- •Понятие несобственного интеграла второго рода
- •Приложения определенного интеграла
- •Контрольные вопросы по теме
- •Тема 8.
- •Дифференциальные уравнения
- •Лекция 8.1.
- •Дифференциальные уравнения первого порядка, их виды и методы решения
- •1. Понятие дифференциального уравнения и его решения
- •2. Дифференциальное уравнение первого порядка. Задача Коши
- •3. Основные виды дифференциальных уравнений первого порядка
- •Лекция 8.2. Дифференциальные уравнения высших порядков
- •1. Дифференциальные уравнения второго порядка, допускающие понижения порядка
- •2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные дифференциальные уравнения (лоду) второго порядка с постоянными коэффициентами
- •1. Понятие числового ряда, его сходимость и сумма
- •1.2. Примеры числовых рядов.
- •Лекция 9.2. Степенной ряд и его область сходимости.
- •2. Степенной ряд, вид его области сходимости
- •Контрольные вопросы
3. Понятие числовой последовательности
Рассмотрим особый вид функции- числовую последовательность.
Пусть задана
некоторая функция
,
аргумент которой будет натуральным
числом (![]() , т.е.
, т.е.
если
,
то
![]()
если
![]() ,
то
,
то
![]()
…..
если
![]() ,
то
,
то
![]()
Значения этой
функции
![]() будут
определять бесконечный ряд чисел,
называемый последовательностью.
будут
определять бесконечный ряд чисел,
называемый последовательностью.
Бесконечной числовой последовательностью называется бесконечный ряд, занумерованный числами натурального ряда в порядке возрастания или убывания номеров. Иначе говоря, числовая последовательность это функция, заданная на множестве натуральных чисел.
Числовая последовательность это функция натурального аргумента.
На практике,
числовую последовательность записывают
![]() .
Числа
называются членами
последовательности,
а
.
Числа
называются членами
последовательности,
а
![]() общий
член или n-й
член числовой последовательности.
По общему члену
общий
член или n-й
член числовой последовательности.
По общему члену
![]() всегда
можно найти любой член последовательности,
подставив вместо n
нужное число.
всегда
можно найти любой член последовательности,
подставив вместо n
нужное число.
Последовательность
считается
заданной, если задан закон, по которому
она образуется, т.е. правило нахождения
общего члена
![]()
Пример:
1)
![]() -
формула
общего члена;
-
формула
общего члена;
![]() -члены
числовой последовательности;
-члены
числовой последовательности;
2)
![]() формула общего члена;
формула общего члена;
![]() -члены
числовой последовательности.
-члены
числовой последовательности.
Так как последовательность- это частный вид функции, то, как и функции, последовательности могут быть ограниченными и неограниченными, возрастающими и убывающими. Например,
1)
![]() ограниченная,
убывающая.
ограниченная,
убывающая.
2)
![]() ограниченная,
не монотонная.
ограниченная,
не монотонная.
3)
![]() неограниченна,
не монотонна.
неограниченна,
не монотонна.
Лекция 4.2. Предел функции, основные свойства
Время -2 а.ч.
План:
1. Предел числовой последовательности и его свойства
2. Понятие предела функции
3. Основные теоремы о пределах
В математическом анализе широко используется представление некоторых словесных выражений в виде символов которые называются кванторами.
Основными кванторами являются:
![]() -
знак логического следования (одно
следует из другого)
-
знак логического следования (одно
следует из другого)
![]() -
знак равносильности
-
знак равносильности
- знак принадлежности
![]() -
знак непринадлежности
-
знак непринадлежности
![]() -
квантор существования (соответствует
словам «имеется», «найдется»)
-
квантор существования (соответствует
словам «имеется», «найдется»)
![]() -
квантор общности (соответствует словам
«для любого», «для всех»)
-
квантор общности (соответствует словам
«для любого», «для всех»)
![]() -множество
элементов
x, удовлетворяющих
условию P(x)
-множество
элементов
x, удовлетворяющих
условию P(x)
1. Предел числовой последовательности и его свойства
Пример. Пусть в тире тренировались два стрелка: хороший - назовем его "Снайпер", и плохой - "Мазила".
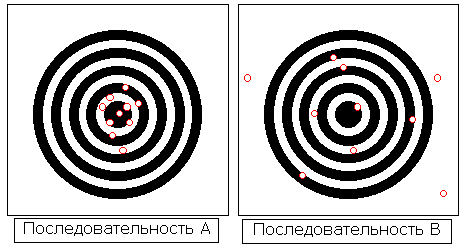
Если внимательно посмотреть на результаты этой тренировки, то нетрудно заметить, что последовательность выстрелов "Снайпера" (последовательность А) вся находится не только внутри мишени, но и, более того, как бы "стремится" к центру мишени ("яблочко"). А вот у "Мазилы" дела плохи (последовательность В)- выстрелы разбросаны по всей мишени в абсолютном беспорядке, несколько даже оказались в "молоке". Математики в этом случае говорят, что последовательность А сходится (к центру, к "10"), а последовательность В - расходится. Число, к которому сходится последовательность А (число 10) называют пределом сходящейся последовательности.
Точка сгущения- точка, к которой стягиваются члены числовой последовательности. В любой окрестности точки сгущения окажутся бесконечное множество членов числовой последовательности. Существуют последовательности, которые имеют единственную точку сгущения. В этом случае ее называют пределом числовой последовательности. Математики не любят термин «точка сгущения для членов последовательности», они предпочитают использовать термин «предел последовательности».
Дадим строгие определение предела последовательности, а так же определения сходящейся и расходящейся последовательности.
Число а называется
пределом
числовой последовательности
(переменной)
,
если для любого сколь угодно малого,
наперед задуманного, положительного
числа ![]() найдется такой номер N
начиная с которого для всех членов
последовательности с номерами
найдется такой номер N
начиная с которого для всех членов
последовательности с номерами ![]() верно
неравенство
верно
неравенство
![]() .
.
Предел числовой
последовательности обозначается
![]() или
или
![]() при
при
![]() .
.
На языке кванторов определение предела имеет вид:
![]()
Числовые последовательности, имеющие конечный предел называются сходящимися. Если предел последовательности не существует или равен бесконечности, то последовательность называется расходящейся.
Смысл определения
предела числовой последовательности
состоит в том, что для достаточно больших
n
члены последовательности
сколь угодно мало отличаются от числа
а. Например,
члены
числовой последовательности
![]() имеют вид:
имеют вид:
![]() .
Пределом этой
последовательности является число
"ноль". Действительно, если изобразить
эту последовательность на числовой
оси, то мы увидим, что все члены
последовательности как бы стремятся
"слипнуться" с нулем. (рис….)
.
Пределом этой
последовательности является число
"ноль". Действительно, если изобразить
эту последовательность на числовой
оси, то мы увидим, что все члены
последовательности как бы стремятся
"слипнуться" с нулем. (рис….)
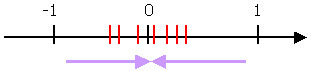 Рисунок 1…
Рисунок 1…
Исходя из
вышеизложенного, можно записать:
![]() Пример:
Дана последовательность
Пример:
Дана последовательность![]() .1)
Доказать,
что число 1 является ее пределом; 2) при
каких n
выполняется неравенство
.1)
Доказать,
что число 1 является ее пределом; 2) при
каких n
выполняется неравенство
![]()
Решение.
1) Докажем, используя определение предела.
Возьмем произвольное
![]() и покажем, что можно найти такой номер
N
начиная с которого для всех членов
последовательности с номерами
верно
неравенство
и покажем, что можно найти такой номер
N
начиная с которого для всех членов
последовательности с номерами
верно
неравенство
![]()
Преобразуем это неравенство:
![]()
Очевидно, что если
принять N
равным
ближайшему целому числу, большим величины
![]() например,
например,![]() то будет выполняться неравенство
то будет выполняться неравенство
2) В нашем случае
![]() ,
тогда
,
тогда
![]() .
Отсюда имеем, что все члены последовательности
с номерами
.
Отсюда имеем, что все члены последовательности
с номерами
![]() удовлетворяют неравенству
удовлетворяют неравенству
![]() иными словами, отличаются от своего
предела не больше, чем на 0,01.
иными словами, отличаются от своего
предела не больше, чем на 0,01.
Для лучшего понимания понятия предела последовательности полезно использовать его геометрический смысл.
Неравенство
эквивалентное неравенству
![]() ,
означает, что для любого
существует такой номер
N,
, что все члены последовательности
с номерами
расположены между
,
означает, что для любого
существует такой номер
N,
, что все члены последовательности
с номерами
расположены между![]() и
и
![]() .
.
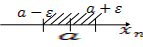
Переменная
сгущается, накапливается возле своего
предела и в интервале
![]() находится бесконечное число, а вне её,
конечное.
находится бесконечное число, а вне её,
конечное.
Замечание.
Если число а
— предел последовательности
,
то, образно выражаясь,
—
это «ловушка» для последовательности:
начиная с некоторого номера![]() эта ловушка «заглатывает»
и все
последующие члены последовательности.
Чем «тоньше» ловушка, тем дольше
«сопротивляется» последовательность,
но потом все равно «подписывает акт о
капитуляции» — попадает в выбранную
окрестность.
эта ловушка «заглатывает»
и все
последующие члены последовательности.
Чем «тоньше» ловушка, тем дольше
«сопротивляется» последовательность,
но потом все равно «подписывает акт о
капитуляции» — попадает в выбранную
окрестность.
Основные теоремы о пределах последовательности
Теорема 4.2. Сходящая последовательность имеет только единственный предел.
Доказательство:
Предположим, противное- что сходящаяся
последовательность
имеет
два различных предела
![]() и
и
![]() причем
причем
![]() стр. 63 Хамов
стр. 63 Хамов
Остальные теоремы приведем без доказательства.
Теорема 4.3. Сходящаяся последовательность всегда ограничена.
Теорема 4.4.
(о предельном
переходе в неравенстве).
Если
![]() и начиная с некоторого номера, выполняется
и начиная с некоторого номера, выполняется
![]() то и
то и
![]()
Теорема 4.5.
(о сжатой
переменной).
Если члены
трех последовательностей связаны
неравенствами
![]() и
при этом последовательности
и
и
при этом последовательности
и
![]() имеют
один и тот же предел а,
т.е.
имеют
один и тот же предел а,
т.е.
![]() ,
то и последовательность
,
то и последовательность
![]() имеет предел
а, т.е.
имеет предел
а, т.е.
![]() .
.
Теорема 4.6. (теорема Вейерштрасса о существовании предела монотонной последовательности). Любая монотонная и ограниченная последовательность имеет предел.
Итак, было рассмотрено понятие предела функции натурального аргумента- числовой последовательности. Обобщим это понятие для произвольной функции.
