1. Арифметические операции над матрицам

Над матрицами, как над числами можно производить ряд операций, причем некоторые из них аналогичны числовым операциям, а некоторые носят особый характер.

1)Сложение матриц

Операция сложения вводится только для матриц одинаковых размеров.

Суммой двух матриц одинаковой размерности и называется матрица той же размерности , такая, что ,

Таким образом, чтобы сложить две матрицы, нужно сложить их соответствующие элементы. Помните, что складывать можно только матрицы одинаковой размерности.

Пример.

А= ; B= ; А+B=

2) Вычитание матриц

Разностью двух матриц одинаковой размерности и называется матрица той же размерности , такая, что ,

Таким образом, чтобы из матрицы А вычесть матрицу В, нужно из элементов матрицы А вычесть соответствующие элементы матрицы В.

Пример.

А= , B= , А-B= .

3)Умножение матрицы на число

Произведением матрицы на число k называется матрица , такая, что ,

Таким образом, чтобы умножить матрицу на число нужно все элементы данной матрицы умножить на это число.

Пример.

А= , то 3А= .

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Пример.

А= , то 2А= .

Замечание. Разность матриц можно определить так: .

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

1) (коммутативность);

2) = A + B + C (ассоциативность);

3) ;

4) ; .

5) (дистрибутивность относительно сложения чисел);

6) (дистрибутивность относительно сложения матриц);

7) (ассоциативность), где ; A, B, C – матрицы.

4) Произведение матриц

Произведением матриц и называется матрица, , у которой элемент равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В, то есть ,

Замечание. При умножении матриц количество столбцов первой матрицы А обязательно должно совпадать с количеством строк второй матрицы В.

Пример. Пусть 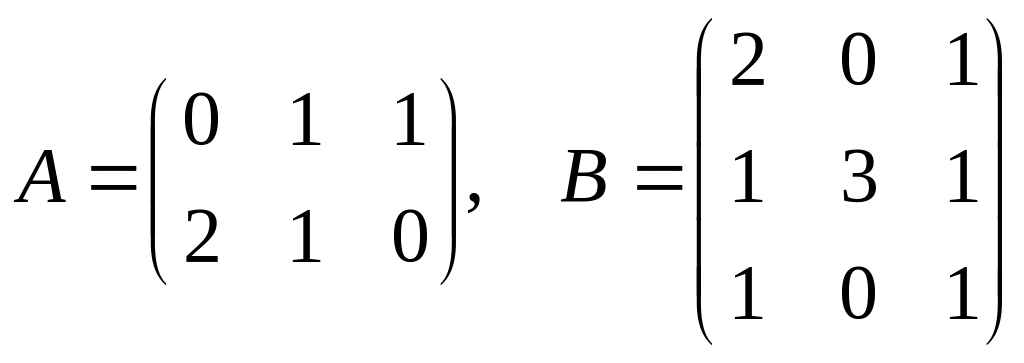. Найти

Решение. Здесь и , значит . Вычислим элементы матрицы С.

Тогда,

Свойства умножения матриц:

1) (ассоциативность);

2) ; ;

3) ; (дистрибутивность);

4) Для произвольных матриц - отсутствие коммутативности.

Например, А= и В= . Тогда , а , т.е. .

Однако существует матрица, для которой переместительный закон будет выполняться. Если матрица А- квадратная матрица порядка n и Е-единичная матрица того же порядка, то . Кроме единичной существуют и другие матрицы, для которых переместительный закон будет выполняться. Их называют перестановочными.

Например, перестановочными матрицами будут матрицы А= и В= . Для них .

Заметим, что если произведение матриц равно нулю, то совсем необязательно, чтобы какой-то из сомножителей был бы нулевой матрицей.

Например,

2. Понятие обратной матрицы и метод ее нахождения

Для каждого ненулевого число существует обратное число, такое что произведение этих чисел равно единице. Для квадратных матриц тоже существует такое понятие как обратная матрица.

Матрица называется обратной по отношению к матрице , если при умножении этой матрицы на данную как справа, так и слева получиться единичная матрица, т.е.

.

Матрица называется невырожденной, если ее определитель не равен нулю. В противном случае матрица называется вырожденной.

Матрица называется дополнительной к матрице , если ее элементы есть алгебраические дополнения соответствующих элементов матрицы .

Теорема 2.2. Любая невырожденная матрица имеет обратную.

Доказательство. Докажем теорему для матрицы третьего порядка.

Пусть дана матрица третьего порядка . По условию

Рассмотрим дополнительную матрицу и ее транспонированную матрицу .

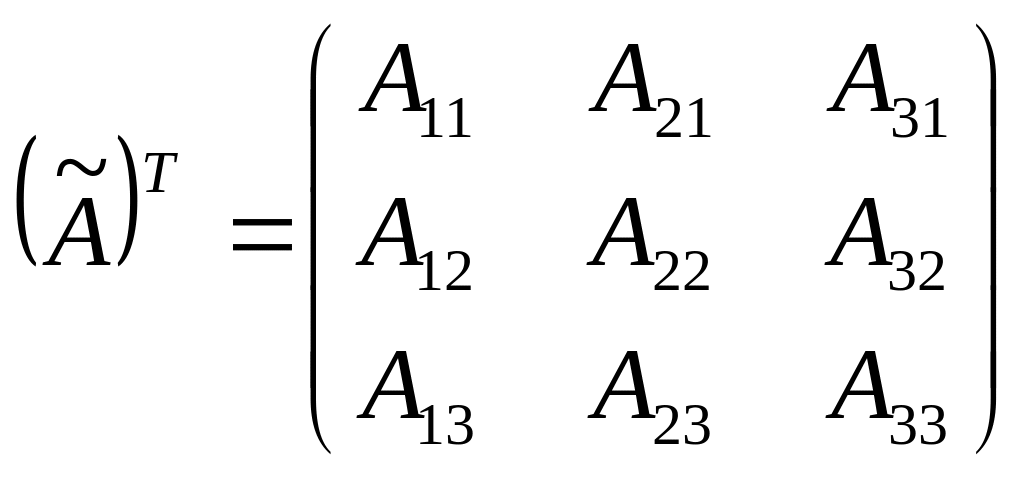Найдем произведение матриц

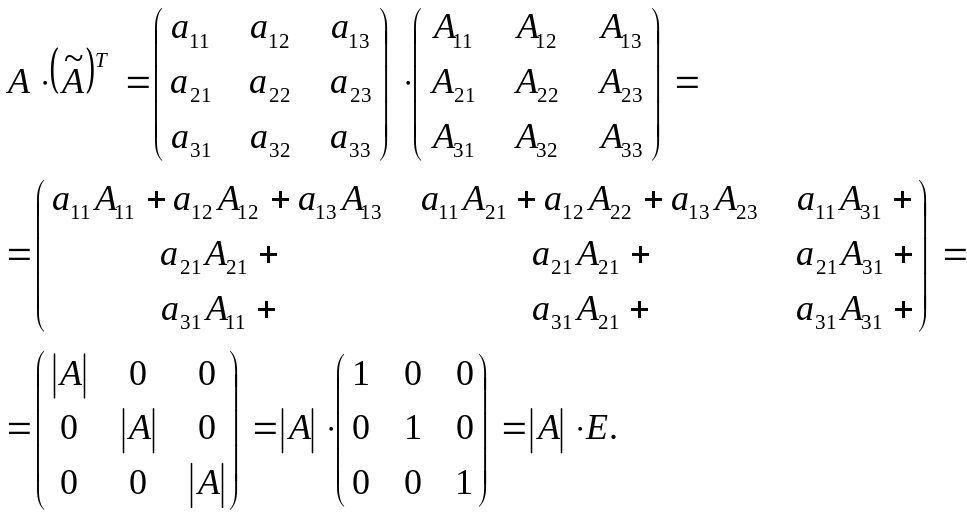
Использовали 8 свойство определителей, теорема 2.1. и правило умножения матрицы на число.

Аналогично можно получить равенство

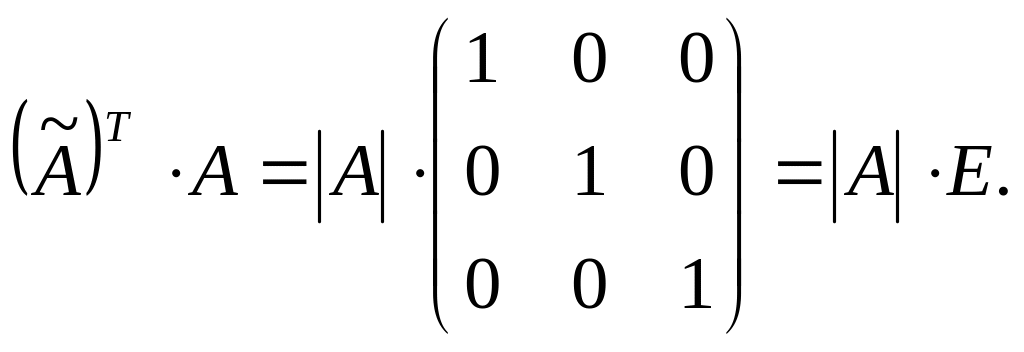
Определим обратную матрицу по формуле

(2.5)

и проверим, является ли она обратной к матрице А.

Из определения, найдем произведения

Таким образом, формула (2.5) обратной матрицы определена верно.

Теорема доказана.

Замечание. Обратная матрица всегда единственна.

Правило нахождения обратной матрицы.

1) найти определитель матрицы ;

2) найти дополнительную матрицу ;

3) транспонировать дополнительную матрицу, т.е. найти ;

4) разделить каждый элемент транспонированной дополнительной матрицы на значение определителя исходной матрицы.

Пример 2.4. Найти обратную матрицу к матрице

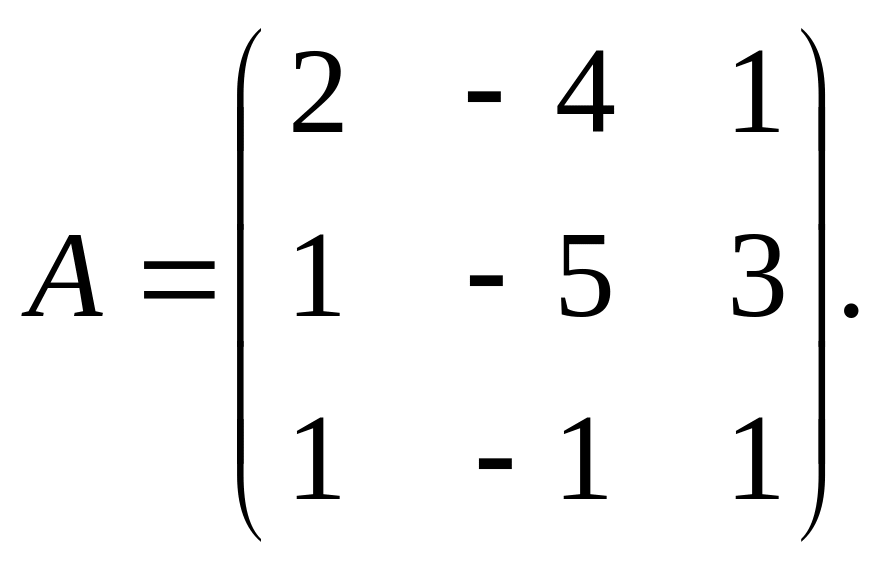
Решение.

1) Найдем определитель матрицы :

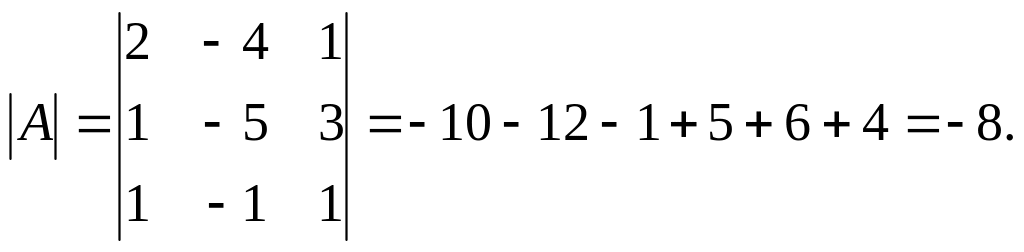
2) найдем дополнительную матрицу .

3) транспонируем дополнительную матрицу

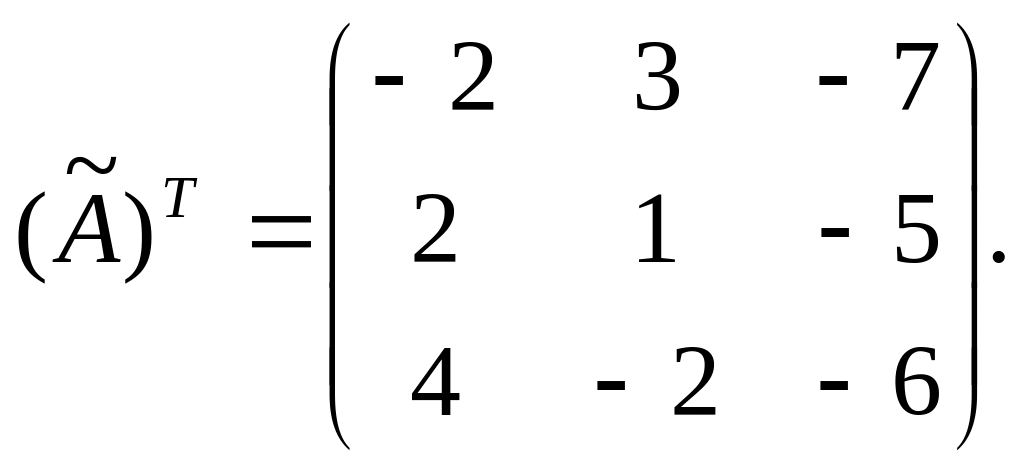
4) найдем обратную матрицу, разделив каждый элемент транспонированной дополнительной матрицы на значение определителя исходной матрицы:

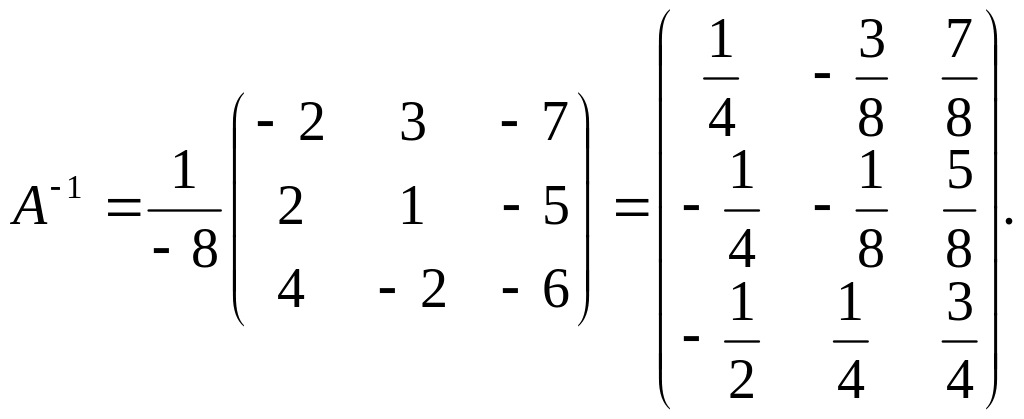
Проверим, что обратная матрица найдена верно. Для этого найдем произведение обратной матрицы на исходную матрицу .

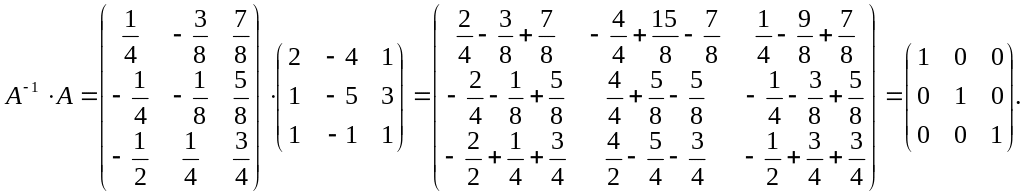Итак, обратная матрица найдена верно.