Линейные однородные дифференциальные уравнения (лоду) второго порядка с постоянными коэффициентами

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами –это уравнение вида

,

где p и q – действительные числа.

Будем искать решение в виде , где k-const.

Очевидно, что . Подставим эти выражения в уравнение:

def 9. Уравнение называется характеристическим уравнением дифференциального уравнения .

При решении возможны три случая:



1.

2.

3.

Контрольные вопросы

Тема 9

Числовые и функциональные ряды.

Лекция 9.1.

Числовой ряд и его сходимость.

Время -2 а.ч.

План:

1. Понятие числового ряда, его сходимость и сумма.

2. Необходимый признак сходимости числового ряда.

3. Достаточные признаки сходимости рядов с положительными членами.

4. Знакочередующиеся ряды, их сходимость по признаку Лейбница.

5. Знакопеременные ряды. Абсолютная и условная сходимость.

При решении практических задач как в математике, так и в ее приложениях, иногда приходится рассматривать суммы, составленные из бесконечного числа слагаемых. Сумма бесконечного числа слагаемых называется рядом, а задача нахождения самой суммы решается в теории рядов.

В курсе математики средней школы уже встречались с некоторыми числовыми рядами- с суммами арифметической и геометрической прогрессий. Это одни из самых первых рядов, которые появились в математике.

С развитием математического анализа начинают появляться много новых рядов. При этом постепенно происходит формирование двух классов рядов: числовые и функциональные ряды. В числовых рядах слагаемыми являются числа, в функциональных- функции. Среди всех числовых рядов принято выделять ряды с положительными членами, знакопеременные и знакочередующиеся ряды. Одним из основных видов функционального ряда является степенной ряд. Ряды представляют собой простой и совершенный инструмент математического анализа для приближенного вычисления функций, интегралов и решений дифференциальных уравнений.

Теория рядов (ряды возникли в XVIII в.) создавалась в тесной связи с теорией приближенного представления функций в виде многочленов. Впервые это сделал И. Ньютон (1642 – 1727) в 1676г. В его письме к секретарю Лондонского Королевского Общества появилась формула:

,

которую мы знаем как формулу бинома Ньютона. Здесь мы видим функцию , представленную в виде многочлена. Но если число m не является натуральным, в правой части равенства получается не полином, а бесконечная сумма слагаемых, то есть ряд.

1. Понятие числового ряда, его сходимость и сумма

Пусть дана бесконечная числовая последовательность

Выражение вида

называется числовым рядом.

элементы или члены ряда; n-ый или общий член ряда.

Иногда нумерацию членов ряда начинают не с 1, а с 0 (это особенно удобно в степенных рядах).

Если члены ряда:

• числа, то ряд называется числовым;

• числа одного знака, то ряд называется знакопостоянным;

• числа разных знаков, то ряд называется знакопеременным;

• положительные числа, то ряд называется знакоположительным;

• числа, знаки которых строго чередуются, то ряд называется знакочередующимся;

• функции, то ряд называется функциональным;

• степени x, то ряд называется степенным;

• тригонометрические функции, то ряд называется тригонометрическим.

Суммы

…………..

,

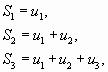
составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм .

Если при бесконечном возрастании номера n частичная сумма ряда стремится к пределу , то ряд называется сходящимся, а число - суммой сходящегося ряда, т.е.

и .

Эта запись равносильна записи

.

Если частичная сумма ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к или ), то такой ряд называется расходящимся.

Если ряд сходящийся, то значение при достаточно большом n является приближенным выражением суммы ряда S.

Разность называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. , и наоборот, если остаток стремится к нулю, то ряд сходится.