Лекция 4.4. Замечательные пределы. Непрерывность функций
Время -2 а.ч.
План:
1. Первый замечательный предел.
2. Второй замечательный предел
3. Непрерывные функции и их свойства
В математике существуют пределы, которые имеют большое прикладное и теоретическое значение. Их называют замечательными пределами. Первый из них связан с тригонометрическими функциями, а второй с показательными и логарифмическими функциями.
1. Первый замечательный предел
Первым замечательным пределом называется предел следующего вида:
(4.7)
или, иначе, предел отношения синуса к его аргументу равен единице.
Предел в формуле (4.7) имеет неопределенность .
Докажем справедливость этой формулы.
Доказательство.
Рассмотрим круг единичного радиуса с
центром в точке О
и обозначим радианную меру угла АОВ
через x,
причем
.
Р
ис
изменить-совместить точки А и С!!!!!!!
Из
рисунка видно, что площадь треугольника
АОВ меньше
площади сектора
АОВ, которая
в свою очередь меньше площади треугольника
АОC,
т.е
Площадь треугольника АОВ равна половине произведения сторон на синус угла между ними, т.е.
Площадь сектора АОВ для угла, выраженного в радианах, равна половине произведения квадрата радиуса на величину угла т.е.
Площадь прямоугольного треугольника АОС равна половине произведения катетов, т.е.
Отсюда, двойное
равенство примет вид:
.
Разделив все части
неравенства на величину
,
получим
или
Функции
и
являются четными, следовательно,
полученные неравенства справедливы и
для
Так как
и
,
то по теореме …. справедливо равенство
Формула доказана.
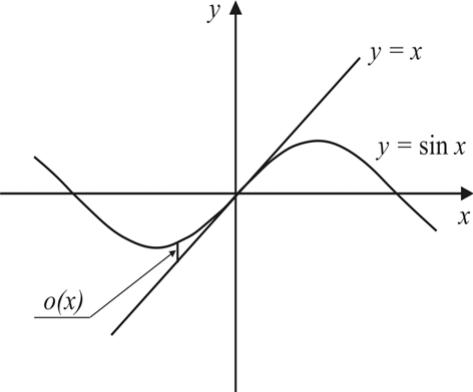
Геометрическая
иллюстрация первого замечательного
предела представлена на рис. … Видно,
что в области ноля прямая
и синусоида
практически сливаются.
Пример 4.8.
Найти предел
Решение. 1-й способ (используя 1-й замечательный предел).
К данному примеру
сразу применить формулу 4.7. нельзя,
поэтому проведем преобразования
-домножим числитель и знаменатель на
5:
2-й способ (замена эквивалентных бесконечно малых)
Так как
при
,
то заменим функции синуса на ее аргумент
получим:
Запомним формулы, которые достаточно часто используются при вычислении пределов:
Пример 4.9.
Найти предел
Решение:
Второй замечательный предел
Рассмотрим числовую последовательность, общий член которой имеет вид:
Члены рассматриваемой последовательности представлены в таблице:
|
1 |
2 |
3 |
4 |
5 |
10 |
100 |
1000 |
10000 |
|
2 |
2,25 |
2,37 |
2,44 |
2,49 |
2,59 |
2,70 |
2,717 |
2,718 |
Из таблицы видно, что члены последовательности возрастают и рост их замедляется, поэтому можно предположить, что все члены этой последовательности не превосходят числа 3. Покажем, что последовательность с общим членом возрастающая и ограниченная. Применим формулу бинома Ньютона
Подставив
и
в формулу,
получим:
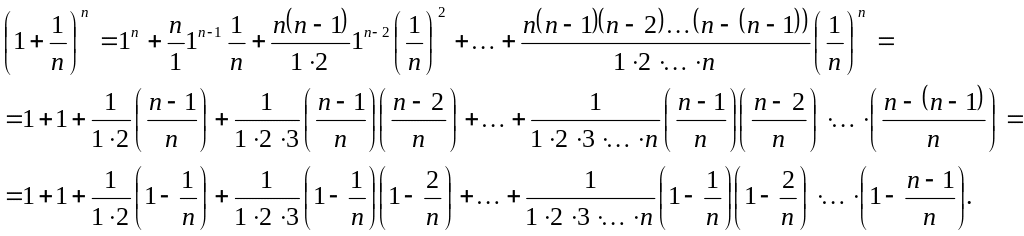Из
последнего равенства ясно, что при
увеличении n
увеличивается число положительных
слагаемых и уменьшается величина
.
Значит, величины
возрастают. Таким образом, доказано,
что рассматриваемая последовательность
возрастающая,
при этом
В последнем
представлении для
заменим каждую скобку в правой части
равенства на единицу, при этом правая
часть увеличиться, а, значит, получим
неравенство:
Последнее неравенство
усилим, заменив числа 3, 4, 5,…, стоящие в
знаменателях дробей, числом 2. Затем
применим формулу для суммы n
членов
геометрической последовательности
с первым членом
,
а знаменателем
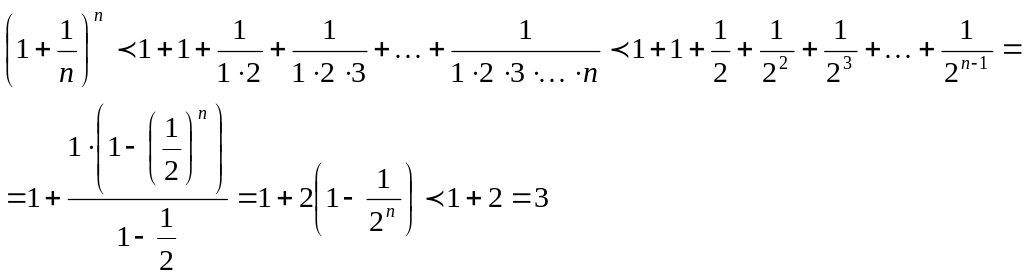
Таким образом, доказано, что рассматриваемая последовательность ограничена. По теореме 4.7??? монотонная и ограниченная последовательность имеет предел. Обозначим его через е.
Числом е
называется предел
Число е-
иррациональное и равно
Иногда число e называют числом Эйлера или числом Непера. Символ e для обозначения этого числа был введен в 1731 Л.Эйлером (1707–1783). Оно часто встречается в математике и естественных науках.
Можно показать,
что к числу е
стремиться и функция действительного
аргумента
при
.
Вторым замечательным пределом называется следующий предел
Второй замечательный
предел можно записать и в другом виде,
заменив
Тогда
причем, при
величина
Итак,
Второй замечательный
предел раскрывает неопределенность
и применяется при нахождении пределов
показательно-степенных функций.
Пример 4.9.
Найти предел
Решение. Очевидно, что имеет место неопределенность . Преобразуем данный предел к виду второго замечательного предела:
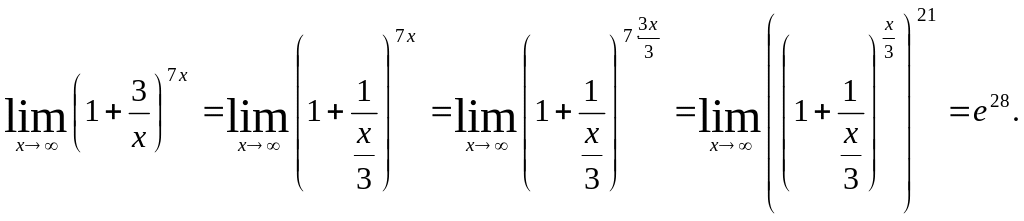
Пример 4.10.
Найти предел
Решение. Очевидно, что имеет место неопределенность . Преобразуем данный предел к виду второго замечательного предела:
