2. Непосредственное интегрирование

Из таблицы производных и определения неопределенного интеграла несложно получить таблицу интегралов:

Интегралы, содержащиеся в таблице, принято называть табличными. Одним из простейших методов интегрирования является метод непосредственного интегрирования.

Непосредственное интегрирование-метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Пример 7.1. Вычислить

Решение. Применим свойства 4 и 5 и таблицу интегралов, получаем

Необходимо обратить внимание, что ставить произвольную постоянную после вычисления каждого интеграла не следует: обычно все произвольные постоянные суммируются и результат, обозначенный одной буквой С, записывается сразу в окончательный ответ.

Пример 7.2. Вычислить

Решение. Применим свойства 4 и 5 и таблицу интегралов, получаем

Далеко не всякий интеграл можно вычислить путем непосредственного интегрирования на основании свойств интеграла и таблицы. Требуется применение некоторых методов интегрирования.

3. Основные методы интегрирования

К основным методам интегрирования относятся: метод замены переменной и метод интегрирования по частям.

Метод замены переменной (метод подстановки)

1. Метод подведения по знак дифференциала- частный случай метода замены переменной.

В основе данного метода лежит свойство инвариантности формул интегрирования (свойство 6). Рассмотрим один из табличных интегралов По свойству6 эта формула остается справедливой не только в случае, когда x –независимая переменная, но и тогда, когда вместо x стоит некоторая дифференцируемая функция. Например,

Аналогичная ситуация имеет место и для других формул:

Пример 7.3. Вычислить интеграл

Решение. Что мешает применить степенной интеграл для Понятно, что если бы под знаком дифференциала стояло выражение , а не x, то такой интеграл был бы табличным. Вопрос: возможно ли заменить на Ответ- да- по свойству дифференциала: На основании этого свойства Значит,

Пример 7.4. Вычислить интеграл

Решение. Для применения табличной формулы степенного интеграла при необходимо, чтобы под знаком дифференциала стояло выражение вместо x. По свойству дифференциала: На основании свойств дифференциала . Следовательно

При сведении интеграла к табличному часто используются следующие преобразования дифференциала -«подведение под знак дифференциала»

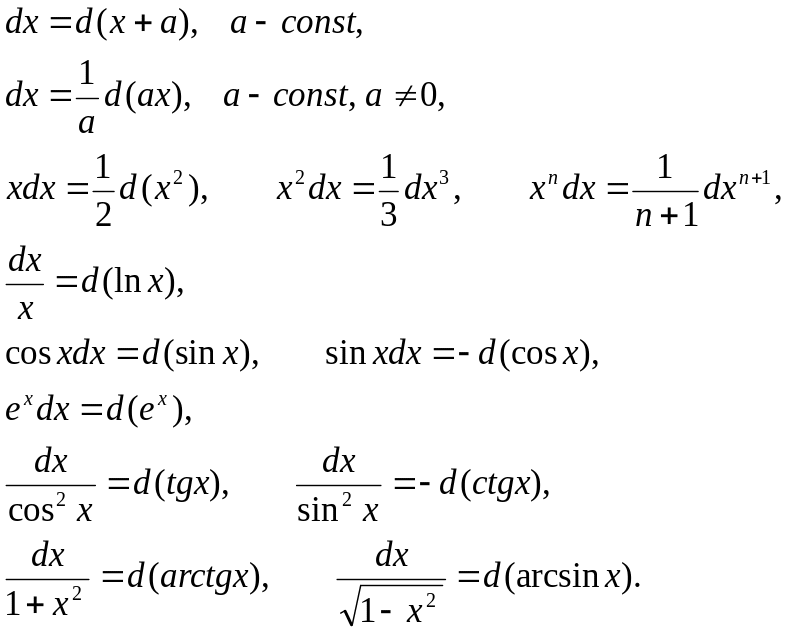
Пример 8.1. Найти интеграл

Решение. Применим…..

В рассмотренных выше примерах дифференциал изменялся на основании его свойств, т.е. вместо под знак дифференциала подводилась некоторая линейная функция вида , где и некоторые числа, причем . Обобщим это в виде теоремы.

Теорема 8.2. Пусть одна из первообразных для .

Тогда

где и некоторые числа, причем .

Итак, цель метода подведения под знак дифференциала состоит в видоизменении дифференциала, стоящего под интегралом, за счет использования свойств дифференциала.

Метод подстановки или метод замены переменной

Суть этого метода заключается в том, путем введения новой переменной интегрирования удается вести данный интеграл к новому интегралу, который сравнительной легко вычисляется непосредственно. Метод замены переменной основан на следующей теореме.

Теорема 8.3. Пусть функция определена и дифференцируема на промежутке . Тогда если первообразная для на , то выполняется равенство

Даная теорема называется формулой замены переменной в неопределенном интеграле. Удачная замена переменной позволяет упростить исходный интеграл и свести его к табличному.

Замечание 1. В практике интегрирования применяются подстановки вида , т.е. новая переменная интегрирования вводится как некоторая функция переменной х.

Замечание 2. При нахождении интеграла методом замены переменной необходимо в полученном после интегрирования результате обязательно вернуться к старой переменной.

Пример 8.3. …….

Пример 8.4….

Полезно запомнить следующие подстановки:

Метод интегрирования по частям

Пусть функции и имеют непрерывные производные на промежутке

Найдем дифференциал произведения этих функций:

Поэтому, получим или

Проинтегрируем обе части последнего равенства, получим

,

по свойству неопределенного интеграла ?номер

Эта формула называется формулой интегрирования по частям и составляет основу метода интегрирования по частям.

Суть данного метода состоит в том в том, что при нахождении интеграла подынтегральное выражение представляют в виде произведения множителей и , при этом обязательно входит в . Затем находят интегралы и

Пример 8.5……

При вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множители и . Советую запомнить следующее:

Рассмотрим интеграл вида

1. Пусть многочлен, а одна из следующих функций: тогда рекомендуют положить .

Пример 8.6…..

2. Пусть многочлен, а одна из следующих функций: тогда рекомендуют положить .

Пример 8.7…..

3. Пусть , а одна из следующих функций: тогда возможно любое разбиение, при этом формула интегрирования по частям будет применяться дважды.

Пример 8.8…..