2. Понятие матрицы, виды матриц
Матрицей
размера
называется прямоугольная таблица,
содержащая из m
строк и n
столбцов
.
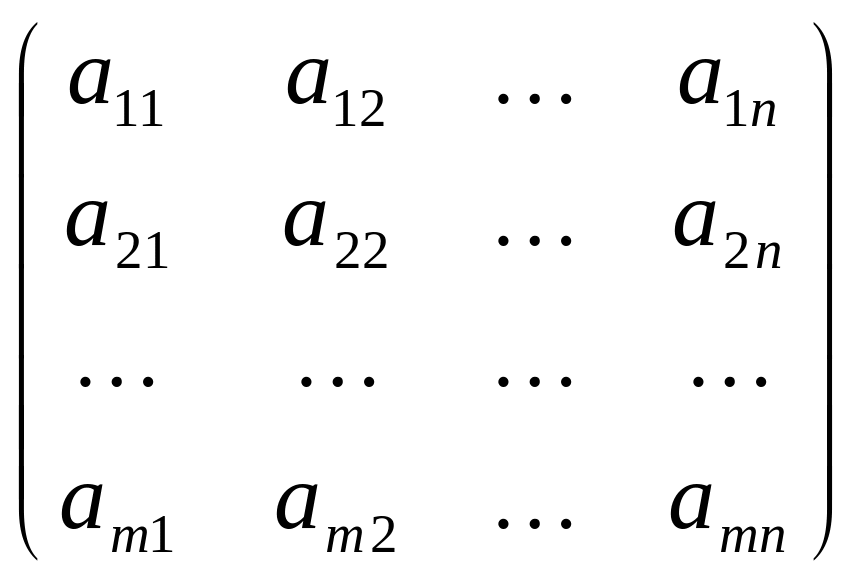Горизонтальные
ряды матрицы называют строками,
вертикальные- столбцами.
Элементы
матрицы обозначают буквами с двумя
индексами:
,
i
– номер строки, j
– номер столбца.
В общем случае, элементами матрицы могут быть различные математические объекты- числа, функции, многочлены и т.д. Однако, в нашем курсе будем рассматривать только числовые матрицы, т.е. матрицы у которых элементами являются числа.
Матрицы обозначаются большими буквами латинского алфавита, например, A;B;C…, элементы матрицы записываются в круглых скобках.
Например,
-
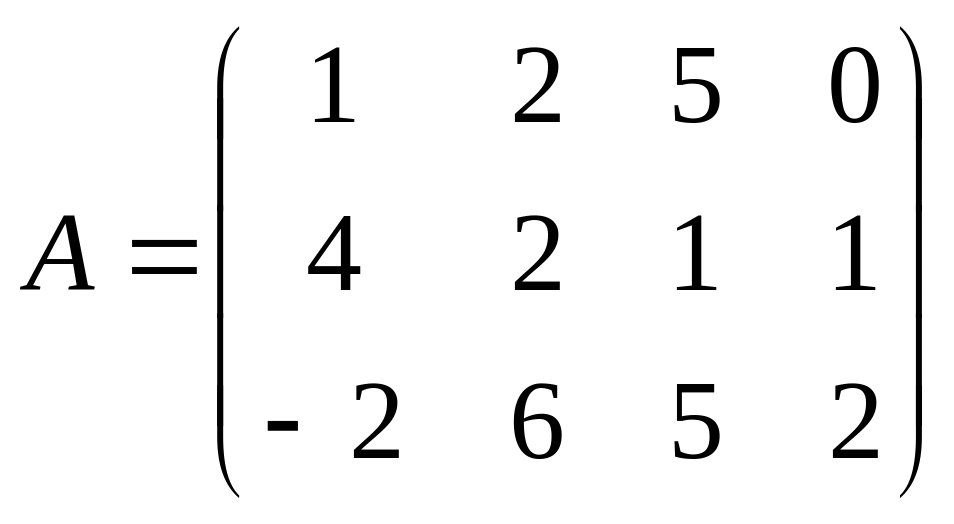матрица А
размера
Матрица называется квадратной, если число строк равно числу столбцов, т.е. m=n. Число строк (число столбцов) называется порядком матрицы.
Например,
–
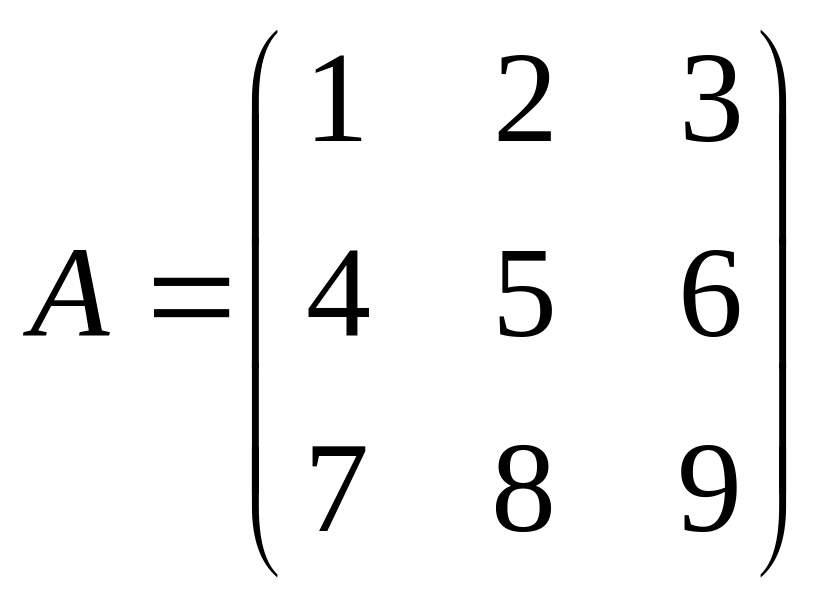квадратная матрица третьего порядка.
Диагональ квадратной
матрицы, идущая от левого верхнего к
правому нижнему углу, то есть составленная
из элементов
называется главной
диагональю матрицы.
Диагональ, идущая от правого верхнего
к левому нижнему углу, называется
побочная
диагональ матрицы.
Матрицы
и
называются
равными,
если равны все соответствующие элементы
этих матриц, т.е.
,
Матрица, состоящая из одной строки или одного столбца, называется соответственно матрицей-строкой или матрицей-столбцом.
– матрица-строка
;
– матрица-столбец
.
Матрица, все элементы которой равны нулю, называется нулевой.
Квадратная матрица, у которой не равны нулю лишь элементы главной диагонали, называется диагональной.
Например,
.
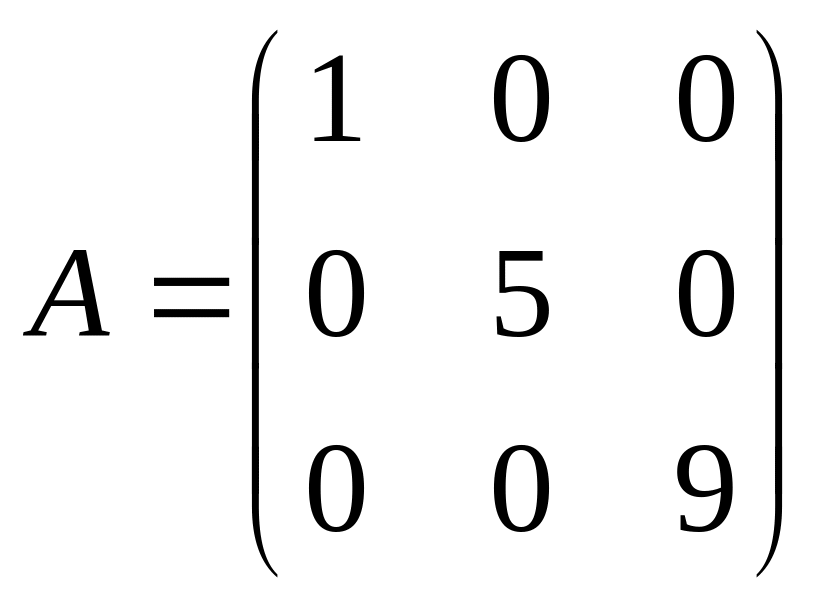Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной.
Квадратная матрица называется треугольной, если все элементы, стоящие выше или ниже главной диагонали, равны нулю.
Матрица, полученная
из данной заменой каждой ее строки
столбцом с тем же номером, называется
матрицей, транспонированной
к данной. Обозначается:
.
3. Определители и их свойства. Формулы Крамера
Каждой квадратной матрице можно поставить в соответствие некоторое число, вычисляемое по определенному правилу и называемое определителем. Необходимость введения понятия определитель тесно связано с решением СЛАУ.
Определитель
матрицы будем обозначать
или
или detA.
Определителем
(или
детерминантом) матрицы первого порядка
называется число
.
Например, для
имеем
.
Определителем
(или
детерминантом) матрицы второго порядка
называется число, определяемое по
формуле:
.
Например, если
,
то
.
Определителем
(или
детерминантом) матрицы третьего порядка
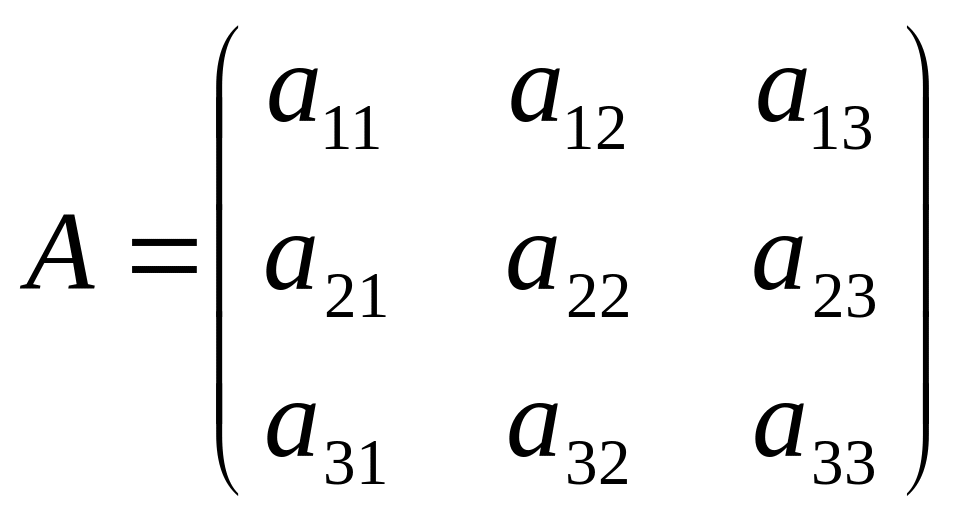называется число, определяемое по
формуле:
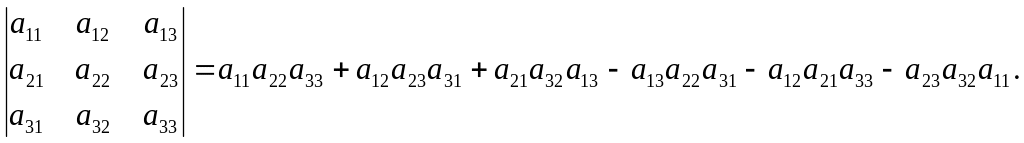
Это число представляет собой сумму шести произведений, при этом у первых трех произведений знак плюс, а у последних- знак минус. Эту формулу легко запомнить, используя схему, называемую правилом треугольника или правилом Саррюса:
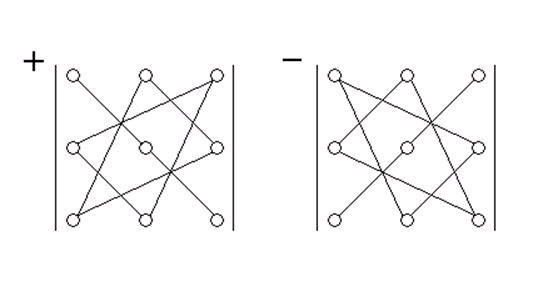
Словами можно записать: со знаком « плюс» надо взять произведение элементов, стоящих на главной диагонали, и произведение элементов, соединенных вершинами треугольников, у которых основание параллельно главной диагонали. Со знаком «минус» берутся аналогичные произведения, только относительно побочной диагонали.
Например, Дана матица третьего порядка
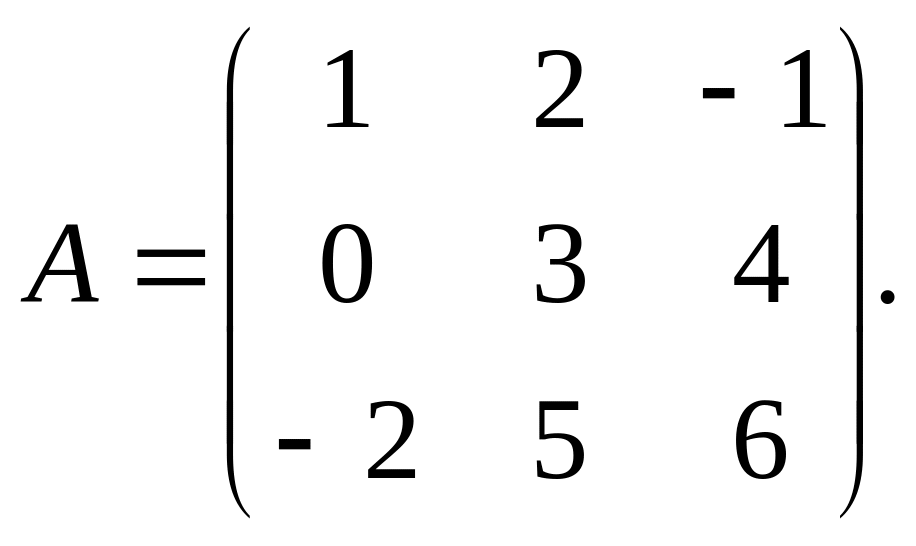Найти ее определитель.
Решение. Согласно определению получаем
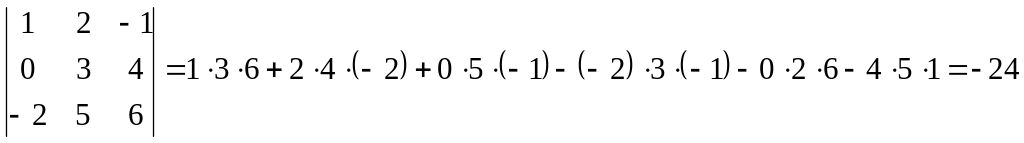
Определение определителя матрицы n-го порядка давать не будем, а лишь покажем метод его нахождения.
Введем новые вспомогательные понятия.
Пусть дана квадратная матрица n-го порядка
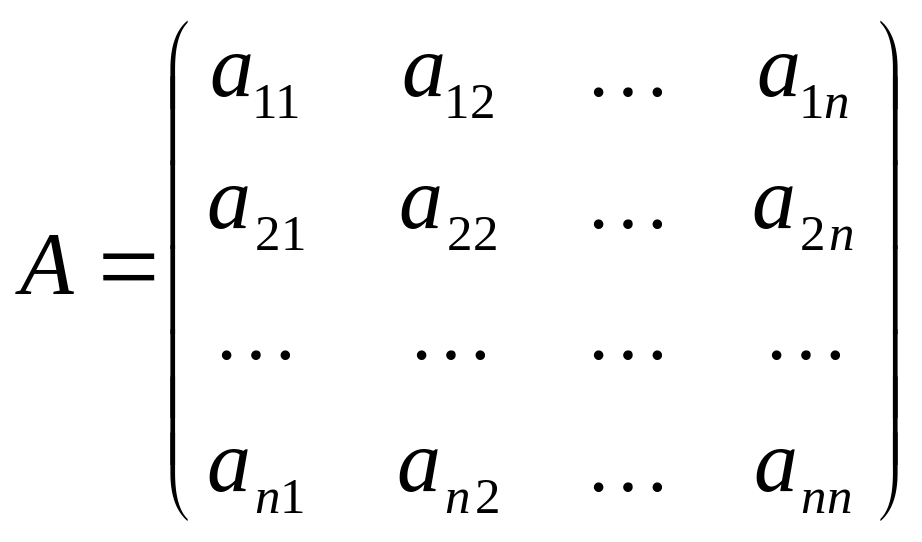и соответствующий
ей определитель
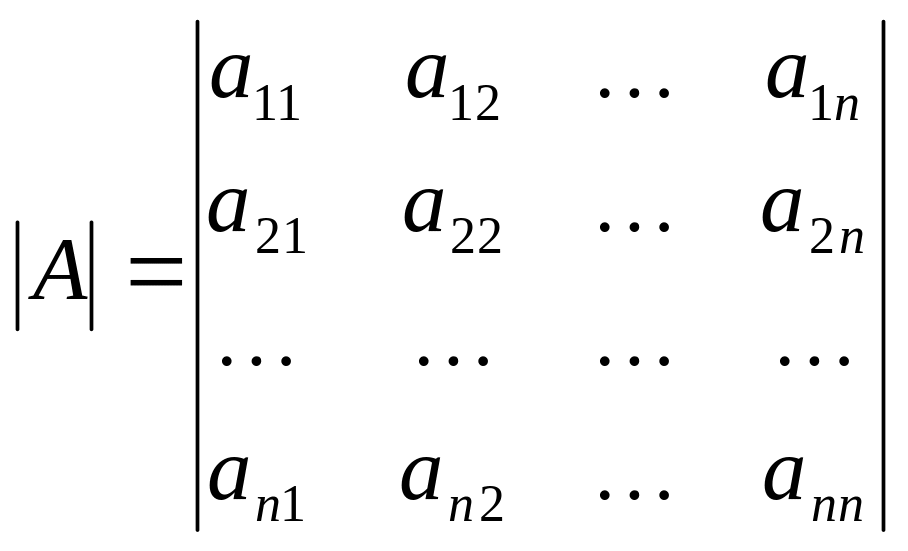
Минором
элемента
матрицы
А
называется определитель, полученный
из данного определителя вычеркиванием
i-й
строки и j-го
столбца, те той строки и того столбца,
на пересечении которого расположен
этот элемент.
Алгебраическим
дополнением
элемента
матрицы А
называется его минор, взятый со знаком
то есть
.
Алгебраическое дополнение либо совпадает со своим минором, когда сумма номеров строки и столбца- четное число, либо отличается от него знаком, когда сумма номеров строки и столбца- нечетное число.
Пример.
Дана матрица
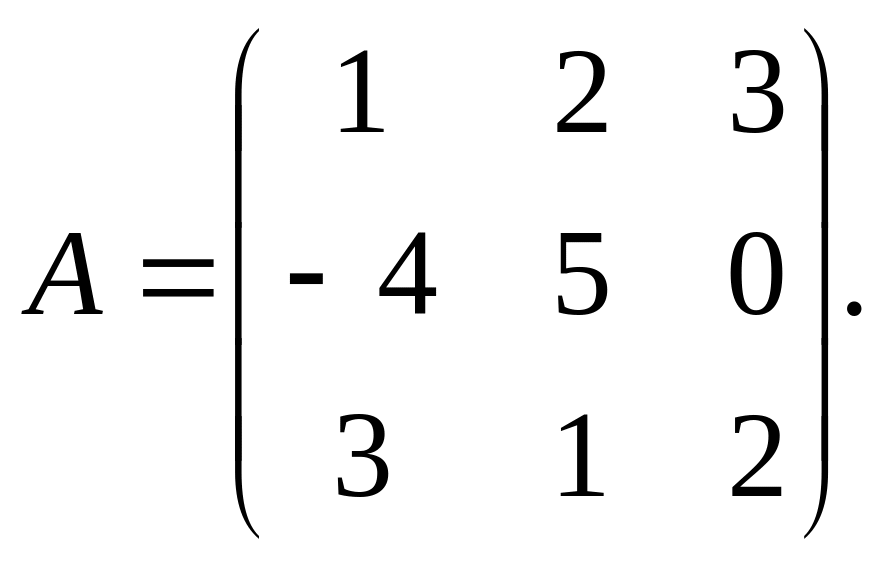Найти
Решение.
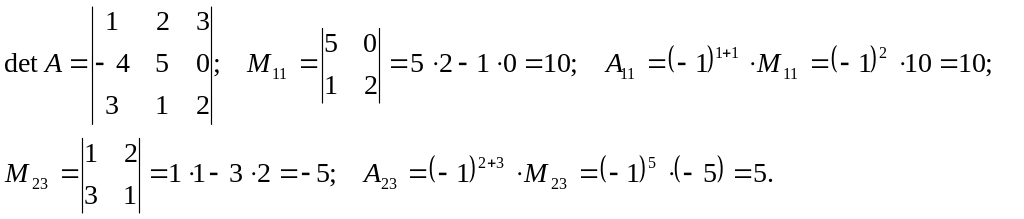
Теорема 2.1. (теорема разложения). Определитель n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т.е.
для любого
или
для любого
Доказательство. Рассмотрим теорему для определителей третьего порядка (доказательство в общем случае достаточно сложное). Найдем определитель по правилу треугольника, проведем группировку слагаемых специальным образом и разложим определитель по элементам первой строки:
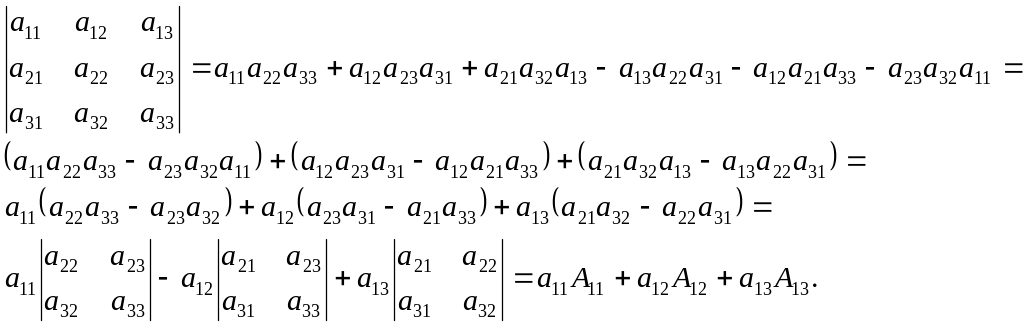
Нетрудно понять, что с помощью формул разложения определителя по строкам (столбцам) любой определитель n-го порядка можно свести к сумме определителей (n-1) порядка и т.д., пока не дойдем до определителей 3-го или 2-го порядков, вычисление которых не вызывает трудности.
Пример. Вычислить
определитель
а) разложением по элементам второго
столбца: б) разложением по элементам
первой строки.
Решение. а)
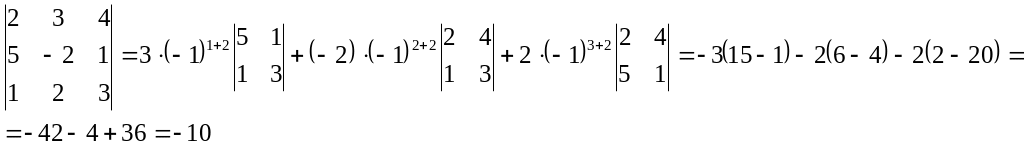
б)
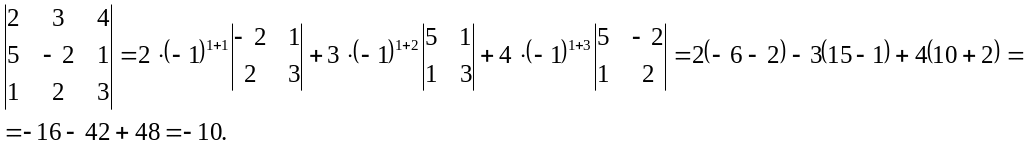
Свойства определителей
Приведем основные свойства определителей без доказательства, при этом строки и столбцы будем просто называть рядами определителя.
1. «Равноправность строк и столбцов». Величина определителя не изменится, если строки определителя заменить столбцами, а столбцы – соответствующими строками.
2. Общий множитель элементов какого-либо ряда можно вынести за знак определителя.
3. Определитель, имеющий два одинаковых ряда, равен нулю.
4. Если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
5. При перестановке двух параллельных рядов определитель меняет знак на противоположный.
6. Если один из рядов определителя состоит из нулей, то определитель равен нулю.
7. «Элементарные преобразования определителя». Значение определителя не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Формулы Крамера для решения СЛАУ
Рассмотрим СЛАУ вида:
(1.2)
Обозначим
-матрица
системы,
-
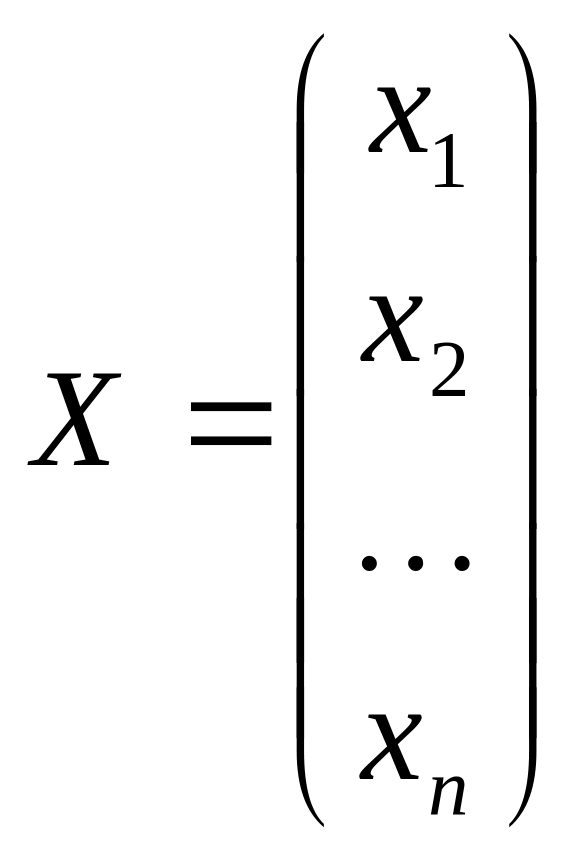матрица-столбец неизвестных,
-
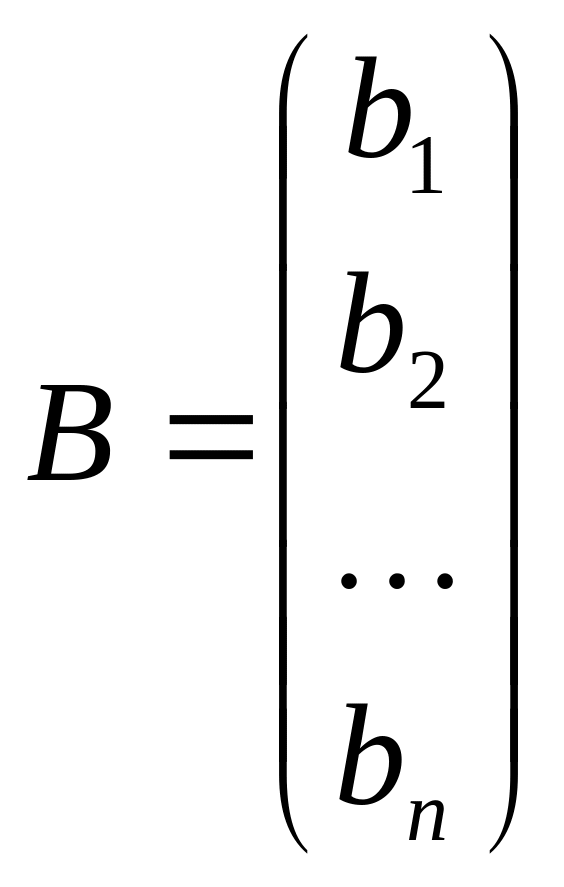матрица-столбец свободных членов.
Теорема 1.3. (правило Крамера). Если определитель матрицы системы (1.2) отличен от нуля, то данная СЛАУ имеет единственное решение, и оно находится по формулам:
,
(1.3)
где
определитель
матрицы системы,
определитель
матрицы, полученный из матрицы системы
заменой i-го
столбца столбцом свободных членов.
Доказательство для СЛАУ двух уравнений с двумя неизвестными.
Пусть дана СЛАУ
вида:
Найдем ее решение
методом исключения неизвестных (исключим
),
для этого умножим первое уравнение на
,
втрое уравнение на
Сложим почленно
полученные уравнения, вынесем за скобку
и получим:
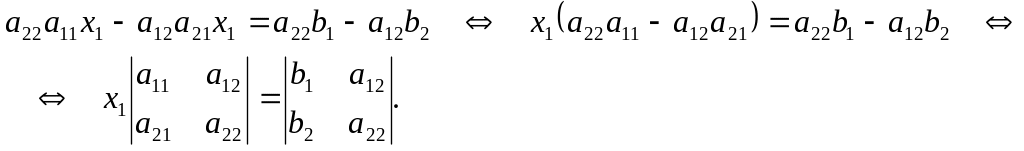
Если
,
то
.
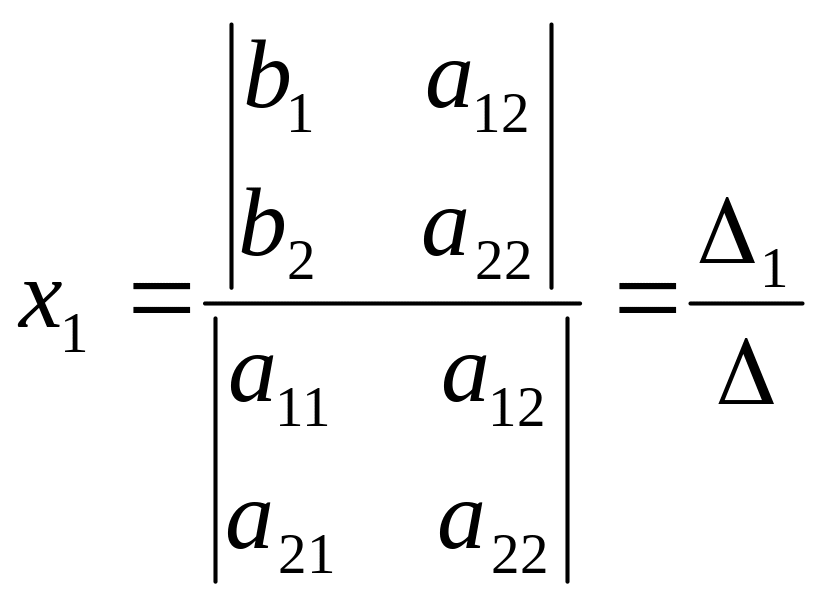Аналогично доказывается, что
.
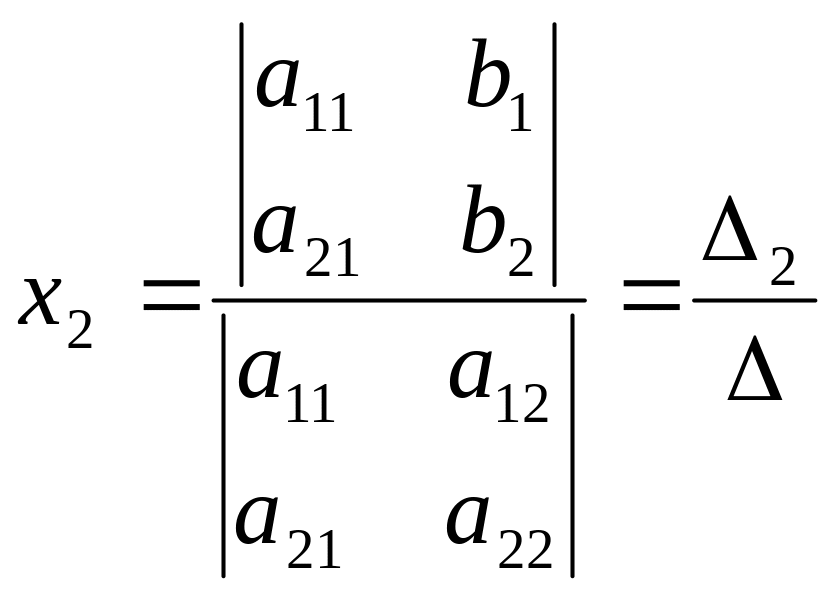Формулы 1.3. называют формулами Крамера (Г. Крамер- швейцарский математика XVIII века).
Пример.
Решить систему
Решение: Матрица
системы имеет вид
.
Вычислим ее определитель:
система имеет единственное решение.
Вычислим
По теореме получаем,
Ответ:
Пример.
Решить систему
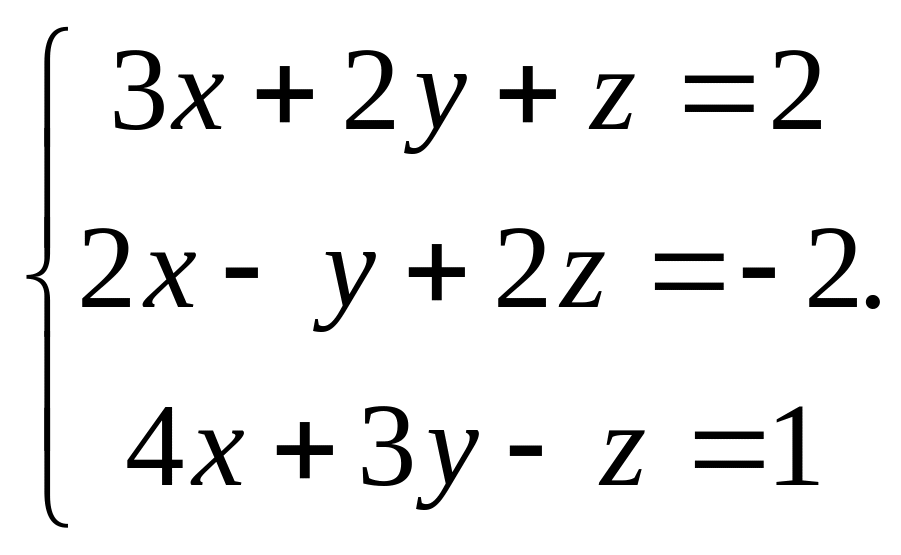
Решение. Матрица
системы имеет вид
.
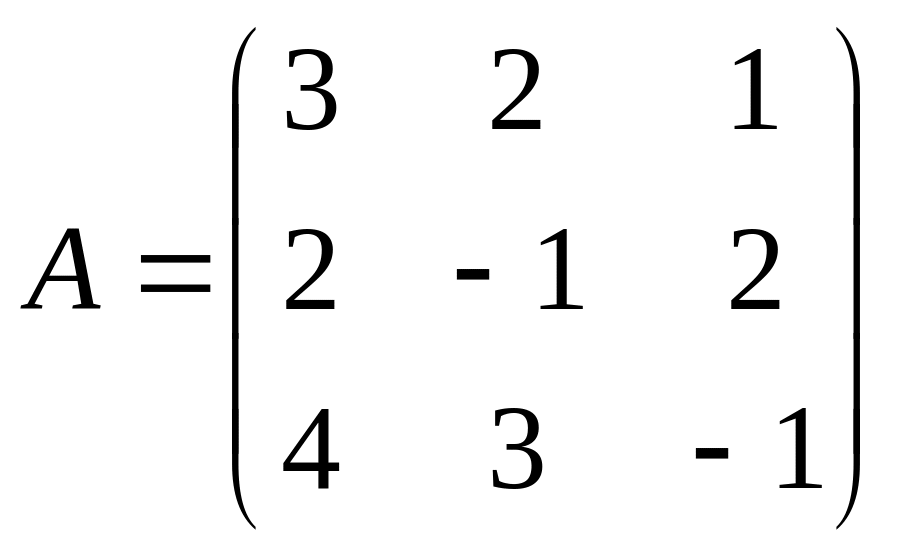Вычислим ее определитель, используя
разложение по 1-й строке:
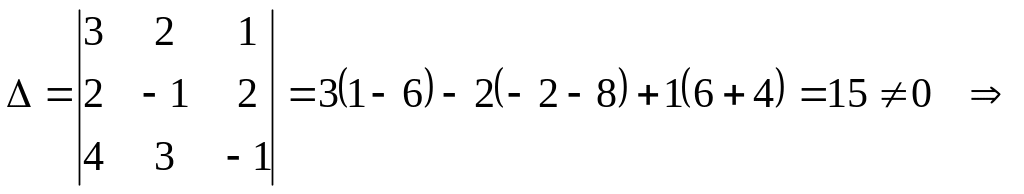система
имеет единственное решение. Вычислим
определители
с помощью разложения по 1-й строке:
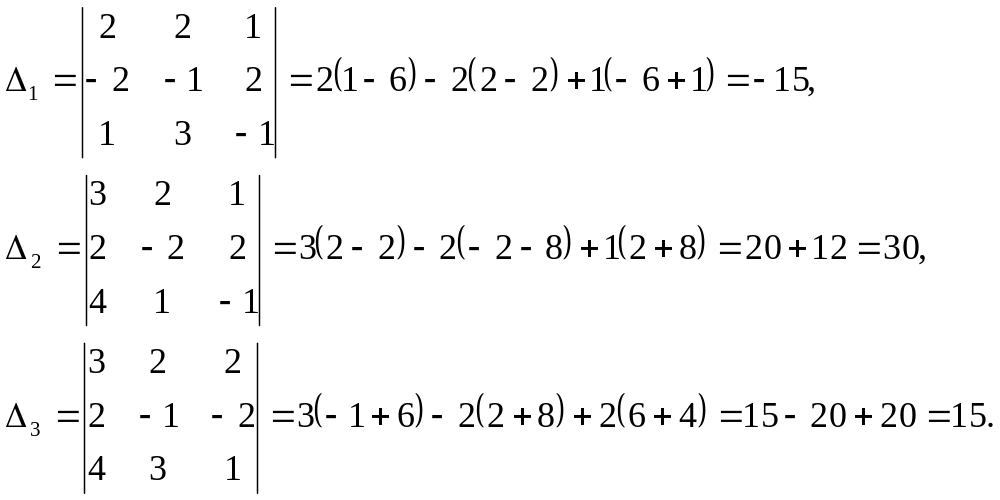
По теореме получаем,
Ответ:
Замечание. Справедливы следующие утверждения:
1. Если
и хотя бы один из
отличен
от нуля, то система не имеет решения;
2. Если
и все
,
то система либо не имеет решений, либо
имеет бесконечное множество решений.
Пример.
Решить СЛАУ методом Крамера
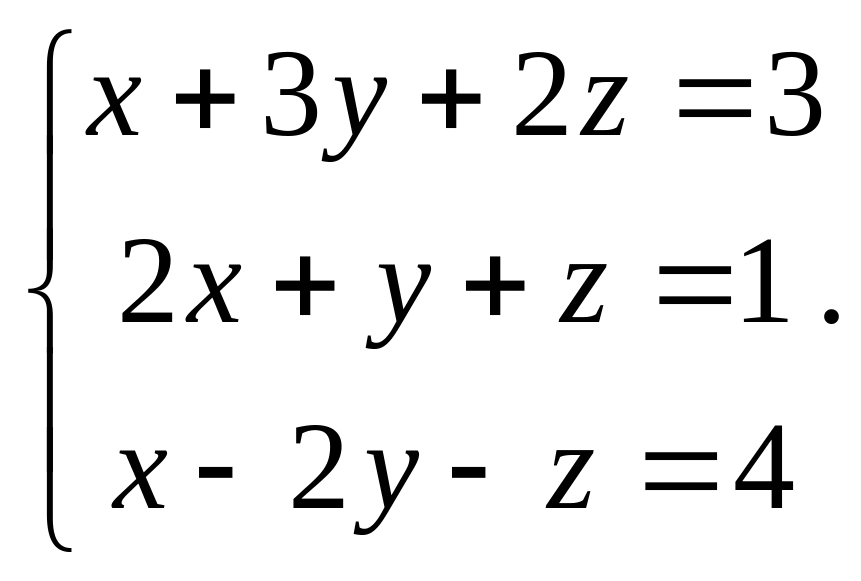
Решение. Вычислим определитель системы:
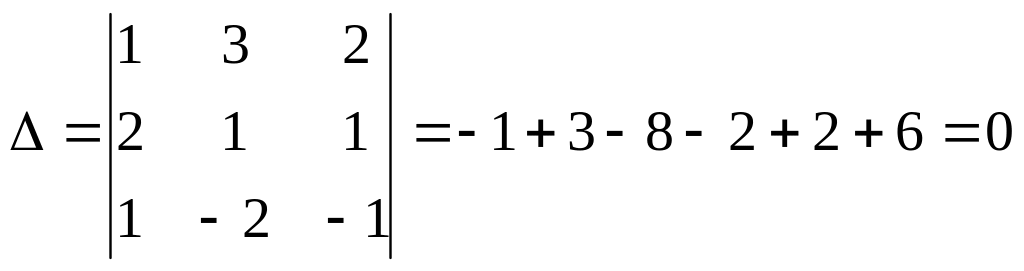Вычислим
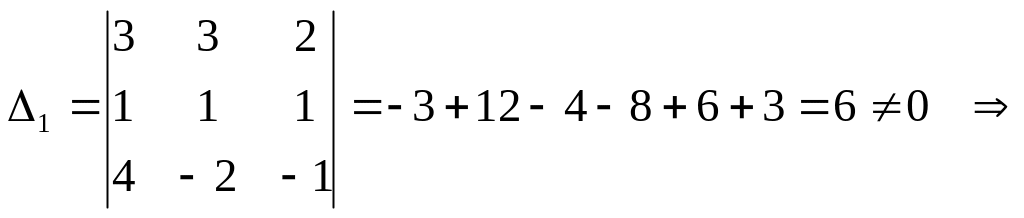система не имеет решений.
Контрольные задания.
1. Вычислить определители второго порядка
а)
2.
3.
Контрольные вопросы
1. Понятие системы линейных алгебраических уравнений (СЛАУ) m уравнений с n неизвестными. Решения СЛАУ.
2. Однородные и неоднородные СЛАУ.
3. Понятие совместной и несовместной СЛАУ. Совместная определенная система, совместная неопределенная система.
4. Понятие матрицы. Виды матриц: квадратные, матрица-строка, матрица-столбец, нулевая, диагональная, единичная,…..
Лекция 2.2.
Операции над матрицами. Решение систем матричным способом.
Время-2 часа
План:
1. Арифметические операции над матрицам.
2. Понятие обратной матрицы и метод ее нахождения.
3. Решение систем линейных алгебраических уравнений матричным методом.
Формулы Крамера не являются единственными формулами с помощью которых можно найти решение СЛАУ. Существует ряд других методов решений таких систем. В частности, СЛАУ может быть решена с помощью обратной матрицы. Для того, чтобы это понять необходимо разобраться с операциями, которые можно производить над матрицами.