1. Определение первообразной и неопределенного интеграла
Функция
называется первообразной
для функции
на некотором промежутке
,
если для любого
выполняется
равенство:
.
Из определения ясно, что функция должна быть непрерывна на всем промежутке и дифференцируема во всех внутренних точках данного промежутка.
Пример. Найти
первообразную для функции
.
Решение. Первообразной
будет функция
,
т.к.
.
Однако, первообразной будут и функции
и
и
,
которые отличаются только величиной
слагаемого. В силу того, что производная
постоянной равна нулю, имеем
.
Следовательно, любая функция вида
,
где С-
произвольная постоянная, будет
первообразной для данной функции.
Возникает вопрос:
исчерпывается ли множество всех
первообразных для данной функции
выражением вида
,
где
-одна
из первообразных, С-
произвольная постоянная.
Теорема 7.1.
(об общем виде первообразной)
Две различные первообразные
и
одной и той же функции
,
определенной на промежутке
,
отличаются друг от друга на постоянное
слагаемое, т.е.
Доказательство.
Пусть функция
и
являются первообразными для функции
.
Тогда выполняются равенства:
и
.
Рассмотрим производную разности
Тогда разность этих двух первообразных
тождественно равна константе, т.е.
.
Теорема доказана.
Геометрическая интерпретация теоремы.
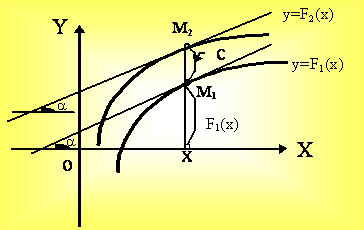
Эта теорема позволяет ввести понятие неопределенного интеграла.
Определение.
Неопределенным интегралом от функции
на промежутке
называется
совокупность всех первообразных для
функции
на этом промежутке и обозначается
символом
где
знак
интеграла;
подынтегральная
функция;
подынтегральное
выражение;
переменная
интегрирования;
Процесс нахождения неопределенного интеграла называется интегрированием.
Итак,
Возвращаясь к
рассмотренному примеру, можем записать
так
как
Приведем еще несколько примеров:
так
как
так
как
так как
С геометрической точки зрения неопределенный интеграл –это некоторое семейство кривых, отличающихся на постоянную величину. Каждая из этих кривых определяет одну из первообразных при фиксированном значении постоянной.
Свойства неопределенного интеграла
Будем считать, что все рассматриваемые функции определены на промежутке , функция непрерывна на и дифференцируема во всех внутренних точках .
1. Производная от
неопределенного интеграла равна
подыитегральной функции, т.е.
Доказательство.
2. Дифференциал от
неопределенного интеграла равен
подынтегральному выражению, т.е.
Доказательство.
По определению дифференциала имеем:
3. Интеграл от
дифференциала некоторой функции равен
сумме этой функции и произвольной
постоянной, т.е.
Доказательство.
По определению дифференциала и
определению неопределенного интеграла
имеем
4. Неопределенный
интеграл от алгебраической суммы функций
равен алгебраической суме интегралов
от слагаемых, т.е. (для двух функций)
Доказательство.
Пусть
и
.
Тогда
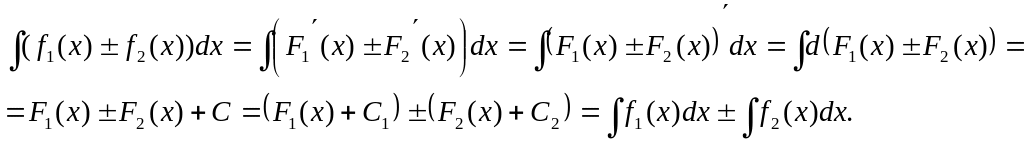
5. Постоянный
множитель можно выносить за знак
интеграла, т.е. для
выполнено
Доказательство.
По свойству
имеем
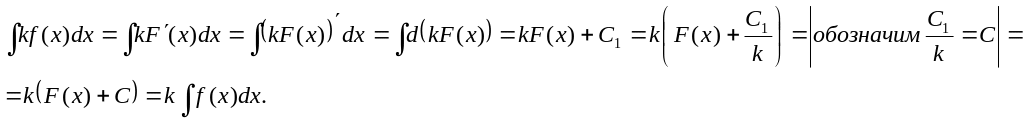
6. Если
то
где
произвольная
дифференцируемая функция. Это свойство
называется свойство
инвариантности формул интегрирования.