
- •Введение в предмет
- •Лекция 1.1.
- •Математика, ее история, основные элементы и методы
- •1. Предмет, задачи и содержание курса «Математика»
- •2. История развития математики, ее основные этапы
- •3. Развитие понятия числа. Комплексные числа.
- •Контрольные вопросы
- •Раздел I.
- •Тема 2.
- •1. Понятие системы линейных алгебраических уравнений
- •2. Понятие матрицы, виды матриц
- •3. Определители и их свойства. Формулы Крамера
- •1. Арифметические операции над матрицам
- •1)Сложение матриц
- •2) Вычитание матриц
- •3)Умножение матрицы на число
- •4) Произведение матриц
- •2. Понятие обратной матрицы и метод ее нахождения
- •3. Решение систем линейных алгебраических уравнений матричным методом
- •2. Метод Гаусса решения слау
- •Контрольные вопросы
- •Тема 3.
- •Элементы векторной алгебры и аналитической геометрии
- •Лекция 3.1.
- •Вектора
- •1. Вектор. Линейные операции над геометрическими векторами
- •Проекция вектора на ось. Разложение вектора по ортам координатных осей
- •Действия над векторами в координатной форме
- •Лекция 3.2. Нелинейные операции над векторами. Линейная независимость векторов и базис пространства.
- •2. Линейная зависимость и линейная независимость векторов Лекция 3.3 Аналитическая геометрия на плоскости и а пространстве
- •1. Метод координат на плоскости
- •2. Виды уравнений прямой на плоскости
- •3. Условия параллельности и перпендикулярности прямых на плоскости
- •4. Прямая и плоскость в пространстве
- •Контрольные вопросы
- •Раздел II.
- •Тема 4.
- •1. Множества и операции над ними
- •2. Понятие функции, ее свойства
- •3. Понятие числовой последовательности
- •Лекция 4.2. Предел функции, основные свойства
- •1. Предел числовой последовательности и его свойства
- •2. Понятие предела функции
- •3. Основные теоремы о пределах
- •Лекция 4.3. Бесконечно малые и бесконечно большие функции, их свойства
- •1. Понятие бесконечно малых и бесконечно больших функции, их свойства
- •2. Эквивалентные бесконечно малые функции
- •Раскрытие неопределенностей
- •Лекция 4.4. Замечательные пределы. Непрерывность функций
- •1. Первый замечательный предел
- •Второй замечательный предел
- •Непрерывные функции и их свойства
- •Контрольные вопросы
- •Тема 5.
- •Задачи, приводящие к понятию производной
- •Понятие смысл производной
- •Лекция 5.2. Понятие дифференциала функции и его применение в приближенных вычислениях
- •1. Понятие дифференциала функции, его свойства и геометрический смысл
- •2. Применение дифференциала в приближенных вычислениях
- •Лекция 6.3 Приложение понятия производной
- •Основные теоремы о дифференцируемых функциях
- •Применение производных для вычисления пределов функций (правило Лопиталя)
- •Задания для самостоятельной работы
- •Возрастание и убывание функций. Экстремумы функции
- •Лекция 5.4. Общее исследование функций с помощью производной
- •Контрольные вопросы
- •Тема 6.
- •Дифференциальное исчисление функции нескольких переменных
- •Лекция 6.1.
- •Фнп. Частные производные
- •1.Понятие функции двух и нескольких переменных
- •Лекция 6.2. Приложения понятия частных производных
- •Производная по направлению
- •2. Градиент функции и его применение
- •1. Определение первообразной и неопределенного интеграла
- •2. Непосредственное интегрирование
- •3. Основные методы интегрирования
- •Лекция 7.2. Определенный интеграл и его вычисление
- •Задача о площади криволинейной трапеции
- •Понятие определенного интеграла и его свойства
- •3.Формула Ньютона-Лейбница и основные методы нахождения определенного интеграла
- •Лекция 7.3. Определенный интеграл и его вычисление
- •Понятие несобственного интеграла второго рода
- •Приложения определенного интеграла
- •Контрольные вопросы по теме
- •Тема 8.
- •Дифференциальные уравнения
- •Лекция 8.1.
- •Дифференциальные уравнения первого порядка, их виды и методы решения
- •1. Понятие дифференциального уравнения и его решения
- •2. Дифференциальное уравнение первого порядка. Задача Коши
- •3. Основные виды дифференциальных уравнений первого порядка
- •Лекция 8.2. Дифференциальные уравнения высших порядков
- •1. Дифференциальные уравнения второго порядка, допускающие понижения порядка
- •2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные дифференциальные уравнения (лоду) второго порядка с постоянными коэффициентами
- •1. Понятие числового ряда, его сходимость и сумма
- •1.2. Примеры числовых рядов.
- •Лекция 9.2. Степенной ряд и его область сходимости.
- •2. Степенной ряд, вид его области сходимости
- •Контрольные вопросы
2. Понятие предела функции
Существует несколько равносильных определений предела функции.
Понятие окрестности точки
Рассмотрим
некоторую точку
![]() и произвольное число
и произвольное число
![]() .
Отметим на оси Ox
точку
и вправо и влево от нее отложим отрезки
длиной
.
Отметим на оси Ox
точку
и вправо и влево от нее отложим отрезки
длиной
![]() Нетрудно сообразить, что концы интервала
будут иметь значения
Нетрудно сообразить, что концы интервала
будут иметь значения
![]() и
и
![]() .
Получим промежуток с центром в точке
и диной
.
Получим промежуток с центром в точке
и диной
![]()
![]() окрестностью
точки
называют открытый промежуток
окрестностью
точки
называют открытый промежуток
![]() с центром в точке
.
с центром в точке
.
Если
![]()
![]() ,
то
,
то
![]()
или
![]()
или
![]() .
.
Так как у функции две переменные (независимая x и зависимая y), то дадим аналогичное определение окрестности для некоторой точки А, расположенной на оси Oy.
Рассмотрим
некоторую точку А
и произвольное
число
.
Отметим на оси Oy
точку A
и вправо и влево от нее отложим отрезки
длиной
![]() Нетрудно сообразить, что концы интервала
будут иметь значения
Нетрудно сообразить, что концы интервала
будут иметь значения
![]() и
и
![]() .
Получим промежуток с центром в точке A
и диной
.
Получим промежуток с центром в точке A
и диной
![]()
![]() окрестностью
точки А
называют открытый промежуток
окрестностью
точки А
называют открытый промежуток
![]() с центром в точке А.
с центром в точке А.
Определение предела функции в точке
Пусть функция определена в некоторой окрестности точки , везде, кроме, может быть, самой точки .
Число А
называется пределом
функции
при стремлении x
к
![]() ,
если для любого
существует такое
,
что для всех x
из
окрестности
точки
,
если для любого
существует такое
,
что для всех x
из
окрестности
точки
![]() соответствующие значения функции
соответствующие значения функции
![]() содержаться в
окрестности
точки А.
содержаться в
окрестности
точки А.
Предел функции
обозначается:
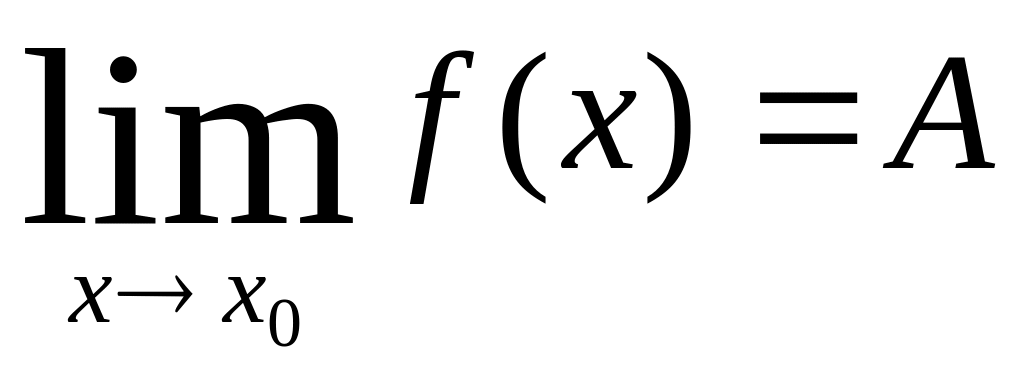 .
.
На языке
![]() определение предела функции может быть
записано следующим образом:
определение предела функции может быть
записано следующим образом:
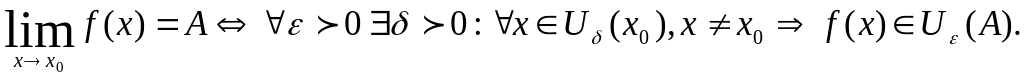
Геометрическая интерпретация предела функции.
Отметим на оси Oy
число А,
а на оси Ox
число
,
выделим
окрестность
точки А.
График функции
пересекает прямые
![]() ,
при этом проекции точек пересечения на
ось Ox
есть
и
.
Выберем в качестве
,
при этом проекции точек пересечения на
ось Ox
есть
и
.
Выберем в качестве
![]() меньшую из разностей
меньшую из разностей
![]() и
и
![]() .
В нашем случае,
.
В нашем случае,
![]() .
.
Рис.
Нетрудно видеть,
что если взять любое x
из окрестности
![]() ,
то существующее значение
обязательно будет принадлежать
окрестности
,
то существующее значение
обязательно будет принадлежать
окрестности
![]() .
.
Замечание 1.
В определении предела функции не
требуется существование функции в самой
точке
.
Значит, наличие или отсутствие предела
при
![]() определяется поведение функции в
окрестности точки
.
определяется поведение функции в
окрестности точки
.
Замечание 2.
Если при
переменная x
принимает лишь значения, меньшие
,
или наоборот, лишь большие
,
и при этом функция
стремиться к числу А,
то говорят об односторонних пределах
функции соответственно слева
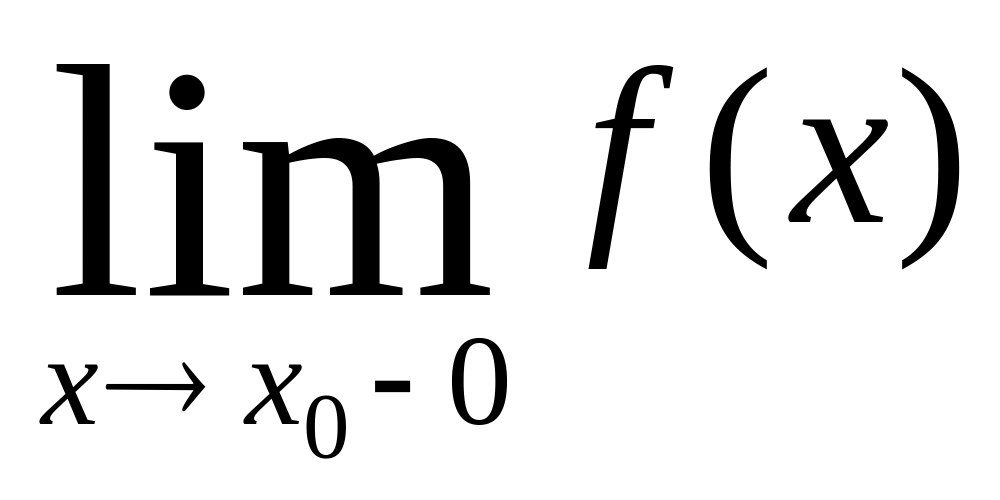 и справа
и справа
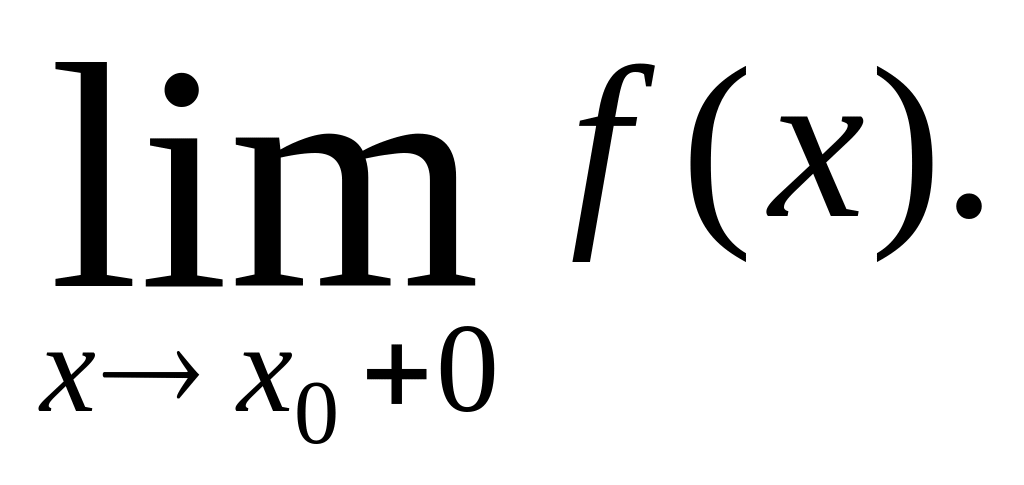
Замечание 3.
Не для всякой функции
существует предел
.
Например, функция
![]() не имеет предела при
не имеет предела при
![]() ,
т.к. ее значения при
колеблются между числами
,
т.к. ее значения при
колеблются между числами
![]() .
.
Для получения теоретических результатов и для нахождения пределов функций укажем несколько основных теорем.
3. Основные теоремы о пределах
Теорема 4.8. Функция может иметь только один предел при .
Теорема 4.9.
Предел постоянной величины равен самой
этой величине, т.е.
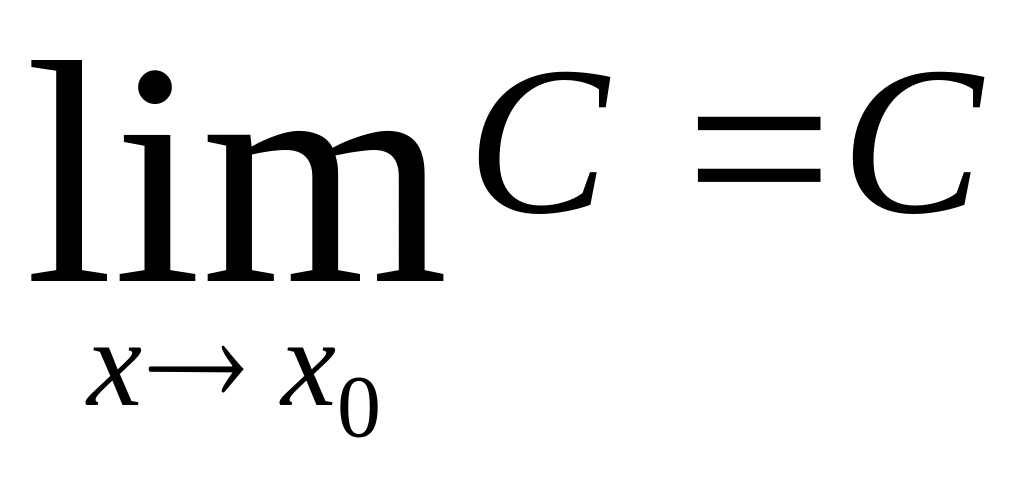 ,
где С-const.
,
где С-const.
Теорема 4.10. (о
пределе суммы, произведения и частного).
Пусть f(x)
и g(x)-функции,
для которых существуют конечные пределы:
и
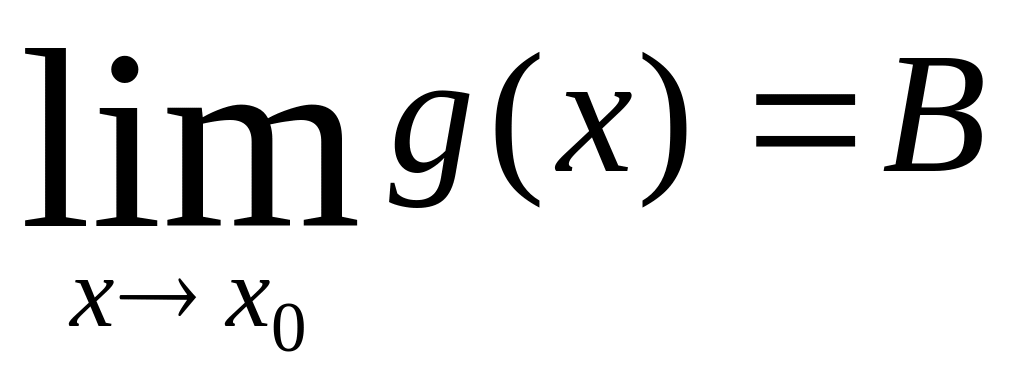 .
Тогда имеют место формулы:
.
Тогда имеют место формулы:
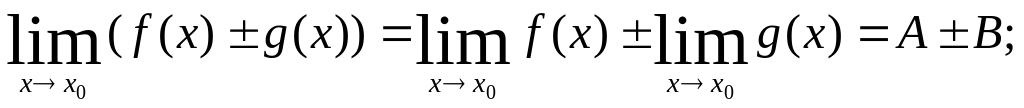 (4.1.)
(4.1.)
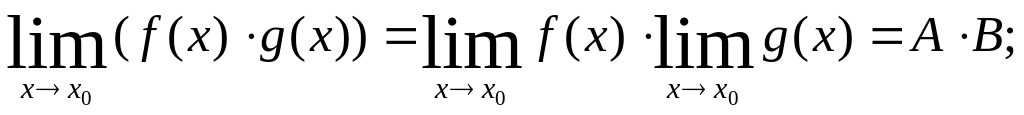 (4.2)
(4.2)
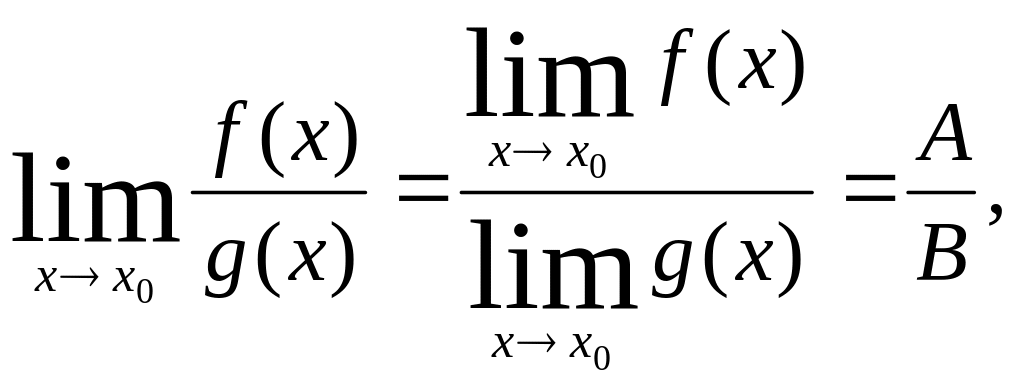 если
если
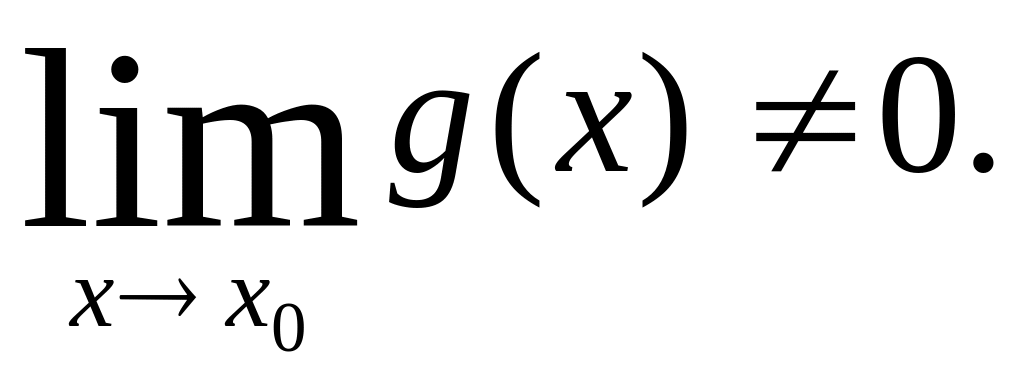 (4.3)
(4.3)
Замечание.
Обратное
неверно, т.е. из существования предела
суммы, произведения или частного функций
не следует существование пределов самих
слагаемых, сомножителей или делителя
и делимого. Например,
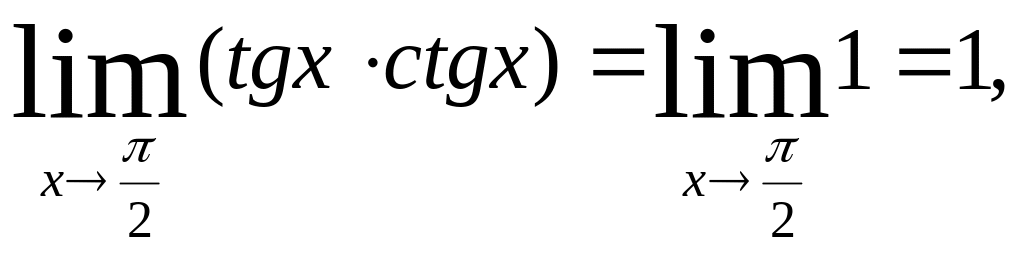 но отсюда совсем не следует существование
пределов
но отсюда совсем не следует существование
пределов
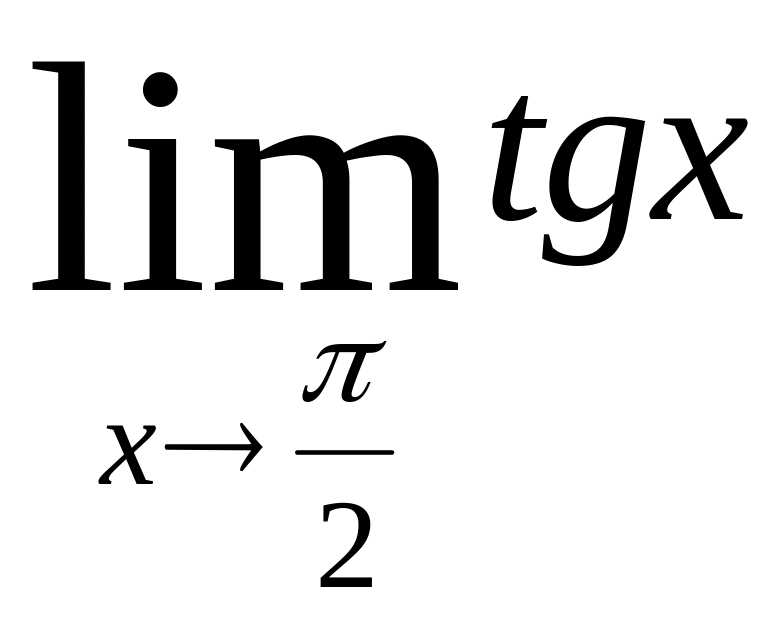 и
и
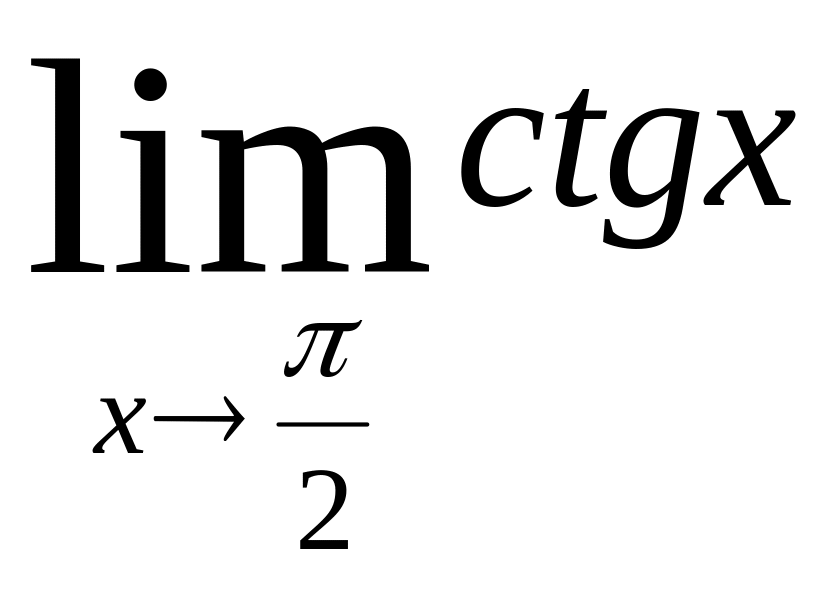 .
(Первый предел не существует).
.
(Первый предел не существует).
Следствие 1. Формулы (4.1) и (4.2) справедливы для любого конечного числа слагаемых и множителей соответственно.
Следствие 2. Из формулы (4.2) и теоремы (4.9) следует, что постоянный множитель можно выносить за знак предела, т.е.
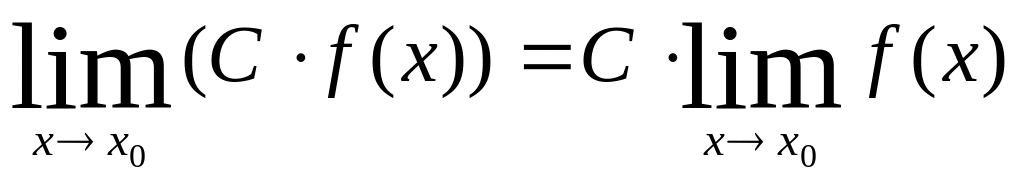
Следствие 3. Предел степени равен степени предела, т.е.
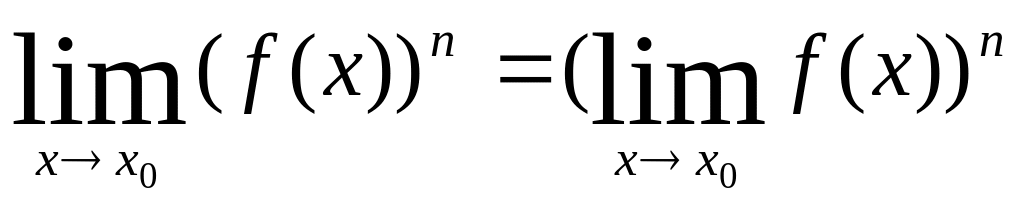
Если в формуле (4.2) предположить, что перемножается одна и та же функция несколько раз, то получим это равенство.
.
Пример 4.2. Найти
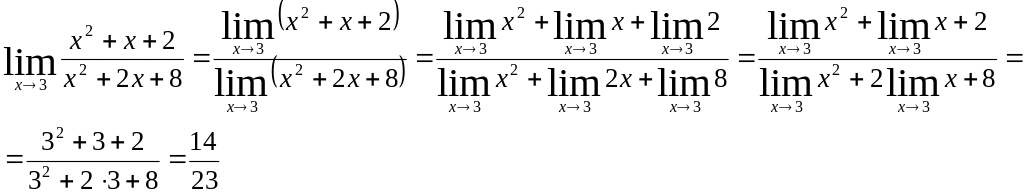
Итак, решение предела свелось к обычной подстановке предельного значения аргумента в функцию, стоящую под знаком предела, т.е. вместо x подставили число 3. Такой способ вычисления предела функции применим, если точка входит в область определения функции.
Теорема 4.11.
Если

Не всякий предел
можно найти так просто. Иногда при
вычислении пределов результат формальной
подстановки в функцию предельного
значения аргумента приводит к выражения
вида
![]() и теоремы о пределах функций оставляют
без внимания эти случаи. В этих случаях
говорят, что имеет место неопределенность,
а найти предел означает- раскрыть эту
неопределенность. Существуют определенные
методы для раскрытия неопределенностей,
при этом важную роль играют функции,
пределы которых раны либо нулю, либо
бесконечности.
и теоремы о пределах функций оставляют
без внимания эти случаи. В этих случаях
говорят, что имеет место неопределенность,
а найти предел означает- раскрыть эту
неопределенность. Существуют определенные
методы для раскрытия неопределенностей,
при этом важную роль играют функции,
пределы которых раны либо нулю, либо
бесконечности.
