2. История развития математики, ее основные этапы

Академик А.Н. Колмогоров выделяет четыре этапа развития математики:

1) период зарождения математики;

2) период элементарной математики, начинающийся в VI-V вв. до н.э. и завершающийся в конце XVI в. ("Запас понятий, с которыми имела дело математика до начала XVII в., составляет и до настоящего времени основу «элементарной математики», преподаваемой в начальной и средней школе")

3) период математики переменных величин, охватывающий XVII-XVIII вв., "который можно условно назвать также периодом «высшей математики»";

4) период современной математики - математики XIX-XX вв., в ходе которого математикам пришлось "отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм".

3. Развитие понятия числа. Комплексные числа.

Число — абстракция, используемая для количественной характеристики объектов. Письменными знаками (символами) для записи чисел служат цифры. В математике выделяют- натуральные N, целые Z, рациональные Q, иррациональные I, действительные R и комплексные числа C.

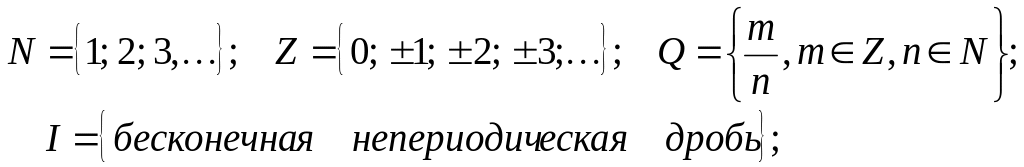
Например, числа рациональные, а числа иррациональные. Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел, т.е. Очевидно, что

Множество действительных чисел R дополняют двумя элементами, обозначаемыми и (плюс и минус бесконечность). При этом полагают, что

Но операции не определены.

В современной математике помимо действительных чисел используются комплексные числа. Они возникли в связи с решением алгебраических уравнений третьей степени в так называемом неприводимом случае, когда действительные корни выражаются через кубические корни из мнимых величин (формула для нахождения корней кубического уравнения вида открытая Д. Карадано и Р. Бомбелли в XVI веке имела вид: ). Необходимо отметить, что процесс становления комплексных чисел был долгим. Это связано с тем, что для квадратных уравнений нет необходимости искать корни в случае отрицательного дискриминанта, потому, что корни такого уравнения не имеют физического смысла.

Пример. Найти квадрат, площадь которого на 6 единиц меньше полусуммы всех его сторон.

Решение. Пусть x- сторона квадрата; -площадь квадрата; 2x-полусумма его сторон. Из условия задачи имеем:

или . Уравнение решений не имеет, т.к. Значит, такого квадрата не существует.

Совсем другая ситуация имеет место в случае уравнения третьей степени.

Пример. Найти размер куба, объем которого на 6 единиц меньше суммы семи его ребер.

Решение. Пусть x- сторона куба; x³ -объем куба; 7x-сумма семи его ребер. Из условия задачи имеем:

или

Решим данное уравнение:

1 способ:	2 способ:
- корень уравнения (подбор) Целая часть x в квадрате остаток кв. уравнение с корнями -3 и 2 Итак, решением данного уравнения являются числа: Таким, образом, куб с описанным свойством существует.	Используем формулу для корней кубического уравнения при Под знаком квадратного корня оказалось отрицательное число. Получается, что путь к корням идет через невозможную операцию извлечения квадратного корня из отрицательного числа.

Так как задача имеет реальное решение, то появляется необходимость как-то определить корень из отрицательного числа, а именно определить величину . Новые числа, для которых определили величину , назвали комплексными. Комплексные числа появились в XVI веке при решении уравнений третьей степени, когда стало ясно, что реальные решения уравнений существуют, но не могут быть найдены действиями над действительными числами.

Понятие комплексного числа, его алгебраическая форма

Комплексным числом z называется выражение вида где x и y-действительные числа, а i- мнимая единица,

Число x называется действительной частью комплексного числа z и обозначается (от французского reele-действительный), а число y- мнимой частью комплексного числа z и обозначается (от французского imaginaire- мнимый).

Если , то число называется чисто мнимым; если , то число превращается в действительное число. Множество всех комплексных чисел обозначается C. Из вышесказанного ясно, что множество всех действительных чисел является подмножеством комплексных чисел, т.е.  

Два комплексных числа и называются равными, если и . Понятие «больше» и «меньше» для комплексного числа не вводят.

Два комплексных числа и отличающиеся лишь знаком мнимой части, называются сопряженными.

Выражение называют алгебраической формой комплексного числа.

Арифметические действия над комплексными числами

1. Сложение комплексных чисел

Суммой комплексных чисел и называется комплексное число, определяемое равенством .

2. Вычитание комплексных чисел

Разностью комплексных чисел и называется комплексное число, определяемое равенством .

Теорема 1.1. Сумма двух сопряженных комплексных чисел является действительным числом, а разность - чисто мнимым.

Доказательство. Найдем сумму и разность двух сопряженных чисел:

Вино, что первое число является действительным, а второе- чисто мнимым.

3. Умножение комплексных чисел

Произведением комплексных чисел и называется комплексное число, определяемое равенством

Эту формулу можно получить, если перемножить комплексные числа, как многочлены и учесть, что

Теорема 1.2. Произведение двух сопряженных комплексных чисел является действительным числом, равным сумме квадратов действительной и мнимой частей.

Доказательство. Найдем произведение двух сопряженных чисел:

4. Деление комплексных чисел

Частным двух комплексных чисел и называется комплексное число, определяемое равенством

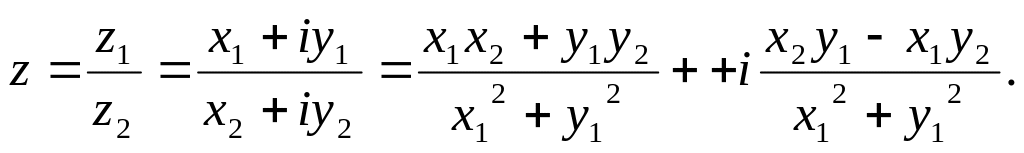
Данная формула может быть получена домножением числителя и знаменателя на число, сопряженное знаменателю:

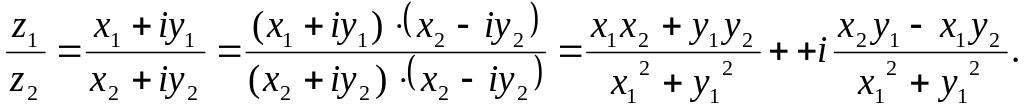
Пример 1.1. Даны Найти:

Решение:

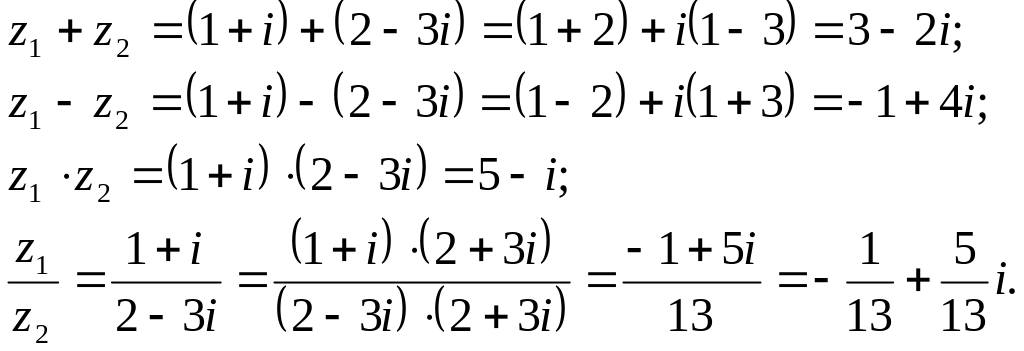
Тригонометрическая форма комплексного числа

Всякое комплексное число можно изобразить на плоскости. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, а ось ординат- мнимой осью.

Комплексное число можно задать с помощью радиус-вектора , начало которого в точке , а конец в точке

Длина вектора называется модулем комплексного числа и обозначается или Величина угла между положительным направлением действительной оси и вектором называется аргументом этого комплексного числа и обозначается или Аргумент комплексного числа величина многозначная и определяется с точностью до Значение аргумента, заключенное в промежутке ( , обозначается и называется главным значением аргумента. Очевидно, что

Определим еще одну форму комплексного числа –тригонометрическую.

……..