Миноры и алгебраические дополнения

Рассмотрим определитель третьего порядка, применив новую систему обозначений элементов с помощью двойных индексов. Первый индекс в обозначении элемента условимся считать номером строки, а второй – номером столбца, на пересечении которых находится данный элемент.

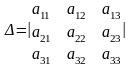
Введем понятие минора и алгебраического дополнения элемента определителя.

Определение: Минором элемента определителя 3-его порядка называется определитель 2-го порядка, полученный из данного вычеркиванием той строки и того столбца, на пересечении которых находится данный элемент.

Так, например, минором элемент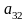а определителя 3-его порядка будет определитель 2-го порядка.

;

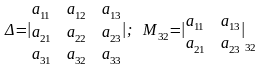Обозначается

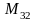
Определение: Алгебраическим дополнением элемента называется минор, взятый со знаком «+», если сумма номеров вычеркиваемых строк и столбцов есть четное число и со знаком «-», если эта сумма – нечетное число.

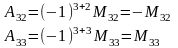
Определители высших порядков, их вычисление.

Определителем n-го порядка называется определитель вида: 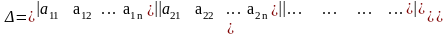, который вычисляется путем разложения по элементам любой строки (столбца).

Теорема о разложении определителя

Теорема: Сумма произведений элементов какой-либо строки (или столбца) на соответствующие алгебраические дополнения элементов той же строки равна величине определителя.

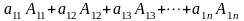
По аналогии можно вычислить определитель n-го порядка, разложив его по элементам какой-либо строки или столбца, и его вычисление сводится к вычислению определителей 3-его порядка.

Вычисление определителей n-го порядка сводится к выполнению определителей (n – 1) порядка.

Лекция №2. Тема: «Матрицы, матричный метод решения слу».

Матрицей размера mn называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

A =

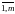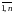или сокращенно в виде A = (a_{i j}) (i = ; j = ). Числа a_{i j}, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй – на номер столбца. Две матрицы A = (a_{i j}) и B = (b_{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_{i j} = b_{i j}.

Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

Виды матриц.

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера mn, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0.

Элементы матрицы с одинаковыми индексами называют элементами главной диагонали.

Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n.

Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

Если все элементы a_{i i} диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

E = .

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю.

Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

A^T = ,

которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.