Дифференциальные уравнения первого порядка.
Дифференциальные уравнения первого порядка имеют вид
.
Если это уравнение можно разрешить
относительно
,
то его можно записать
.
В этом случае мы говорим, что дифференциальное
уравнение разрешено относительно
производной. Для такого уравнения
справедлива следующая теорема, которая
называется теоремой о существовании и
единственности решения дифференциального
уравнения.
Теорема. Если в уравнении
функция
и
ее частная производная
по
непрерывны
в некоторой области
на
плоскости
,
содержащей некоторую точку
,
то существует единственное решение
этого уравнения
,
удовлетворяющее условию:
при
.
Геометрический смысл теоремы заключается в том, что существует и при том единственная функция , график которой проходит через точку .
Условие, что при
функция
должна
равняться заданному числу
,
называется начальным условием. Оно
записывается в виде
.
Дадим геометрическую интерпретацию дифференциального уравнения первого порядка.
Пусть дано дифференциальное уравнение,
разрешенное относительно производной
(*)
и пусть
-
есть общее решение данного уравнения.
Это общее решение определяет семейство
интегральных кривых на плоскости
.
Уравнение (*) для каждой точки
с
координатами
и
определяет
значение производной
,
т.е. угловой коэффициент касательной к
интегральной кривой, проходящей через
эту точку. Таким образом, дифференциальное
уравнение (*) дает совокупность направлений
или, как говорят, определяет поле
направлений на плоскости
.
Следующая, с геометрической точки зрения задача интегрирования дифференциального уравнения заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля в соответствующих точках.
Для дифференциального уравнения (*)
геометрическое место точек, в которых
выполняется соотношение
,
называется изоклиной данного
дифференциального уравнения.
Дано: у = f(Х;У)- обыкновенное дифференциальное уравнение 1- ого порядка
f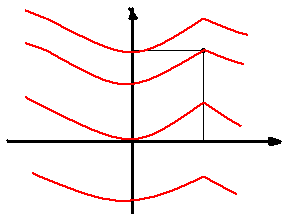
(х
;у ) = у(х) = tg - угол наклона
(х;у) = (2;1) f(х;у) = 1= tg 45°
(х;у)= (3;2) f(х;у) = -1= tg 135°
(х;у) = (5;7) f(х;у) = √3 = tg60°
Задано дифференциальное уравнение 1-го порядка - означает, что поле векторов касательно к искомой кривой.
Найти решение обыкновенного дифференциального уравнения 1-го порядка означает восстановить или найти кривую по данному полю векторов.
Решение дифференциальных уравнений - это класс, семейство кривых удовлетворяющих следующим требованиям:
1. При любом С (Х/С) будет решением дифференциального уравнения.
2. Для данного начального условия (Хо;Уо) Fс=Co ф(Х;Со) удовлетворяет данному начальному условию, т.е. f (х;Со): F(Хо;Со) = Уо
Семейство кривых У = f(Х;С) называется общим решением уравнения, если она удовлетворяет условия 1 и 2.
Определение: Частное решение –решение, которое удовлетворяет данному начальному условию (геометрически)-частное решение- это интегральная кривая из семейства проходящее через данную точку.
О
собые
применения
Общее решение
Определение: Решение называется особым, если: 1. это решение дифференциального уравнения 2. Оно не входит в общее решение.
Особое решение- это такое частное решение, которое не входит в общее решение.
Решение дифференциальных уравнений 1-го порядка.