
- •Западно-Казахстанский государственный университет им. М. Утемисова
- •Учебно-методический комплекс дисциплины «Математика для экономистов»
- •Курс – 1
- •Всего – 87 часов Уральск
- •Западно-Казахстанский государственный университет им. М. Утемисова
- •Программа курса (sillabus) «Математика для экономистов»
- •Курс – 1
- •Всего – 87 часов Уральск
- •1.1 Данные о преподавателе Садыкова г.А. – ст. Преподаватель
- •1.2 Данные о дисциплине Математика для экономистов
- •1.3 Введение
- •2. Программа обучения по дисциплине - syllabus
- •Кредит час 2
- •Кредит час 1 Лекция №5
- •Кредит час 3
- •Кредит час 3
- •Кредит час 1
- •Кредит час 2
- •Практическое занятие№ 8
- •Кредит час 1
- •Неделя 11 Кредит час 1
- •Кредит час 2
- •Кредит час 1
- •Кредит час 2
- •Лекция №25
- •Лекция №26
- •Лекция №27
- •3. График выполнения и сдачи заданий по дисциплине Математика для экономистов
- •4. Карта учебно-методической обеспеченности дисциплины
- •Лекционный комплекс:
- •Лекция №1. Тема: «Определители 2,3 порядков. Системы линейных уравнений. Метод Крамера».
- •Свойства определителей 3-го порядка
- •Системы линейных уравнений.
- •Правило Крамера.
- •Миноры и алгебраические дополнения
- •Определители высших порядков, их вычисление.
- •Теорема о разложении определителя
- •Лекция №2. Тема: «Матрицы, матричный метод решения слу».
- •Виды матриц.
- •Действие над матрицами.
- •Обратная матрица.
- •Матричный метод решения слу
- •Лекция №3. Тема: «Ранг матрицы. Метод Гаусса. Система m уравнений с n неизвестными».
- •Системы линейных уравнений.
- •Критерий совместности и единственности решения слу. Теорема Кронекера-Капелли.
- •Лекция №№ 4-7 Векторы, линейные операции над векторами. Линии первого порядка на плоскости.
- •4.1. Векторы. Основные понятия и простейшие действия над векторами. Базис и координаты.
- •4.2. Скалярное, векторное, смешанное произведение векторов. Свойства скалярного произведения.
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •4.3. Понятие об уравнении линии. Различные уравнения прямой.
- •Частные случаи общего уравнения прямой
- •Практические занятия к теме 2.
- •Контрольные вопросы и задания к теме 2.
- •Задачи к теме 2
- •Производная функции в точке. Таблица производных, правила дифференцирования. Дифференциал функции.
- •5.1. Механический, геометрический, экономический смысл производной.
- •5.2. Основные правила дифференцирования.
- •5.3. Производные высших порядков
- •5.4. Дифференциал.
- •5.5 .Геометрический смысл дифференциала.
- •Практические занятия к теме 5.
- •Контрольные вопросы и задания к теме 5.
- •Задания к теме 5.
- •Лекция №№ 15-17 Неопределенный интеграл.
- •7.1. Первообразная и неопределенный интеграл. Основные свойства.
- •Неопределенный интеграл представляет собой семейство функций
- •Из определения неопределенного интеграла следуют следующие свойства:
- •Методы интегрирования
- •7.2. Метод замены переменной.
- •7.3. Метод интегрирования по частям.
- •Проинтегрируем обе части
- •7.4. Интегрирование рациональных дробей.
- •7.5. Метод неопределенных коэффициентов в интегрировании рациональных дробей.
- •1 Случай.
- •2 Случай.
- •7.6. Интегрирование некоторых тригонометрических выражении.
- •7.7. Интегрирование некоторых видов иррациональностей.
- •Практические занятия к теме 8.
- •Контрольные вопросы и задания к теме 8.
- •Задания к теме 7. Вычислить интегралы:
- •Лекция №№ 19-20 Ряды. Числовой ряд. Сходимость и сумма числового ряда. Необходимое условие сходимости числового ряда.
- •Достаточные признаки сходимости: признаки Даламбера, Коши и другие.
- •10 Признак Даламбера.
- •20 Интегральный признак Коши.
- •4О. Признак сравнения.
- •Имеем ряд (2)
- •Функциональные ряды.
- •На основании признака Даламбера
- •Степенной ряд. Разложение функции в ряд Тейлора-Маклорена.
- •Ряд Фурье. Разложение функции в тригонометрический ряд Фурье.
- •Практические занятия к теме 11.
- •Контрольные вопросы и задания к теме 11.
- •Задания к теме 11.
- •Лекция №№ 21-24 Дифференциальные уравнения. Дифференциальные уравнения. Основные понятий, определения и уравнения с разделяющими переменными.
- •Дифференциальные уравнения первого порядка.
- •Уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения первого порядка.
- •Линейные дифференциальные уравнения первого порядка.
- •Уравнение Бернулли.
- •Линейные однородные дифференциальные уравненияс постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения II порядка с постоянными коэффициентами.
- •Системы обыкновенных дифференциальных уравнений.
- •Практические занятия к теме 10.
- •Контрольные вопросы и задания к теме 10.
- •Задания к теме 10.
- •6. Планы семинарских (практических) занятий, планы занятий в рамках срсп и срс
- •Семинар 2 Тема: Матрицы, матричный метод решения слу. Метод Гаусса.
- •Семинар- 3 Тема: « Векторы, линейные операции над векторами. Линии 1- го порядка на плоскости».
- •Семинар-6 (1 ч) Тема: Функции нескольких переменных.
- •Семинар 7 Тема: Интегральное исчисление. Неопределенный интеграл.
- •Семинар 8 Тема: Интегральное исчисление. Определенный интеграл.
- •2. Рассмотреть сходимость гармонического ряда.
- •Темы для самостоятельного изучения по дисциплине «Математика для экономистов»
- •Политика выставления оценки:
- •Знания, умения и навыки студентов оцениваются следующим образом:
- •Вопросы для проведения контроля знаний студентов по темам и экзамена
- •20. Даны координаты вершин треугольника авс
- •Примерный перечень тестовых вопросов для промежуточного и итогового контроля.
- •Примерные экзаменационные тестовые задания Вариант *
- •Список литературы
- •Дополнительная литература.
- •4. Глоссарий по дисциплине Математика для экономистов
Действие над матрицами.
Произведением матрицы А на число называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число : A = ( ai j).
Т.е. для того чтобы умножить матрицу A на число нужно каждый элемент матрицы A умножить на это число.
Суммой двух матриц А = (ai j) и B = (bi j) одного размера называется матрица C = (ci j) того же размера, элементы которой определяются по формуле ci j = ai j + bi j.
Т.е. чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Или:
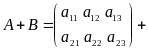
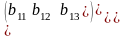 =
=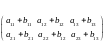
Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Произведением
двух матриц А = (ai j) и B = (bj k),
где i =
,
j=
,
k=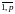 ,
заданных в определенном порядке АВ,
называется матрица С = (c i k), элементы
которой определяются по следующему
правилу:
,
заданных в определенном порядке АВ,
называется матрица С = (c i k), элементы
которой определяются по следующему
правилу:
c
i k = ai
1 b1 k
+ ai 2
b2 k
+… + ai m
bm k =
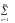 ai
s bs
k.
ai
s bs
k.
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Т.е. перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы.
Обратная матрица.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если = 0.
Понятие обратной матрицы вводится только для квадратных матриц.
Если A
– квадратная матрица, то обратной
для неё матрицей называется матрица,
обозначаемая A-1
и удовлетворяющая условию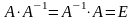 .
.
Справедлива следующая теорема:
Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.
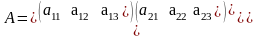
находится следующим образом

,
где Aij – алгебраические дополнения элементов aij данной матрицы A.
Итак, чтобы найти обратную матрицу нужно:
Найти определитель матрицы A.
Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу, элементами которой являются числа Aij.
Найти матрицу, транспонированную полученной матрице А, и умножить её на
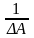 –
это и будет обратная матрица.
–
это и будет обратная матрица.
Аналогично для
матриц второго порядка, обратной будет
следующая матрица
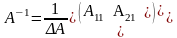 .
.
Матричный метод решения слу
Рассмотрим систему, состоящую из n линейных уравнений с n неизвестными:
Вводя матрицу коэффициентов перед неизвестными А, матрицу-столбец неизвестных Х и матрицу-столбец свободных членов В, систему можно переписать в матричной форме:
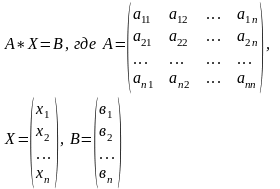
Предположим, что матрица А - неособенная, т.е. А ≠ 0. Решим матричное уравнение, а следовательно и систему (4) с помощью обратной матрицы А,
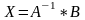 где, А =
где, А =
 * Ặ =>
* Ặ =>
X
=
* Ặ
=>
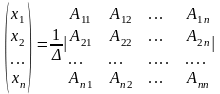
Для системы трех уравнений с тремя неизвестными:
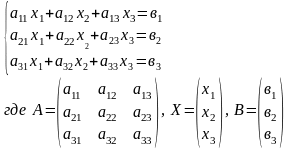
решение запишется в виде:
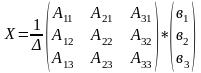
Лекция №3. Тема: «Ранг матрицы. Метод Гаусса. Система m уравнений с n неизвестными».
Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А.
Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим.
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A).
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A B.
